LeetCode Substring with Concatenation of All Words暴力法暴力法更加暴力的方法
Substring with Concatenation of All Words
You are given a string, S, and a list of words, L, that are all of the same length. Find all starting indices of substring(s) in S that is a concatenation of each word in L exactly once and without any intervening characters.
For example, given:
S: "barfoothefoobarman"
L: ["foo", "bar"]
You should return the indices: [0,9].
(order does not matter).
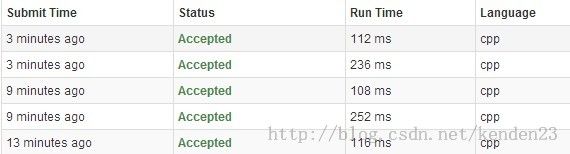
这里使用一种巧妙点的暴力法和一种原始的暴力法来解决这个问题。巧妙点的暴力法是参考了LeetCode上的,然后改进来的,时间上快了差不多一倍,有图有真相:
![]()
LeeCode上的代码都是200多ms,我下面的代码是100多ms。最后一个1632ms的是原始的暴力法。
主要思想是一样的,最主要的就是会如何分段例如:
三个字母一段 abc def ghi jk那么可以在分a bcd efg hij k还可以分ab cde fgh ijk然后再分就重复了。
所以三个字母分为一段的只有三种分法,同样道理四个字母的只有四种分法。
懂得这个思想就能写出比原始的暴力法快出10倍多的程序了。
我的代码改进的地方主要是:
当检测到有一个单词不相等的时候,如果后面的主串的字母数剩下小于lLen*len(L中的单词数和每个单词的字母数的乘积),那么就不用继续比较了。
LeetCode上的还把map换成了vector,以方便查找,不过感觉也没有这个必要。
下面是我的程序:
vector<int> findSubstring(string S, vector<string> &L)
{
int sLen = S.length();
int lLen = L.size();
if (lLen < 1) return vector<int>();
int len = L[0].length();
vector<int> res;
map<string, int> LMap;
map<string, int> countMap;
string index;
for (auto x: L)
LMap[x]++;
//熟记这个思维,巧妙地分段
for (int d = 0; d < len; d++)
{
//注意:是i=d不是i=0;
for (int i = d; i <= sLen-lLen*len; i += len)
{
int start = i;
index = S.substr(i,len);
//注意:后面的是i<=sLen-len不是sLen-lLen*len
while (LMap.count(index) > 0 && i <= sLen-len)
{
countMap[index]++;
//这里就不能用map的count函数了,因为count只会返回0或1
//一定要熟悉STL函数的各种用法,否则会出错。
//这个函数把握不好,结果浪费大量的时间。
//本题卡的最长时间的是这个小小的函数和程序结构开始没写好
if (countMap[index] > LMap[index])
{
string sTemp = S.substr(start,len);
while (sTemp != index)
{
start += len;
sTemp = S.substr(start,len);
//每前进一步,减少一个相等元素
countMap[sTemp]--;
}
countMap[index]--;
start += len;
}
i+=len;
if ((i-start)/len == lLen)
{
res.push_back(start);
string sTemp = S.substr(start, len);
countMap[sTemp]--;
start+=len;
}
index = S.substr(i,len);
}
countMap.clear();
}
}
return res;
}
下面是LeetCode上的不错的程序:
http://discuss.leetcode.com/questions/210/substring-with-concatenation-of-all-words
class Solution {
public:
vector<int> findSubstring(string S, vector<string> &L) {
// Start typing your C/C++ solution below
// DO NOT write int main() function
int m = S.size(), n = L.size(), len = L[0].size();
map<string, int> ids;
vector<int> need(n, 0);
for (int i = 0; i < n; ++i) {
if (!ids.count(L[i])) ids[L[i]] = i;
need[ids[L[i]]]++;
}
vector<int> s(m, -1);
for (int i = 0; i < m - len + 1; ++i) {
string key = S.substr(i, len);
s[i] = ids.count(key) ? ids[key] : -1;
}
vector<int> ret;
for (int offset = 0; offset < len; ++offset) {
vector<int> found(n, 0);
int count = 0, begin = offset;
for (int i = offset; i < m - len + 1; i += len) {
if (s[i] < 0) {
// recount
begin = i + len;
count = 0;
found.clear();
found.resize(n, 0);
} else {
int id = s[i];
found[id]++;
if (need[id] && found[id] <= need[id])
count++;
if (count == n)
ret.push_back(begin);
// move current window
if ((i - begin) / len + 1 == n) {
id = s[begin];
if (need[id] && found[id] == need[id])
count--;
found[id]--;
begin += len;
}
}
}
}
return ret;
}
};
最后是原始暴力法,很暴力,速度比上面的慢上10多倍,有图:
![]()
实际运行也许更加慢,我在自己的电脑上测试一个很大的数据,前面的方法一下出来了,这个原始的暴力法需要等上6到7秒多。不过胜在它的方法很原始很简单,处理的情况也比较简单。不过太慢了,虽然Accepted了,但是感觉还是不实用的。
vector<int> findSubstring(string &S, vector<string> &L)
{
int sLen = S.length();
int lLen = L.size();
if (lLen < 1) return vector<int>();
int len = L[0].length();
vector<int> res;
map<string, int> LMap;
map<string, int> countMap;
string index;
for (auto x: L)
LMap[x]++;
for(int i = 0; i <= S.size()-lLen*len; ++i)
{
countMap.clear();
int j = 0;
for(j = 0; j < lLen; ++j)
{
string index = S.substr(i+j*len, len);
if(LMap.find(index) == LMap.end())
break;
++countMap[index];
if(countMap[index] > LMap[index])
break;
}
if(j == lLen) res.push_back(i);
}
return res;
}
//2014-1-25
class Solution3 {
public:
vector<int> findSubstring(string S, vector<string> &L)
{
vector<int> rs;
if (L.empty()) return rs;
int len = L[0].length();
int num = 0;
int m = L.size()*len;
if (S.length() < m) return rs;
unordered_map<string, int> fixedTable;
unordered_map<string, int> countTable;
for (int i = 0; i < L.size(); i++)
{
fixedTable[L[i]]++;
}
for (int d = 0; d < len; d++)
{
for (int i = d; i <= S.length()-m; )
{
countTable.clear();
num = 0;//注意:清零,很严重的工作!!!
for (int j = i; j < S.length(); j+=len)
{
string t = S.substr(j, len);
if (!fixedTable.count(t))
{
i = j+len;
break;
}
if (countTable[t]<fixedTable[t])
{
countTable[t]++;
if (++num == L.size())
{
rs.push_back(i);
num--;
countTable[S.substr(i,len)]--;
i += len;
}
}
else
{
string t2 = S.substr(i, len);
for ( ; t2 != t; t2 = S.substr(i, len))
{
countTable[t2]--;
i += len;
num--;
}
i += len;
}
}
}
}
return rs;
}
};