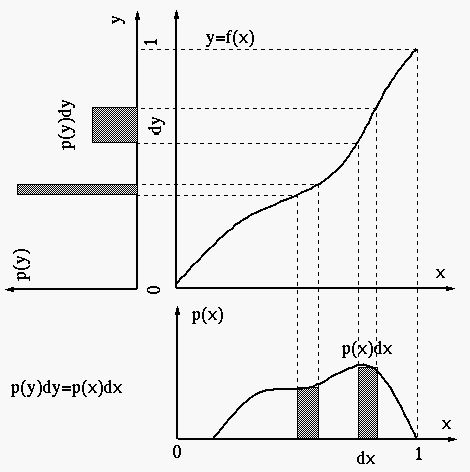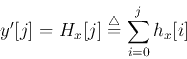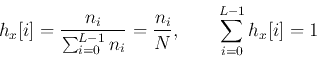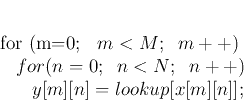直方图均衡化
直方图均衡化
直方图均衡化是对图像的灰阶进行变换,使变换后图像的直方图成为常量值:
目的:
l 均衡利用动态范围内的所有灰阶;
l 进一步做直方图规定(histogram specification)用.
我们首先假设范围内的灰度值是连续的,映射函数![]() 将x映射到同样取值范围内的y。我们再假设输入图像中
将x映射到同样取值范围内的y。我们再假设输入图像中![]() 区间内的灰度值被映射到输出图像的
区间内的灰度值被映射到输出图像的![]() 区间。由于映射前后的像素个数不变,所以有:
区间。由于映射前后的像素个数不变,所以有:
因为输出图像的直方图被均衡化了,其值应为1,即,所以有![]() ,于是可以得到:
,于是可以得到:
对两边求积分,我们就可以从直方图均衡化中获得映射函数:
直方图均衡化可以直观的理解如下:
l 如果![]() 值较大,那么
值较大,那么![]() 就会比较陡峭,
就会比较陡峭,![]() 就会比较宽,为了满足,会导致
就会比较宽,为了满足,会导致![]() 值比较小;
值比较小;
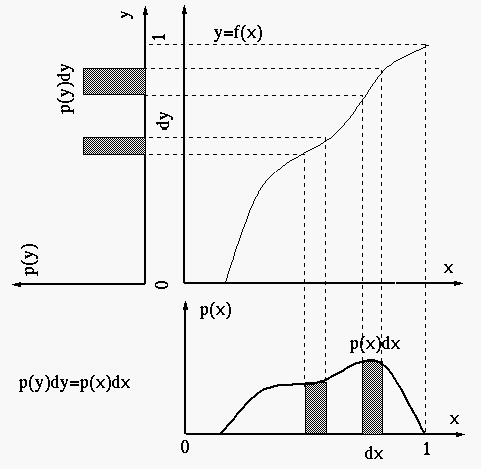
l 如果![]() 值较小,那么
值较小,那么![]() 就会比较平缓,
就会比较平缓,![]() 就会比较窄,会导致
就会比较窄,会导致![]() 值比较大。
值比较大。
当灰阶值为离散值时,输入灰阶x为范围内的一个离散值,此时连续的映射函数变为离散:
其中为灰阶值为i的像素个数,N为总像素个数。
1.
2.
其中![]() 是小于实数的最大整数值,加上0.5是为更准确地取整。注意,两种方法中都是将映射到最高灰阶值
是小于实数的最大整数值,加上0.5是为更准确地取整。注意,两种方法中都是将映射到最高灰阶值![]() ,而第二种变换中还
,而第二种变换中还![]() 将映射到0而使输出图像的灰阶值占据整个动态范围,第二种变换同时做了灰度值范围拉伸和直方图均衡。
将映射到0而使输出图像的灰阶值占据整个动态范围,第二种变换同时做了灰度值范围拉伸和直方图均衡。
例子:
假设图像大小为![]() ,灰阶个数为,下表显示了以上两种变换方法下的直方图均衡化过程:
,灰阶个数为,下表显示了以上两种变换方法下的直方图均衡化过程:
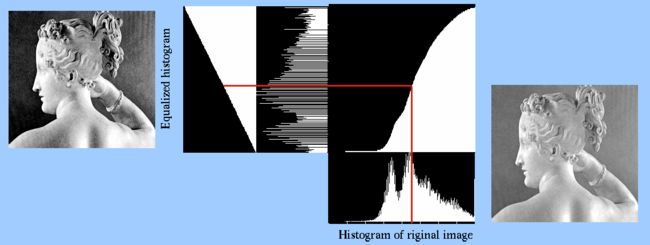
上面的例子表明给定图像的直方图被均衡化了。虽然均衡化的直方图看起来并不是一个常量值,但是其累计分布直方图是一条严格上升的斜线表明直方图确实被均衡化了。均衡化的直方图不能保证是一个常量值是由于同一个灰阶值的像素没有办法再被分开成多个灰阶的像素来保证达到均值分布。
编程问题:
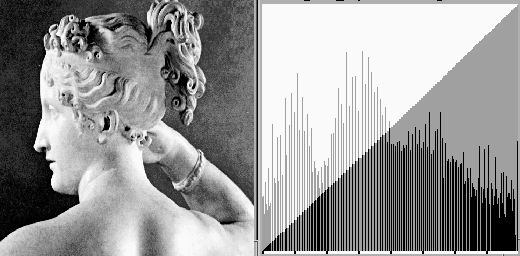
l 获取输入图像的直方图:
l 构建查找表:
l 图像映射:
例子:
原文:http://fourier.eng.hmc.edu/e161/lectures/contrast_transform/node2.html