hdu 2063(基础二分匹配)
对于无向图G=(V,E),如果V可以分为两个互不相交的子集(X,Y),并且图中的每条边所依附的两点属于不同的子集,则图G则称为一个二分图,所以二分图也可以记作G(X,E,Y)
边的描述:
e={x,y}
x来自G的顶点集X,y来自G的顶点集Y
我们说e连接顶点x和y,并说x和y与e关联
判断是否为二分图:
定理:一个无向图G=<V,E>是二分图当且仅当G中无奇数长度的回路。
匈牙利算法:
1.对于左边X的每个点,看看右边Y有没有增广路,如果有,那么进行增广,没有就不添加新的匹配。
2.当对最后一个点做完增广路以后,整个图就形成了一个最大匹配。
寻找交错路径(增广路)
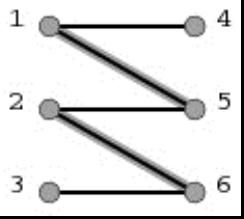
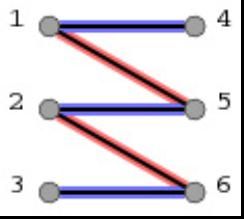
图1 图2
1)有奇数条边。
(2)起点在二分图的左半边,终点在右半边。
(3)路径上的点一定是一个在左半边,一个在右半边,交替出现。(其实二分图的性质就决定了这一点,因为二分图同一边的点之间没有边相连,不要忘记哦。)
(4)整条路径上没有重复的点。
(5)起点和终点都是目前还没有配对的点,而其它所有点都是已经配好对的。(如图1、图2所示,[1,5]和[2,6]在图1中是两对已经配好对的点;而起点3和终点4目前还没有与其它点配对。)
(6)路径上的所有第奇数条边都不在原匹配中,所有第偶数条边都出现在原匹配中。(如图1、图2所示,原有的匹配是[1,5]和[2,6],这两条配匹的边在图2给出的增广路径中分边是第2和第4条边。而增广路径的第1、3、5条边都没有出现在图1给出的匹配中。)
(7)最后,也是最重要的一条,把增广路径上的所有第奇数条边加入到原匹配中去,并把增广路径中的所有第偶数条边从原匹配中删除(这个操作称为增广路径的截断),则新的匹配数就比原匹配数增加了1个。(如图2所示,新的匹配就是所有蓝色的边,而所有红色的边则从原匹配中删除。则新的匹配数为3。)
hdu 2063代码:
#include<iostream>
#include<string.h>
using namespace std;
int pp[510][510];
int map[510] , vis[510];
int k,w,m;
int find_path(int x)
{
for(int i=1;i<=m;i++)
{
if(!vis[i] && pp[x][i])
{
vis[i]=1;
if(!map[i] || find_path(map[i]))
{
map[i]=x;
return 1;
}
}
}
return 0;
}
int main()
{
int a,b;
int sum;
while(scanf("%d",&k)!=EOF && k)
{
scanf("%d%d",&w,&m);
memset(pp,0,sizeof(pp));
memset(map,0,sizeof(map));
sum=0;
for(int i=0;i<k;i++)
{
scanf("%d%d",&a,&b);
pp[a][b]=1;
}
for(int i=1;i<=w;i++)
{
memset(vis,0,sizeof(vis));
if(find_path(i)) sum++;
}
printf("%d\n",sum);
}
return 0;
}