奇异值分解及应用(PCA&LSA)

这里我省去了很多的数学知识，建议数学比较薄弱的读者可以先看看<信息检索导论>第18章。主要的数学知识包括方阵的特征值、特征向量；方阵的对角化；一般矩阵的奇异值分解及低秩逼近矩阵。这里主要讲解奇异值分解的两个应用PCA(降维)和LSA(潜在语义结构分析)。

PCA:

之前有详细讲过PCA，见：http://blog.csdn.net/lu597203933/article/details/41544547。这里主要想讲解从SVD的角度去解决PCA.

PCA主要是为了寻找数据随之变化的主轴，我们都知道主轴的方向即为样本通过zscore归一化(即归一化后的均值为0，方差为1)的数据协方差矩阵所对应的最大特征值所对应的特征向量。而我们知道svd的定义如下公式：

A = UDV^T,这里假设A是m*n的矩阵，m是样本的数目，n为特征的数目。那么U为m*m的方阵且每一列都为A*A^T单位正交化的特征向量，V为n*n的方阵且每一列都为A^T*A单位正交化的特征向量，D为A*A^T(或A^T*A)的特征值的算术平方根构成的对角阵且为降序。

因此通过对数据进行归一化处理，A^T*A即为n维特征多对应的协方差矩阵，因此V的topK列就是我们需要寻找的PCA降维的前K个主轴.我们将其标注为[u1,u2,u3,…uk]其中ui都是向量。那么对于样本数据x⁽ⁱ⁾(n维)，[x^(i)T*u1, x^(i)T*u2,….x^(i)T*uk]即为降维后的数据(k维)。

LSA:

LSA(latent semanticanalysis,潜在语义分析),也可以写成LSI(latent semantic indexing,潜在语义索引)。它主要用来解决向量模型空间的一词多义(貌似解决不了)与一义多词问题。给出几个基础概念：

向量模型空间：向量空间模型是信息检索中最常用的检索方法，其检索过程是，将文档集D中的所有文档和查询都表示成以单词为特征的向量，特征值为每个单词的TF-IDF值，然后使用向量空间模型(亦即计算查询q的向量和每个文档di的向量之间的相似度)来衡量文档和查询之间的相似度(余弦距离)，从而得到和给定查询最相关的文档。

TF-IDF:词频（term frequency，TF）指的是某一个给定的词语在该文件中出现的频率。这个数字是对词数(term count)的归一化，以防止它偏向长的文件。（同一个词语在长文件里可能会比短文件有更高的词数，而不管该词语重要与否。）对于在某一特定文件里的词语来说，它的重要性可表示为：

其中n_i,j表示文档j中词i出现的次数

逆向文件频率（inverse document frequency，IDF）是一个词语普遍重要性的度量。某一特定词语的IDF，可以由总文件数目除以包含该词语之文件的数目，再将得到的商取对数得到：

   

其中

·    |D|：语料库中的文件总数

·    ：分母包含词语的文件数目（即的文件数目）如果该词语不在语料库中，就会导致分母为零，因此一般情况下使用作为分母。

然后再计算TF与IDF的乘积。

        

某一特定文件内的高词语频率，以及该词语在整个文件集合中的低文件频率，可以产生出高权重的TF-IDF。因此，TF-IDF倾向于过滤掉常见的词语，保留重要的词语。

布尔模型：

这也被称为布尔模型。

言归正传,千变万化的各种词的组合下隐藏着潜在语义结构空间(也被称为概念空间)，可以通过某种方式估计这中结构并去除噪音。

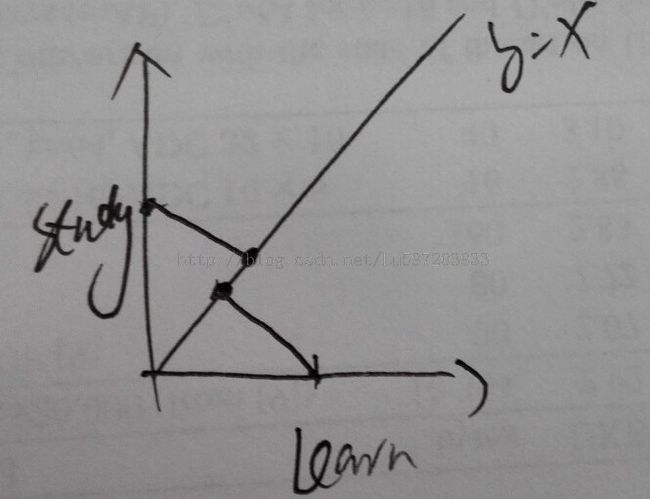
例如：两个样本x⁽¹⁾和x⁽²⁾,一个包含了study,一个包含了learn,那么用余弦计算它们的相似度，结果为0；但是我们将他们投影到某一方向向量上，如y=x的方向上，那么它们就变成正相关了，如下图。

目前，概念空间是通过奇异值分解的统计方法来估计的。具体为什么能通过奇异值分解进行估计我也没理解清楚，至少说没能像PCA那样从数学上推导出来，只能写一点算一点。(如果有更深入的理解，请评论指教，谢谢！)

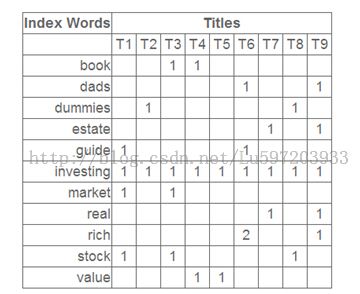
假定给我们的是一个词项-文档矩阵A，词项有100w个，而文档有50w个，这样原始矩阵就是100w*50w(词在文档中出现用1表示，不在用0表示)。那么此时我们对其进行奇异值分解，得到的就是U(100w*100w)，D(100w*50w), V(50w*50w)；奇异值最多可以有50w个。而LSA的思想就是我们一般保留上百个topK的奇异值(比如100个),那么我们用U_100w*100*D_100*100*V_100*50w的结果即为其潜在语义结构空间的表示，此时词项-文档矩阵仍然为100w*50w,它会将数据的语义信息考虑在内了，从而解决了一义多词的问题，这样我们就可以重新计算各个文档的相似性了。下面给出其算法具体步骤.

我们该如何去理解它呢，我们首要理解的是A*A^T,它的第i行第j列表示的是第i个词和第j个词项共同出现在文档的数目，而A^T*A的第i行第j表示的是第i个文档和第j个文档共同出现共同词的个数。而他们对应的特征向量U和V分别表示什么呢？

                                        

我们可以把这里的100看做是潜在的主题(或者概念),那么U的第i行第j列就可以看做是第i个词在第j个主题中的重要性，而V中的第i行第j列表示第i个主题在第j个文档中的重要性.而D中奇异值第i个奇异值就表示第i个主题的重要性。下面给出具体的数字。

                                   

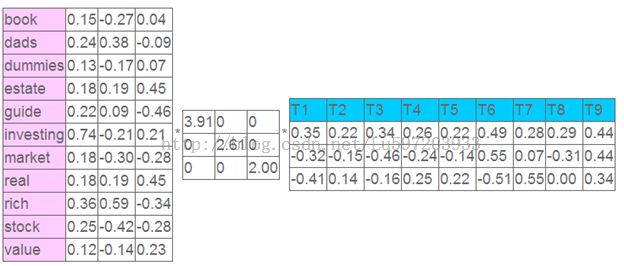
其对应的奇异值分解矩阵为(这里给出top3的奇异值)：

                                       

新的数据空间表示为：如计算A_new(1,1)

A_new(1,1) =0.15*3.19*0.35+(-0.27)*2.61*(-0.32)+0.04*2.0*(-0.41)表示的意思就是第i个主题在1个文档中重要性*第i个主题重要性*第1个词项在第i个主题中的重要性之和(i= 1,2..k)。这里摒弃了后面主题的重要性(如果保留所有的主题，就是原矩阵了)，就是一种去除噪音的做法，也就是无关信息（比如词的误用或不相关的词偶尔出现在一起），语义结构逐渐呈现；此外不为0奇异值的个数即为矩阵的秩，也可以看做是矩阵中线性无关向量的个数，而矩阵等同于坐标轴。原来矩阵的秩为9，那么现在矩阵的秩就是3，通过lsa就将数据有原来的9维空间变成了3维空间，相比传统向量空间，潜在语义空间的维度更小，语义关系更明确；类比于pca过程，降维是找到数据变化的主轴，就可以将文档在高维向量空间模型中的表示投影到低维的潜在语义空间中了。

参考文献：

1：书籍：信息检索导论

2: http://blog.csdn.net/abcjennifer/article/details/8131087数学之美

3：http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用

4：http://www.cnblogs.com/kemaswill/archive/2013/04/17/3022100.html

5：http://read.pudn.com/downloads126/sourcecode/graph/texture_mapping/536657/pLSA/pLSA.pdf