dancing links详解
Dancing links是一种能高效实现Knuth的X算法的技术,它可以使很多搜索问题得到极大的优化。
假设x是一个双向链表中的一个节点,L[x]表示X的前驱,R[x]表示x的后继,
则R[L[x]] = R[x], L[R[x]] = L[x]这一操作可以把x从链表中移除,这是众所周知的,
当然,一个细致的程序员还会用 L[x] = R[x] = x或 L[x] = R[x] = NULL这样的操作来清除x,
以免发生内存泄露,所以只有很少的程序员意识到,若不清除x则 R[L[x]] = x, L[R[x]] = x
这个操作可以把刚才移除的x恢复到之前的链表中,而这样的恢复功能在有些时候是很有用的,
例如,在一个交互性的程序中,用户很可能想撤销他所做的一个或一系列操作,恢复到先前的状态。
另一个典型的应用是在回溯程序中。
精确覆盖问题:给出一个集合S={a,b,c,d,e,f,g}的一些子集S1={c,e,f}, S2={a,d,g},
S3={b,c,f}, S4={a,d},S5={b,g}, S6={d,e,g},选取哪些子集可以使得A中的元素全部出现并只出现一次,
即用那些子集可以完全覆盖全集S,并且保证没有元素会被重复覆盖?
({S1={c,e,f},S4={a,d},S5={b,g}}是一组解)
我们可以用一个0-1矩阵来表示这些集合:
矩阵M中每一列对应全集中的一个元素,若M[row=i][col=j]=1则表示集合i包含j元素,
如:第一行S1的c、e、f列为1表示S1包含元素c、e、f。
因此我们可以把之前的问题描述为:给定一个由0和1组成的矩阵M,是否能找到一个行的集合,
使得集合中每一列都恰好包含一个1?
不管怎么说,这都是一个很难的问题,当每行恰包含3个1 时,这是个一个NP-完全问题,自然,
作为首选的算法就是回溯了。
解决精确覆盖问题: Knuth 的X算法,它能够找到由特定的01矩阵定义的精确覆盖问题的所有解。
X算法:
上面的算法可能看起来有点晕,其实它是一个典型的递归深搜算法,它所表达的含义和思想是这样的:
例如矩阵M,它其实描述了S1={c,e,f}, S2={a,d,g}, S3={b,c,f}, S4={a,d}, S5={b,g}, S6={d,e,g}这些集合,
如果我们要用这些集合去覆盖集合S={a,b,c,d,e,f},我们可以先选择一个集合使得S中的第一个元素:
a(也就是矩阵中的第一列)被覆盖掉,在矩阵中我们从上往下找,发现S2包含元素a(在矩阵中M[row=S2][col=a]为1),
假如我们选择S2,则a、d、g列都将会被覆盖,后面我们只需把b、c、e、f列覆盖掉就行了,
所以,我们把矩阵的a、d、g三列全部覆盖掉,又由于问题中还有一个限制条件,
即一个元素不能被重复覆盖,所以当我们选择了S2={a,d,g}后, S4={a,d}、S5={b,g}、S6={d,e,g}将不能被选,
它们都与S2有交集,所以我们把S4、S5、S6同S2一起覆盖掉,于是我们得到了一个比M小的矩阵M’。
我们剩下的问题就是用剩下的集合S1、S3去覆盖集合S’={b,c,e,f}。

我们剩下的工作便是再次使用x算法把M’矩阵精确覆盖即可,当然,
从图中我们发现S1={c,e,f}和S3={b,c,f}并不能精确覆盖S’={b,c,e,f},
所以我们之前选择S2是个错误的选择,于是我们需要往前回溯,不选择S2,
从S2行往下找,发现S4的第a列为1,于是我们选择S4,然后继续以上的操作
直到把矩阵完全覆盖。
选择S4覆盖后得到的矩阵M’’:
X算法的实现:通过观察上面的列子可知,随着递归的深入,需要搜索的矩阵的规模将会变得越来越小,
有些读者也许会很容易想到链表。因为链表可以高效的支持删除操作,并且其长度也将随着删除操作的执行而变短。
但是X算法不仅要删除操作,在回溯的过程中还需要恢复操作,aha!前文所提到的内容派上用场了,
我们可以用如下图所示的双向十字链表(我们把这种结构叫做dancing links)高效实现X算法。

Dancing links的具体实现:通常有两种方法可以实现dancing links,一种是用指针实现,
这种方法比较好理解,但编码麻烦一些,一种是用数组实现,这种方法不如用指针直观,
但更容易编码。
数组方法实现dancing links:用数组L[N]储存0到N-1号节点的左边节点的下标,
用数组R[N]储存0到N-1号节点的右边结点的下标,同理,U[N]、D[N]两个数组表示上下两个方向的信息。
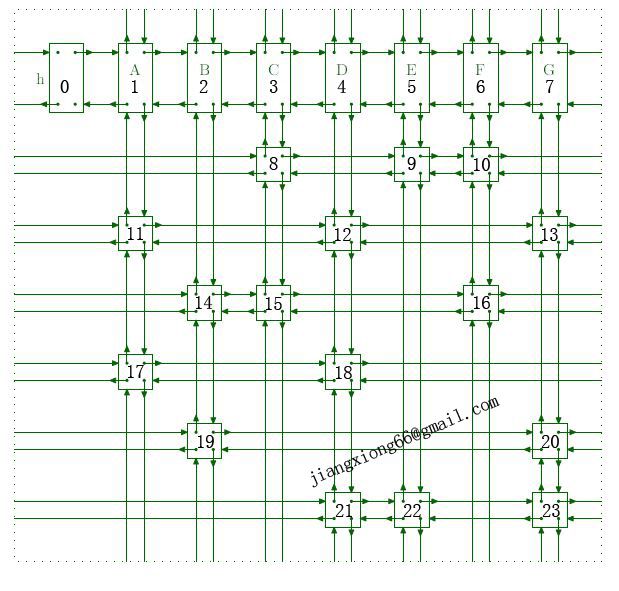
上图中的数字表示节点的下标,我们把头节点head编号为0,列分别编号为1,2,3,4,5,6,7。
上图的dancinglinks结构可用如下4个数组描述。
明确了数据结构,剩下的编码便容易了。
#define head 100
int U[N],D[N],L[N],R[N];
int C[N],H[N],ans[N];//C[N]表示N的列标,H[N]表示N的行标,ans[]用来储存结果
bool dance(int k)
{
int c = R[head];
if(c==head) {
Output();//Output the solution
return true;
}
remove(c);
for(int i=D[c]; i!=c; i=D[i])
{
ans[k] = H[i];
for(int j=R[i]; j!=i; j=R[j]) remove(C[j]);
if(dance(k+1)) return true;
for(int j=L[i]; j!=i; j=L[j]) resume(C[j]);
}
resume(c);
return false;
}
void remove(int c)
{
L[R[c]] = L[c];
R[L[c]] = R[c];
for(int i=D[c]; i!=c; i=D[i]) {
for(int j=R[i]; j!=i; j=R[j]) {
U[D[j]] = U[j];
D[U[j]] = D[j];
}
}
}
void resume(int c)
{
L[R[c]] = c;
R[L[c]] = c;
for(int i=U[c]; i!=c; i=U[i]) {
for(int j=R[i]; j!=i; j=R[j]) {
U[D[j]] = j;
D[U[j]] = j;
}
}
}
函数remove(c)可将c列删除,并将c列上为1的行从矩阵中删除。
函数resume(c)的作用和remove(c)相反,它可将c列恢复到矩阵,并将c列上为1的行也恢复到矩阵中。
执行remove(c=1)后,R[head] = 2, L[2] = head, D[4] = 21,U[21] = 4, D[7] = 20, U[20] = 7,
其他的信息则没有发生改变,remove(c=1)的效果如下图所示



