Deep Learning(深度学习) 学习笔记(二)
前言:昨天看到微博上分享的深度学习视频,为上海复旦大学吴立德教授深度学习课程,一共六课时,视频地址点击打开链接。在此我结合其他资料,写点个人的学习笔记进行记录。
第二课:前馈神经网BP算法
本课吴老师对深度学习前馈神经网BP算法做介绍。内容分为两块:1.前馈网基本概念 2.BP算法
1前馈网基本概念
1.1.基本概念:
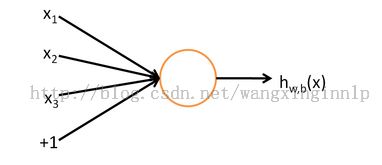
神经元
图1,神经元 (图片来自http://deeplearning.stanford.edu/wiki/index.php/%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C)
神经元输入: ![]()
神经元输出: ![]()
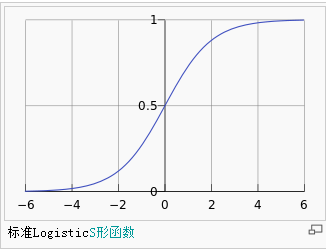
**神经元就是神经网络的基本运算单元。![]() 中的函数叫做激活函数 (activation function)。激活函数一般有两种选择:sigmoid函数或者tanh函数
中的函数叫做激活函数 (activation function)。激活函数一般有两种选择:sigmoid函数或者tanh函数![]() 。两者的不同之处是前者的输出范围是(0,1)(见图2)后者的输出范围是(-1, 1)(见图3)。
。两者的不同之处是前者的输出范围是(0,1)(见图2)后者的输出范围是(-1, 1)(见图3)。
神经元就是一个![]() 和
和![]() 套在一起的复合函数组成,其中外层是一个非线性函数和内层是一个线性函数,组成的是一个多元函数。展开写就是
套在一起的复合函数组成,其中外层是一个非线性函数和内层是一个线性函数,组成的是一个多元函数。展开写就是![]() 。
。
图3.tanh函数(图片来自http://deeplearning.stanford.edu/wiki/index.php/%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C)
神经层
图4.神经层
**多个神经元可以组成一个神经层。如图4,图4中的神经层由3个神经元组成。这3个神经元的输入x是相同的,但是他们各自神经元上的权重w(也就是图4中带箭头的线上的权重)向量是不同的。现在神经层的输出不是一个简 单的数了,是一个向量y。一层神经层可以看做是输入向量x映射成为输出向量y。
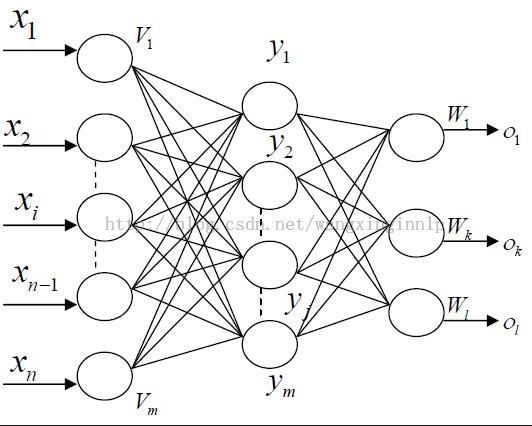
神经网
图3.神经网络,图片来自web
**如果我们将多个神经层叠起来,我们可以得到神经网。每次层的输入(如果有的话)是上一层的输出。
2.基本符号
![]() 神经网络的层数。
神经网络的层数。
第![]() 层神经元的个数
层神经元的个数
第![]() 层神经元激活函数
层神经元激活函数
上述参数均是超参数:这些参数是人为的根据具体的问题定义的,这些参数就决定了所使用神经网络的基本结构。
![]() 第l层到第l+1层的连接权重(就是图4中带箭头线上的权重)
第l层到第l+1层的连接权重(就是图4中带箭头线上的权重)
![]() 第l层到第l+1层的偏置(一般画图中每一层最下面的节点就似乎偏置节点)
第l层到第l+1层的偏置(一般画图中每一层最下面的节点就似乎偏置节点)
可训练参数:我们算法需要去训练优化的参数
![]() 第l层神经元的状态
第l层神经元的状态
![]() 第l层神经元的激活值
第l层神经元的激活值
1.3,前馈计算
1.3.1 基本关系
第l+1层的状态是由前面第l层的激活值线性计算所决定。
![]() 第l+1层的激活值由第l+1层的状态通过激活函数决定。
第l+1层的激活值由第l+1层的状态通过激活函数决定。
由上述公式不难得出:![]() 这就是第l+1层状态和第l层状态的关系。
这就是第l+1层状态和第l层状态的关系。
1.3.2 前馈计算
如果已经知道每一层的w和b值(也就是给定神经网络模型)。由第一层,我们可以计算出第2层的状态,然后通过第二层的激活函数算出第二层的激活值a2, 继续我们计算第三层的状态值和激活值,直至最后一层。
![]()
这样我们就由输入x经过神经网络计算后得到我们的输出。
1.4.用于ML
数据:![]()
模型:![]()
准则: 准则左边是对所有的样本的代价函数加和。准则右边是规则化项,防止过拟合。
我们的优化目标就是:
优化目标可以写成
对于这个目标,可以使用梯度下降法求解。
使用梯度下降法的关键部分就是求其偏导数:
**注意1,针对我们的准则中cost function J。我们虽然有四个参数![]() ,但是给定样本后,前两个参数已经固定。能变的只是后两个参数w和b。
,但是给定样本后,前两个参数已经固定。能变的只是后两个参数w和b。
2,此处写法中的w和b都是变量向量,而不只是一个变量。
如果有了其偏导数,我们给定迭代步长,就能够慢慢的去寻找目标函数最小值。但是由于我们的目标函数是非凸的,找到的可能只是局部最优。
BP算法就是一种计算偏导数的算法。
2. BP算法:
关于BP算法,我觉得这几篇博客可以进行参考:
1.点击打开链接 [此博客讲的非常赞]
2.点击打开链接
3.点击打开链接
在用到如果你了解线性回归和逻辑斯底回归,他们调节参数也是使用梯度下降法,但是他们却在求偏导数的没有神经网络这么复杂。这是为什么呢?神经网络求偏导数有什么与众不同之处?
参考上述3篇文章需要了解两个问题:1,为什么每次跟新权重需要单个样本(每个样本来一遍)来跟新(感知机也是)。把所有样本的残差累加起来一起跟新行不行? (貌似是可以的,随机梯度和批量梯度的区别。)2, 为什么隐层的跟新需要其残差,直接使用损失函数对其权重变量求偏导行不行?(避免重复计算。)
注意:到目前为止,将的都还是神经网络,还没涉及深度学习。
在神经网络中,两个经常遇见的名称“对称失效”(symmetry breaking)“梯度弥散”(gradient diffusion)。在此做个解释(我自己的理解):
1,对称失效
我们在使用BP算法进行梯度下降的时候,优化目标是非凸的。也就是说我们是使用不同的初始值初始化我们那些参数(所有的 权重w 和 偏置b)可能得到局部最优值。如何选取初始值是一个令人头痛的问题。一般都是采用随机初始化。但是不能让所有参数都用相同的值作为初始值,这样会出现问题。
假设现在我们使用所有相同的值q初始化参数,在我们神经网络中每一层中所有的神经元状态都相等,激活值都相等。在进行BP算法进行梯度计算的时候。我们的每一层神经网络神经元的梯度也会相同。下面来看看为什么。我们的梯度是根据残差来计算的(BP算法参考点击打开链接)。
第![]() 层残差 和 第 层残差关系:
层残差 和 第 层残差关系:
**每一层的残差现在相等了
第![]() 层梯度和第层残差的关系:
层梯度和第层残差的关系:
**每一层的残差相等,在计算第L层时候,第L+1层残差相等,并且由于我们的初始化策略导致每一层神经元的权重和激活值是相等的,不难看出每一层中单个神经元的梯度是相等的。这样有趣的事情发生了,同一层神经元,不管你如何迭代,他们的权重始终保持相等(这应该就是所谓的对称吧)。我们随机化初始目的就是不让这种对称性出现,也就是对称失效。
2,梯度弥散(也称 梯度扩散)
貌似有的博客在说采用BP算法在训练神经网络时候会出现梯度弥散问题,也就是说残差传播到最前面一层的时候变得很小,几乎无法进行有效调参。 这让我很迷惑,让我觉得是BP算法才有梯度弥散问题。但是根据下面公式我迟迟得不到想要的结论:
如果我们激活函数采用sigmoid函数,最右边是小于等于0.25。但是左边有一个W,无法判断是否有影响。后来我查到一篇论文《Discriminative Learning of Sum-Product Networks》,其指出:Standard gradient descent suffers from the diffusion problem(标准的梯度下降法经常遇到梯度扩展问题)。眼前豁然开朗。
从梯度下降考虑就可以使问题明了。简单举例(以下都是z自变量x z和因变量y均为标量,非向量):
![]()
y分别z 和 x求导数及其关系:
现在我们f2函数假设为sigmiod函数,其导数小于0.25[上面已经解释], 我们就会发现问题。在我们这个简单的函数中外层导数(对z)和内层导数(对x)就差了大一截。如果我们继续套几个函数,那么到比较内层的导数就会变得很小很小。继续推广一下到多层多个变量的情况,就是最前面几层的梯度会很小,在更新梯度的时候无法产生影响。梯度本来就小,在梯度更新时候还得乘上一个很小的迭代步长(迭代步长不能设置大,不然会在极值附近一直绕),结果是那个变量的值就会产生很小很小的更新,几乎是无法更新。这就是所谓的梯度扩散。