静态Instruction-Cache锁定策略--RTAS09论文(优化问题)
今天读了一篇RTAS09(嵌入式方面国际顶级会议)年的论文,很有启发,在此记录下来。
---------------------------------------------------------------------------------------------------------------------
论文:Minimizing WCET for Real-Time Embedded Systems via Static Instruction Cache Locking
---------------------------------------------------------------------------------------------------------------------
首先该论文解决的问题是降低一个程序执行的最坏执行时间(WCET, worst case execution time),因为这对于嵌入式系统(实时)有很重要的影响。指令Cache能够提升读取指令的平均访问时间,但在一定程度上,因为读取Cache的命中不确定性,使得程序执行时间反而更加不可预测。所以有时候甚至会选择不使用指令Cache来提高对执行时间的可预测性(实时系统必须保证程序能在所要求时间里面执行完成)。不过现在很多CPU都提供了对于指令Cache的锁定功能,即可以让某段代码一直存在于Cache里面不会被替换出去。
然而I-Cache的大小总是有限的,那么怎么选择程序中的哪些代码(或者函数)被锁在指令Cache里面,来使得WCET最小(问题1)。
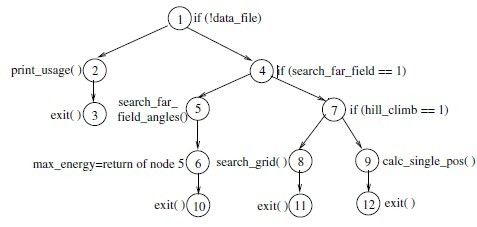
论文对程序的执行建立了一个EFT(execution flow tree)模型,看一个例子就知道EFT表示什么意思:
if (!data_file) { print_usage(); exit(1); } if (search_far_field == 1) { 4 if (search_far_field == 1) search_far_ exit( ) 3 field_angles() print_usage( ) 2 1 if (!data_file) max_energy = search_far_field_angles(max_result, data_file, output_file, hamming); } else if (hill_climb == 1) { search_grid(source_location, data_file, output_file, hamming); } else { calc_single_pos(source_location, mic_locations, hamming, data_file, output_file); } exit(0);
这段代码对应的EFT:
当然,对于节点2、5、8、9没有递归地展开。
注:我这里对EFT就简单通过这个例子说明,具体的定义等可以参考论文
这样我们可以在编译的时候通过一个算法(可以构造)得到程序的执行EFT(V,E),V是节点集,E是边集。
着重要说明的是V表示的是具体的执行路径上的节点,并非是真正的实体代码。什么意思呢,就是说不同的节点i和节点j,他们可能是同一个函数的执行节点,这完全有可能,不同路径调用同一个函数(我们给的例子没有出现这种情况)。
因此我们有必要在定义一个函数(代码)集F来表示正真的代码节点
对于节点i属于V,我们可以定义一些u的属性:
W(i) 表示函数(代码)i如果在内存中的执行时间
W'(i) 表示函数i如果在I-Cache中的执行时间
name(i) 表示执行节点i对应的函数(代码)节点,f=name(i)
s(f) 表示函数f所占的字节大小
由此:我们可以将问题1抽象为下面问题2
给定一个大小为S的I-Cache,一个EFT(V,E)图与函数集F,将大小不超过S的函数集X(X包含于F)放入I-Cache,使得EFT(V,E)中最长执行路径最短。(问题2)
P是所有执行路径集合,num(Pi)是路径i的长度,约束条件s.t.第一条其实就是L取所有执行路径长度的最大值。执行路径Pi上每个节点j要么取W(Pij),要么取W'(Pij),看&(f)(那个符号打不出)的取值(即f是否在I-Cache中),就是 (1-&(f))*W(pij) + &(f)*W'(pij)。
得到一个整数规划问题,论文中证明这是一个NP-Hard问题。因此有些研究者使用了一些贪心算法或者遗传算法来计算近似解。
这篇论文对该问题添加了一些限制条件,在一定条件能在多项式时间里求解出最优解。
限制:每个函数不会出现在不同的执行节点中,即节点i和节点j,如果i!=j,那么name(i)!=name(j)
这表明函数不会reuse。也就是说如果选择节点i进入I-Cache,那么不会存在另外一个节点j,使得它的执行时间也从W(j)变成W'(j)。
我们将多叉树EFT(V,E)转化为与其等价的二叉树BEFT(V,E') (标准算法,第一个孩子是左孩子,后面第一个兄弟是右孩子)
该问题可以用动态规划来解决。首先我们定义子问题:
OPT[v][i]表示以v为根的那棵子树,当有大小为i的I-Cache可以使用时,所达到的最小WCET。这样就有 |V|*|S+1|个子问题(S+1包含了i=0的情况)。
当前已经得到节点v的孩子的OPT,那么如果转移求解子问题OPT[v][i]:
1.如果v不包含进I-Cache
那么可以将大小为i的Cache分给两个孩子为根的子树,枚举左孩子子树使用Cache大小为j,那么右子树可以使用i-j大小的Cache。注意右子树在EFT中是v的右边第一个兄弟,所以不需要加W(v),因为和v不在同一执行路径中。故要使得两条路径中最大值最小。
2.如果v包含进I-Cache
那么v使用掉大小为s(v)的Cache,枚举给左孩子的Cache大小j,那么右孩子可以使用i-s(v)-j大小的Cache。
在1和2中取小的组成OPT[v][i],得
DP转移方程:
其中a(v)=0表示v不包含进I-Cache,a(v)=1表示v包含进I-Cache。在O(|V|*|S|*|S|)复杂内得解。
这里求出的OPT(v,i)是BEFT中以v为根的子树的优解,在EFT中该OPT(v,i)表示所有以v为根或者以v的右边所有兄弟为根的子树的最优解中的最大值。
一些启示:
1.RTAS是顶级会议,可见这篇论文的质量,虽然我没有把这篇论文所有贡献都写出来,但是也列出了些核心内容。说明顶级会议并不是那么遥不可及(^_^)。
2.这篇论文与其说讨论体系结构方面或者嵌入式方面,不如说是一篇纯讨论算法的论文,建立模型,然后对模型的分析和求解。今后也可以考虑在体系结构研究中使用抽象建模的方式来量化分析或者最优化分析一些问题。