poj1113

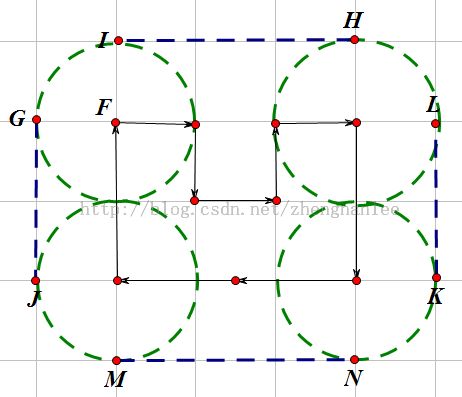
标准的凸包题目，题目不难理解，就是求走一周的路程。

结果等于，凸包周长+一个完整的圆周长。

因为走一圈，经过拐点时，所形成的扇形的内角和是360度，故一个完整的圆。

坑得的精度，四舍五入！=（int）类型强制转换。。。

#include <iostream>
#include <math.h>
#include <algorithm>
#include <stdlib.h>

using namespace std;

#define pi acos(-1.0)
#define eps 1e-8
#define zero(x) (((x)>0?(x):-(x))<eps)

struct point{ double x, y; }p[1005], convex[1005];

double dis(point a, point b)
{
	return sqrt((a.x - b.x)*(a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}

//计算cross product (P1-P0)x(P2-P0)
double xmult(point p1, point p2, point p0){
	return (p1.x - p0.x)*(p2.y - p0.y) - (p2.x - p0.x)*(p1.y - p0.y);
}
//graham算法顺时针构造包含所有共线点的凸包,O(nlogn)
point p1, p2;
int graham_cp(const void* a, const void* b){
	double ret = xmult(*((point*) a), *((point*) b), p1);
	return zero(ret) ? (xmult(*((point*) a), *((point*) b), p2) > 0 ? 1 : -1) : (ret > 0 ? 1 : -1);
}
void _graham(int n, point* p, int& s, point* ch){
	int i, k = 0;
	for (p1 = p2 = p[0], i = 1; i<n; p2.x += p[i].x, p2.y += p[i].y, i++)
		if (p1.y - p[i].y>eps || (zero(p1.y - p[i].y) && p1.x > p[i].x))
			p1 = p[k = i];
	p2.x /= n, p2.y /= n;
	p[k] = p[0], p[0] = p1;
	qsort(p + 1, n - 1, sizeof(point), graham_cp);
	for (ch[0] = p[0], ch[1] = p[1], ch[2] = p[2], s = i = 3; i < n; ch[s++] = p[i++])
		for (; s>2 && xmult(ch[s - 2], p[i], ch[s - 1]) < -eps; s--);
}

int wipesame_cp(const void *a, const void *b)
{
	if ((*(point *) a).y < (*(point *) b).y - eps) return -1;
	else if ((*(point *) a).y > (*(point *) b).y + eps) return 1;
	else if ((*(point *) a).x < (*(point *) b).x - eps) return -1;
	else if ((*(point *) a).x > (*(point *) b).x + eps) return 1;
	else return 0;
}

int _wipesame(point * p, int n)
{
	int i, k;
	qsort(p, n, sizeof(point), wipesame_cp);
	for (k = i = 1; i < n; i++)
		if (wipesame_cp(p + i, p + i - 1) != 0) p[k++] = p[i];
	return k;
}

//构造凸包接口函数,传入原始点集大小n,点集p(p原有顺序被打乱!)
//返回凸包大小,凸包的点在convex中
//参数maxsize为1包含共线点,为0不包含共线点,缺省为1
//参数dir为1顺时针构造,为0逆时针构造,缺省为1
//在输入仅有若干共线点时算法不稳定,可能有此类情况请另行处理!
int graham(int n, point* p, point* convex, int maxsize = 1, int dir = 1){
	point* temp = new point[n];
	int s, i;
	n = _wipesame(p, n);
	_graham(n, p, s, temp);
	for (convex[0] = temp[0], n = 1, i = (dir ? 1 : (s - 1)); dir ? (i < s) : i; i += (dir ? 1 : -1))
		if (maxsize || !zero(xmult(temp[i - 1], temp[i], temp[(i + 1)%s])))
			convex[n++] = temp[i];
	delete []temp;
	return n;
}

int main()
{
	int n;
	double d;
	while (cin >> n >> d)
	{
		memset(p, 0, sizeof(p));
		memset(convex, 0, sizeof(convex));
		double dist = 0.0;
		for (int i = 0; i < n; i++)
		{
			cin >> p[i].x >> p[i].y;
		}
		//cout << n << endl;
		int size = graham(n, p, convex,0);
		//cout << size << endl;
		for (int i = 0; i < size - 1; i++)
		{
			dist += dis(convex[i], convex[i + 1]);
		}
		dist += dis(convex[size - 1], convex[0]);//别忘了起始到结束的长度
		cout << (int) (dist + 2 * pi * d + 0.5) << endl;
	}
}

额这代码多亏川姐提醒，，四舍五入- -。。。。。。