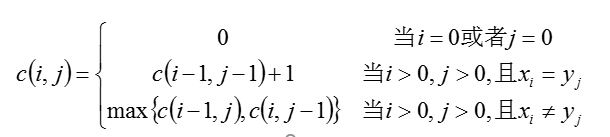LCS算法的C++实现

这两天忙里偷闲看了July的团队提供的LCS算法视频，真的如视频标题一样，十分钟搞定LCS算法。

感谢July大神，感谢其团队的邹博。

这里附上视频链接：http://www.julyedu.com/video/play?course=17

说是十分钟搞定，其实是不包括程序实现部分。视频中队程序部分没有做讲解，而且PPT中提供的原码貌似是 Pascal 的？

因此我自己用C++做了其算法的实现，关于算法的分析就看视频吧，讲解真的很详细。

目标一：

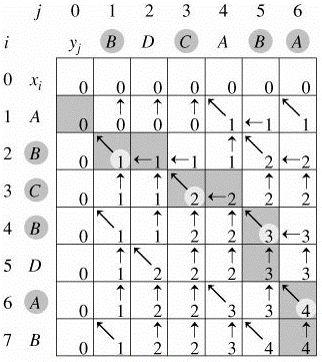
实现下图中的矩阵

首先根据要比较的x,y字符串构造二维数组c，维度是x和y的长度+1，用于记录最长公共子序列长度

xlen=x.length();
ylen=y.length();
int c[xlen+1][ylen+1];

接着是n数组，记录方向，我用0代表左，1代表上，2代表左上

int n[xlen][ylen];//0-left 1-top 2-left-top

对于c数组，将第0行和第0列赋值为0

for(i=0;i<=xlen;i++)
	 c[i][0]=0;
for(j=0;j<=ylen;j++)
	 c[0][j]=0;

然后是一个二重循环，给数组c和n赋值

c数组依据的公式是

n[i,j]取值的依据是

如果x(i-1)=y(j-1)，那么n[i,j]=2;

如果x(i-1)!=y(j-1),且c[i-1,j]>=c[i,j-1]，那么n[i,j]=1;

如果x(i-1)!=y(j-1),且c[i-1,j]<c[i,j-1]，那么n[i,j]=0;

因此：

for(i=1;i<=xlen;i++)
    {
       for(j=1;j<=ylen;j++)
       {
            if(x.at(i-1)==y.at(j-1))
            {
                 c[i][j]=c[i-1][j-1]+1;
                 n[i-1][j-1]=2;
            }
            else
            {
                c[i][j]=c[i-1][j]>c[i][j-1]?c[i-1][j]:c[i][j-1];
                n[i-1][j-1]=c[i-1][j]>=c[i][j-1]?1:0;
            }
       }
    }

到此已经完成了对c,n数组的赋值。n的最后一个数就存储着最长公共子序列的长度

根据n的方向指示，就可以找出最长公共子序列

i=xlen-1;
   j=ylen-1;
   while(1)
   {
       if(i==0||j==0)
       {
          if(n[i][j]==2)
            s+=x.at(i);
          break;
       }
        if(n[i][j]==0)
        {
            j--;
        }
        else if(n[i][j]==1)
        {
           i--;
        }
        else
        {
            s+=x.at(i);
            i--;
            j--;
        }
   }

邹博的PPT中给的寻找最长公共子序列的实现用的递归。但是我尝试用单独的函数实现的时候，发现在用二维数组作为函数参数上遇到了问题，暂时没找到更好的办法，因此就干脆弃用递归，用while循环实现。（毕竟都说递归效率不高，只能这样安慰自己了23333）

上面的while循环给出的字符串s并不是最长公共子序列，而是其反序的结果，因此将其反向输出就是我们要的结果了

 for(i=s.length()-1;i>=0;i--)
     cout<<s.at(i)<<" ";

源程序GitHub地址： https://github.com/hebecherish/lcs/