OpenMP: 循环结构的并行
在科学和工程应用中,许多程序都要在循环执行上花大量的时间,如Fortran中的do循环和C语言中的for循环,通过并行中的loop-level可以减少这些循环的运行时间。OpenMP提供了parallel for或parallel do指令来对循环结构进行并行处理,这个指令可以用于大部分的循环结构,它也是OpenMP中使用最多和最频繁的指令。当然,程序员必须清楚哪些循环是可以进行并行的。
OpenMP中用于循环的指令结构为:
#pragma ompparallel for [clause [clause …]]
for循环结构
注:方括号[]表示可选项。
在parallel for或parallel do指令后,紧接着就必须是for循环(对于C语言)或do循环(对于Fortran语言),并形体就是for或do循环中的程序。只是在fortran中还可以添加!$omp end parallel do指令来表示循环并行结束。OpenMP还提供了用于控制并行执行的一些循环选项条件(clause),根据这些条件的类型可以分为范围条件、schedule条件、if条件、ordered条件和copyin条件等。
范围条件
范围条件主要有default(shared | none)、shared(list)、private(list)、firstprivate(list)、lastprivate(list)和reduction(operator:list)等。default条件用于设置并形体中涉及到的变量默认是shared共享的还是非共享的,default后的括号中只有值shared或none。shared条件表示其后list列出的那些变量在并形体中是共享的,意思就是说并形体外部和并形体内部都可以对该变量进行读取和修改,它就像全局变量一样。
private条件用于表示其后list列出的那些变量在并形体中是私有的。既然是私有的,那么在并形体外部设置的该变量值无论为多少,在并形体中都将无法使用。所有这些private变量在并形体中都必须初始化设置值,换句话说,这些private的变量在并形体中与在并形体外是完全隔离的、毫无关系的。在for循环中定义的循环变量默认就是private的。下面举一个例子来说明private,如下代码:
// File: PrivateTest.cpp : 定义控制台应用程序的入口点。
#include<omp.h>
#include<iostream>
using namespace std;
//private测试
int PrivateTest()
{
cout<<"private输出:\n";
inti=0,j=10;
#pragmaomp parallel for private(j)
for(i=0;i<8;i++)
{
cout<<i<<":"<<j<<"\n";
j++;
cout<<i<<":"<<j<<"\n";
}
return0;
}
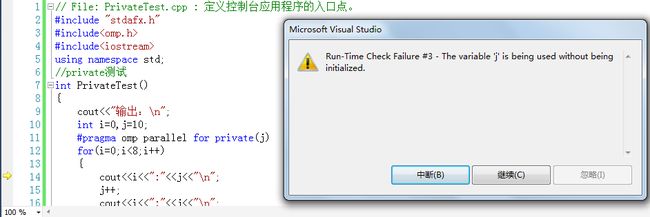
如果运行该程序,将会出现变量j没有初始化的错误,错误提示如下图所示:
奇怪的是为什么没有提示i?因为i已经初始化为0,而并形体中还没有为j设置初始化值,如果将j=10添加到for循环中,程序就运行正常了。如下代码(红色表示修改的部位):
// File: PrivateTest.cpp : 定义控制台应用程序的入口点。
#include<omp.h>
#include<iostream>
using namespace std;
//private测试
int PrivateTest()
{
cout<<"private输出:\n";
int i=0,j=10;
#pragmaomp parallel for private(j)
for(i=0;i<8;i++)
{
j=10;
cout<<i<<":"<<j<<"\n";
j++;
cout<<i<<":"<<j<<"\n";
}
return0;
}
firstprivate条件用于表示其后list列出的变量在并形体中私有的,但其在并形体中的初始化值为并行之前设置的值。同样以上面的代码为例:
// File: FirstPrivateTest.cpp : 定义控制台应用程序的入口点。
#include<omp.h>
#include<iostream>
using namespace std;
//FirstPrivateTest测试
int FirstPrivateTest()
{
cout<<"firstprivate输出:\n";
inti=0,j=10;
#pragmaomp parallel for firstprivate(j)
for(i=0;i<8;i++)
{
cout<<i<<":"<<j<<"\n";
j++;
cout<<i<<":"<<j<<"\n";
}
return0;
}
该代码与之前代码没有什么太大区别,尽管在并形体中没有对j进行初始化,但是它能正常正确的运行,其原因就是将变量j设置成了firstprivate。虽说在并形体中并没有对j进行初始化,但是在并形体中j的初始值就是10。
lastprivate条件与firstprivate的含义类似,只是它设置的变量需要在并形体中初始化,但是其最后的结果可以在并形体外部使用。
// File: LastPrivateTest.cpp : 定义控制台应用程序的入口点。
#include<omp.h>
#include<iostream>
using namespace std;
//LastPrivateTest测试
int LastPrivateTest()
{
cout<<"lastprivate输出:\n";
inti=0,j=10;
#pragmaomp parallel for lastprivate(j)
for(i=0;i<8;i++)
{
j=5;
cout<<i<<":"<<j<<"\n";
j++;
cout<<i<<":"<<j<<"\n";
}
cout<<"最后j的值为:"<<j<<"\n";
return0;
}
最后输出的j的值为6,注意,j的值不是10,也不是11,也不是5+8=13,而是5+1=6。另外,如果设置变量为lastprivate,它必须在并形体中初始化,否则会出错。
reduction条件具有shared和private的特性,其后结构为(operator: list),其中操作operator用于每次累积时list列出变量的操作。这些操作只针对并形体并行时,它不会影响并形体中该变量的值(包括初始值),但是并形体中该变量值将影响最后该变量在并形体外部的值。该变量将分为两部分,一部分属于shared类型,一部分属于private类型,最终该变量的值就是该变量初始值(在并行之前的值)与并形体中private类型值的operator运算,如果operator为+,则为这些之和。如下面的例子:
// File: ReductionTest.cpp : 定义控制台应用程序的入口点。
#include<omp.h>
#include<iostream>
using namespace std;
//ReductionTest测试
int ReductionTest()
{
cout<<"reduction输出:\n";
inti=0,j=10;
#pragmaomp parallel for reduction(+:j)
for(i=0;i<8;i++)
{
j=2;
cout<<i<<":"<<j<<"\n";
j++;
cout<<i<<":"<<j<<"\n";
}
cout<<"最后j的值为:"<<j<<"\n";
return0;
}
程序运行结果为:
reduction输出:
0:2
0:3
6:2
6:3
2:2
2:3
3:2
3:3
1:2
1:3
5:2
5:3
4:2
4:3
7:2
7:3
最后j的值为:34
从上面的结果可知,变量j在并形体中是以private形式存在,而最后在并形体之间通过操作(+)来完成各个并形体中j的值与初始值(10)的计算,所以最后j的值为:10+(3)+(3)+(3)+(3)+(3)+(3)+(3)+(3)=34。如果操作符是*,则最终j的值为:10*(3)*(3)*(3)*(3)*(3)*(3)*(3)*(3)=65610。
reduction的操作符主要有:
操作符 |
数据类型 |
初始值 |
+ |
整型,浮点型 |
0 |
- |
整型,浮点型 |
0 |
* |
整型,浮点型 |
1 |
& |
整型 |
On |
| |
整型 |
0 |
^ |
整型 |
0 |
&& |
整型 |
1 |
|| |
整型 |
0 |
其中初始值是指在没有为该reduction变量在并形体中初始化时,它默认的值。
如果要列出多个变量,list中用逗号隔开相邻的变量。如果有多种类型的要定义,即有shared又有private等等,相互之间用空格隔开即可。如下格式:
#pragma omp parallel for private(a,b,c) firstprivate(d,e)reduction(+:sum)shedule条件
把并行循环中的计算指定给线程这种方式称为循环队列(loop’s schedule)。对于并行循环中并形体计算量接近的情况,使用默认的队列方式是最优的。但也存在并行循环中每个并行计算量大小不一致的情况,如果计算量大小差距很大,并行程序的执行时间是以最后完成的那个线程为结束标记的,所以如果还采用相同的队列方式,计算量小的线程会先执行完,然后等计算量大的线程执行完,最后才结束并行。在这种情况下,队列分布的不均将会影响整个并行的运行效率,因此,需要去设置其队列选项来控制队列的分布。
schedule条件的格式如下:
schedule(type[,chunk])
其中type有static,dynamic,guided和auto四种,chunk是表示一个并行块的大小。如果需要对1000个循环进行并行,可以将它分成8个并行块(chunk),每个并行块就包括125个循环,则并行块的大小就是125,即chunk size。线程执行的具体对象就是这些并行块chunk。static表示静态分割并行块,在整个并行计算过程中并行块的大小都一样。dynamic则表示动态分割,默认其并行块尺寸为1。guided表示向导性的分割,指定第一个并行块的大小,后面每个并行块的尺寸都会递减,直到最小的并行块尺寸。采用auto或runtime时,不需要设置chunk参数,此时队列类型将由环境变量omp_schedule来控制。
循环结构并行队列过程以及在CPU中执行队列过程如下图所示:
若循环结构中循环次数为100次,通过schedule队列指定每块尺寸为20(即20个循环),则有5个并行块,每个并行块中并形体(一个循环)仍然按串行方式排列。每个并行块对应一个新的线程。若计算机CPU具有4个执行核或4线程,那么每一时刻最多只能执行4个线程,而现在有5个并行块,所以最多只能执行4个并行块,剩下一个并行块就只有在后面,并行计算所耗时间是由最慢的那个线程(并行块)来决定的,所以尽量让这些并行块数目是计算机CPU核心的倍数(1倍或其它整数倍),以充分利用计算机CPU资源。
下面通过一个程序动态设置并行块大小来测试对计算效率的影响,代码如下:
// File: ScheduleTest.cpp
#include<omp.h>
#include<iostream>
using namespace std;
//private测试
int ScheduleTest()
{
cout<<"ScheduleTest输出:\n";
inti=0,j,chunkSize = 1;
doublestarttime,endtime;
cout<<"请输入并行块的大小(-200):\n";
cin>>chunkSize;
starttime=omp_get_wtime();
#pragmaomp parallel for private(j)schedule(static,chunkSize)
for(i=0;i<200;i++)
{
for(j=0;j<100000000;j++);
}
endtime=omp_get_wtime();
cout<<"计算耗时为:"<<endtime-starttime<<"s\n";
return0;
}
分别设置并行块大小为1、2等,分别测试其计算耗时,结果如下表所示:
并行块大小 |
计算耗时(s) |
并行块数目 |
每核平均执行并行块数目 |
空闲线程数 |
并行块大小 |
计算耗时(s) |
并行块数目 |
每核平均执行并行块数目 |
空闲线程数 |
1 |
7.08998 |
200 |
25.0 |
0 |
24 |
8.57893 |
9 |
1.0 |
7 |
2 |
7.2503 |
100 |
12.5 |
4 |
25 |
7.05088 |
8 |
1.0 |
0 |
3 |
7.44965 |
67 |
8.3 |
5 |
26 |
7.25465 |
8 |
1.0 |
0 |
4 |
7.67307 |
50 |
6.3 |
6 |
27 |
7.45207 |
8 |
0.9 |
0 |
5 |
7.09083 |
40 |
5.0 |
0 |
28 |
7.87446 |
8 |
0.9 |
0 |
6 |
8.1865 |
34 |
4.2 |
6 |
29 |
8.4484 |
7 |
0.9 |
1 |
7 |
7.69326 |
29 |
3.6 |
3 |
30 |
8.17421 |
7 |
0.8 |
1 |
8 |
8.57003 |
25 |
3.1 |
7 |
31 |
8.41376 |
7 |
0.8 |
1 |
9 |
7.36662 |
23 |
2.8 |
1 |
32 |
8.62639 |
7 |
0.8 |
1 |
10 |
8.30294 |
20 |
2.5 |
4 |
33 |
9.14871 |
7 |
0.8 |
1 |
11 |
9.01532 |
19 |
2.3 |
5 |
34 |
9.09194 |
6 |
0.7 |
2 |
12 |
8.58991 |
17 |
2.1 |
7 |
35 |
9.32059 |
6 |
0.7 |
2 |
13 |
7.27074 |
16 |
1.9 |
0 |
36 |
9.5623 |
6 |
0.7 |
2 |
14 |
7.70015 |
15 |
1.8 |
1 |
37 |
10.0546 |
6 |
0.7 |
2 |
15 |
8.26512 |
14 |
1.7 |
2 |
38 |
10.1078 |
6 |
0.7 |
2 |
16 |
8.72735 |
13 |
1.6 |
3 |
39 |
10.248 |
6 |
0.6 |
2 |
17 |
9.05444 |
12 |
1.5 |
4 |
40 |
10.472 |
5 |
0.6 |
3 |
18 |
9.52952 |
12 |
1.4 |
4 |
50 |
12.572 |
4 |
0.5 |
4 |
19 |
10.0843 |
11 |
1.3 |
5 |
80 |
20.2732 |
3 |
0.3 |
5 |
20 |
10.5465 |
10 |
1.3 |
6 |
100 |
24.5377 |
2 |
0.3 |
6 |
21 |
10.9686 |
10 |
1.2 |
6 |
150 |
36.5224 |
2 |
0.2 |
6 |
22 |
11.4323 |
10 |
1.1 |
6 |
200 |
48.5702 |
1 |
0.1 |
7 |
23 |
10.2983 |
9 |
1.1 |
7 |
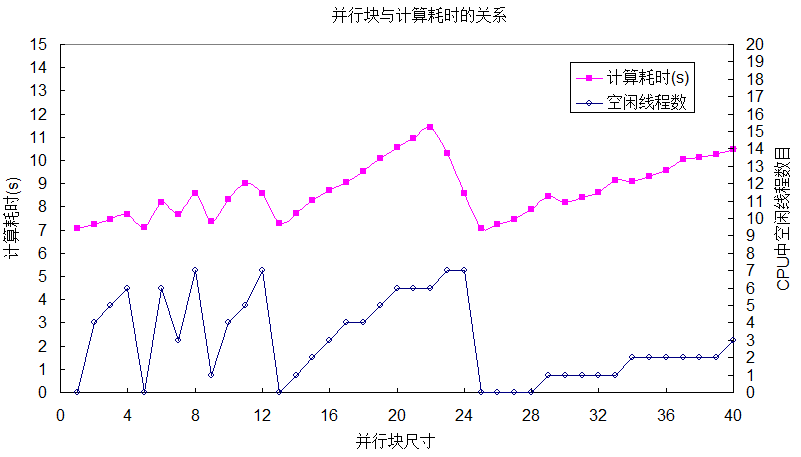
从上图以及测试结果可以得知:在每核平均执行并行块数目大于或等于1.0时,并行块数目对计算效率的影响呈锯齿状形态;当每核平均执行并行块数目小于1.0时,计算效率急剧下降;空闲线程数目越多,计算效率越低。当每核平均执行并行块数目为1,且每个并行块中尺寸均匀相等时,计算效率会提供到极大值,上例中即并行块尺寸为25时。若每个循环的计算量相差不大,建议采用static设置每个并行块尺寸一样。
相关程序源码下载地址:
http://download.csdn.net/detail/xwebsite/3843187