树状数组
http://wtommy.ycool.com/post.766159.html
树状数组
对于数组求和来说树状数组简直太快了!
今天终于领略到了.....!!
先给大家看一个例题,我们队牛人RoBa自创的题目:
题目描述: 给定一个长度为N的数组c[1],c[2]...c[N](N<=10^5),每次可以在这个数组上进行三种操作,"+ k m"表示给c[k]加上m,"- k m"表示给c[k]减去m,"C st end"表示求出c[st]+c[st+1]+..c[end]的值并输出,"Q"表示此次操作结束。 0 < k <= N , 0 <= m < 100 , 0 < st <= end <= N SAMPLE INPUT 3 + 1 2 - 1 2 C 1 1 Q 0 SAMPLE OUTPUT 0 |
算法分析:
如果直接做的话,修改的复杂度是O(1),询问的复杂度是O(N),M次询问的复杂度是M*N.M,N的范围可以有100000以上,所以这样做会超时,但是如果用线段树的话,还是很不错的!
线段树解法分析:
可以看出,这棵树的构造用二分便可以实现.复杂度是2*N.
每个结点用数组a来表示该结点所表示范围内的数据之和.
修改一个位置上数字的值,就是修改一个叶子结点的值,而当程序由叶子结点返回根节点的同时顺便修改掉路径上的结点的a数组的值.
对于询问的回答,可以直接查找i..j范围内的值,遇到分叉时就兵分两路,最后在合起来.也可以先找出0..i-1的值和0..j的值,两个值减一减就行了.后者的实际操作次数比前者小一些.
这样修改与维护的复杂度是logN.询问的复杂度也是logN,对于M次询问,复杂度是MlogN.
然而不难发现,线段树的编程复杂度大,空间复杂度大,时间效率也不高!!!!
所以我们来想用树形数组来实现:
树状数组是一个查询和修改复杂度都为log(n)的数据结构。
假设数组a[1..n],那么查询a[1]+...+a[n]的时间是log级别的,
而且是一个在线的数据结构,支持随时修改某个元素的值,复杂度也为log级别。
那么,何为树形数组呢??
下图中的C数组就是树状数组,a数组是原数组; 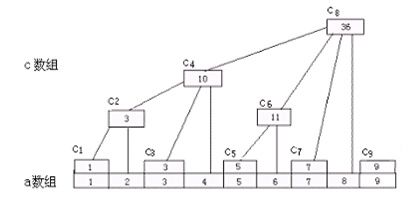
可以发现这些规律:
C1=a1
C2=a1+a2
C3=a3
C4=a1+a2+a3+a4
C5=a5
……
C8=a1+a2+a3+a4+a5+a6+a7+a8
……
C2^n=a1+a2+….+a2^n
对于序列a,我们设一个数组C定义C[t] = a[t – 2^k + 1] + … + a[t],k为t在二进制下末尾0的个数。
K的计算可以这样:
2^k=t and (t xor (t-1))
以6为例
(6)10=(0110)2
xor 6-1=(5)10=(0101)2
(0011)2
and (6)10=(0110)2
(0010)2
所以问题变的很简单,重要写几个函数就可以了;
求2^k的函数代码如下:
int Lowbit(int t) { return t & ( t ^ ( t - 1 ) ); } |
求1 -- end和的函数代码如下:
int Sum(int end) { int sum = 0; while(end > 0) { sum += in[end]; end -= Lowbit(end); } return sum; } |
对某位进行操作函数如下(以加法为例)
void plus(int pos , int num) { while(pos <= n) { in[pos] += num; pos += Lowbit(pos); } } |
有了这三个函数整个树形数组也就基本构建成功啦!!
对于刚才的一题,每次修改与询问都是对C数组做处理.空间复杂度有3N降为N,时间效率也有所提高.编程复杂度更是降了不少.