DES加解密算法Qt实现
【声明】
(1) 本文源码
大部分源码来自:DES算法代码。在此基础上,利用Qt编程进行了改写,实现了DES加解密算法,并添加了文件加解密功能。在此对署名为bengold1979的网友表示感谢!本文是对DES算法代码一文代码的具体描述。该源码仅供学习交流,请勿用于商业目的。
(2) 图片及描述
图片及部分解析来自
http://zh.wikipedia.org/wiki/%E8%B3%87%E6%96%99%E5%8A%A0%E5%AF%86%E6%A8%99%E6%BA%96。
【简介】
DES(Data Encryption Standard,资料加密标准),是一种使用密钥加密的块密码,1976年被美国联邦政府的国家标准局确定为联邦资料处理标准(FIPS),随后在国际上广泛流传开来。它基于使用56位密钥的对称算法。与其它块密码相似,DES自身并不是加密的实用手段,而必须以某种工作模式进行实际操作。FIPS-81确定了DES使用的几种模式[32] 。FIPS-74包括了更多关于DES使用的讨论。
【算法描述】
DES是一种典型的块密码—一种将固定长度的平文通过一系列复杂的操作变成同样长度的密文的算法。对DES而言,块长度为64位。同时,DES使用密钥来自定义变换过程,因此算法认为只有持有加密所用的密钥的用户才能解密密文。密钥表面上是64位的,然而只有其中的56位被实际用于算法,其余8位可以被用于奇偶校验,并在算法中被丢弃。因此,DES的有效密钥长度为56位,通常称DES的密钥长度为56位。
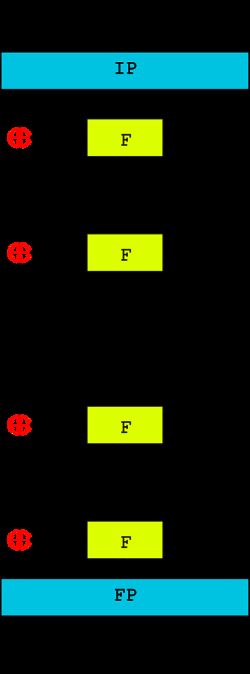
DES算法整体结构图,如图1所示:
图1 DES整体结构图
有16个相同的处理过程,称为“回次”(round),并在首位各有一次置换,称为IP与FP(或称IP-1,FP为IP的反函数吗,即IP“撤销”FP的操作,反之亦然)。IP和FP几乎没有密码学上的重要性,为了在1970年代中期的硬件上简化输入输出数据库的过程而被显式的包括在标准中。
在主处理回次前,数据块被分成两个32位的半块,并被分别处理;这种交叉的方式被称为费斯妥结构。费斯妥结构保证了加密和解密过程足够相似—唯一的区别在于子密钥在解密时是以反向的顺序应用的,而剩余部分均相同。这样的设计大大简化了算法的实现,尤其是硬件实现,因为没有区分加密和解密算法的需要。
图中的⊕符号代表异或(XOR)操作。“F函数”将数据半块与某个子密钥进行处理。然后,一个F函数的输出与另一个半块异或之后,再与原本的半块组合并交换顺序,进入下一个回次的处理。在最后一个回次完成时,两个半块不必交换顺序,这是费斯妥结构的一个特点,以保证加解密的过程相似。
【算法解析】
1 常量定义
下述定义,实际上是一个矢量,而非矩阵。详细请参考:
http://zh.wikipedia.org/wiki/DES%E8%A1%A5%E5%85%85%E6%9D%90%E6%96%99#.E9.80.89.E6.8B.A9.E7.BD.AE.E6.8D.A22.28PC-2.29
IP表
const int DES::IP_Table[] =
{
58, 50, 42, 34, 26, 18, 10, 2, 60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6, 64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1, 59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5, 63, 55, 47, 39, 31, 23, 15, 7,
};
// final permutation IP^-1
const int DES::IPR_Table[] =
{
40, 8, 48, 16, 56, 24, 64, 32, 39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30, 37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28, 35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26, 33, 1, 41, 9, 49, 17, 57, 25
};
Expand Array
const int DES::E_Table[48] =
{
32,1,2,3,4,5,
4,5,6,7,8,9,
8,9,10,11,12,13,
12,13,14,15,16,17,
16,17,18,19,20,21,
20,21,22,23,24,25,
24,25,26,27,28,29,
28,29,30,31,32,1
};
P转换表
const int DES::P_Table[32] =
{
16,7,20,21,
29,12,28,17,
1,15,23,26,
5,18,31,10,
2,8,24,14,
32,27,3,9,
19,13,30,6,
22,11,4,25
};
PC1表
const int DES::PC1_Table[56] =
{
57,49,41,33,25,17,9,
1,58,50,42,34,26,18,
10,2,59,51,43,35,27,
19,11,3,60,52,44,36,
63,55,47,39,31,33,15,
7,62,54,46,38,30,22,
14,6,61,53,45,37,29,
21,13,5,28,20,12,4
};
PC2表
const int DES::PC2_Table[48] =
{
14,17,11,24,1,5,
3,28,15,6,21,10,
23,19,12,4,26,8,
16,7,27,20,13,2,
41,52,31,37,47,55,
30,40,51,45,33,48,
44,49,39,56,34,53,
46,42,50,36,29,32
};
循环移位表
const int DES::LOOP_Table[16] =
{
1,1,2,2,2,2,2,2,1,2,2,2,2,2,2,1
};
S-Box
const int DES::S_Box[8][4][16] =
{
{
{14,4,13,1,2,15,11,8,3,10,6,12,5,9,0,7},
{0,15,7,4,14,2,13,1,10,6,12,11,9,5,3,8},
{4,1,14,8,13,6,2,11,15,12,9,7,3,10,5,0},
{15,12,8,2,4,9,1,7,5,11,3,14,10,0,6,13}
},
{
{15,1,8,14,6,11,3,4,9,7,2,13,12,0,5,10},
{3,13,4,7,15,2,8,14,12,0,1,10,6,9,11,5},
{0,14,7,11,10,4,13,1,5,8,12,6,9,3,2,15},
{13,8,10,1,3,15,4,2,11,6,7,12,0,5,14,9}
},
{
{10,0,9,14,6,3,15,5,1,13,12,7,11,4,2,8},
{13,7,0,9,3,4,6,10,2,8,5,14,12,11,15,1},
{13,6,4,9,8,15,3,0,11,1,2,12,5,10,14,7},
{1,10,13,0,6,9,8,7,4,15,14,3,11,5,2,12}
},
{
{7,13,14,3,0,6,9,10,1,2,8,5,11,12,4,15},
{13,8,11,5,6,15,0,3,4,7,2,12,1,10,14,9},
{10,6,9,0,12,11,7,13,15,1,3,14,5,2,8,4},
{3,15,0,6,10,1,13,8,9,4,5,11,12,7,2,14}
},
{
{2,12,4,1,7,10,11,6,8,5,3,15,13,0,14,9},
{14,11,2,12,4,7,13,1,5,0,15,10,3,9,8,6},
{4,2,1,11,10,13,7,8,15,9,12,5,6,3,0,14},
{11,8,12,7,1,14,2,13,6,15,0,9,10,4,5,3}
},
{
{12,1,10,15,9,2,6,8,0,13,3,4,14,7,5,11},
{10,15,4,2,7,12,9,5,6,1,13,14,0,11,3,8},
{9,14,15,5,2,8,12,3,7,0,4,10,1,13,11,6},
{4,3,2,12,9,5,15,10,11,14,1,7,6,0,8,13}
},
{
{4,11,2,14,15,0,8,13,3,12,9,7,5,10,6,1},
{13,0,11,7,4,9,1,10,14,3,5,12,2,15,8,6},
{1,4,11,13,12,3,7,14,10,15,6,8,0,5,9,2},
{6,11,13,8,1,4,10,7,9,5,0,15,14,2,3,12}
},
{
{13,2,8,4,6,15,11,1,10,9,3,14,5,0,12,7},
{1,15,13,8,10,3,7,4,12,5,6,11,0,14,9,2},
{7,11,4,1,9,12,14,2,0,6,10,13,15,3,5,8},
{2,1,14,7,4,10,8,13,15,12,9,0,3,5,6,11}
}
};
2 费斯妥函数(F函数)
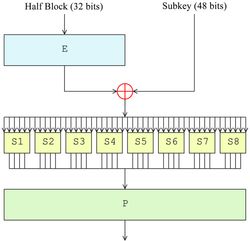
图2中显示了费斯妥函数(F函数)的过程。其每次对半块(32位)进行操作,并包括四个步骤:
图2 费斯妥函数
(1) 扩张—用扩张置换(图中的E)将32位的半块扩展到48位,其输出包括8个6位的块,每块包含4位对应的输入位,加上两个邻接的块中紧邻的位。
void DES::Transform(Bit *Out, Bit *In, const int *Table, int len)
{
bool Tmp[256];
for(int i=0; i<len; ++i)
Tmp[i] = In[ Table[i]-1 ];
memcpy(Out, Tmp, len);
}
Transform(MR, In, E_Table, 48);
(2) 与密钥混合—用异或操作将扩张的结果和一个子密钥进行混合。16个48位的子密钥—每个用于一个回次的F变换—是利用密钥调度从主密钥生成的(见下文)。
void DES::Xor(Bit *InA, const Bit *InB, int len)
{
for(int i = 0; i < len; ++i)
InA[i] ^= InB[i];
}
(3) S盒—在与子密钥混合之后,块被分成8个6位的块,然后使用“S盒”,或称“置换盒”进行处理。8个S盒的每一个都使用以查找表方式提供的非线性的变换将它的6个输入位变成4个输出位。S盒提供了DES的核心安全性—如果没有S盒,密码会是线性的,很容易破解。
void DES::S_func(Bit Out[], const Bit In[])
{
for(int i=0,j,k; i<8; ++i,In+=6,Out+=4)
{
j = (In[0]<<1) + In[5];
k = (In[1]<<3) + (In[2]<<2) + (In[3]<<1) + In[4]; //组织SID下标
for(int l=0; l<4; ++l) //把相应4bit赋值
Out[l] = (S_Box[i][j][k]>>(3 - l)) & 1;
}
}
(4) 置换—最后,S盒的32个输出位利用固定的置换,“P置换”进行重组。这个设计是为了将每个S盒的4位输出在下一回次的扩张后,使用4个不同的S盒进行处理。S盒,P置换和E扩张各自满足了克劳德•香农在1940年代提出的实用密码所需的必要条件,“混淆和扩散”。
void DES::F_func(Bit In[32], const Bit Ki[48])
{
bool MR[48];
Transform(MR, In, E_Table, 48);
Xor(MR, Ki, 48);
S_func(In, MR);
Transform(In, In, P_Table, 32);
}
3 密钥调度
如图3所示,首先,使用选择置换1(PC-1)从64位输入密钥中选出56位的密钥—剩下的8位要么直接丢弃,要么作为奇偶校验位。然后,56位分成两个28位的半密钥;每个半密钥接下来都被分别处理。在接下来的回次中,两个半密钥都被左移1或2位(由回次数决定),然后通过选择置换2(PC-2)产生48位的子密钥—每个半密钥24位。移位(图中由<<标示)表明每个子密钥中使用了不同的位,每个位大致在16个子密钥中的14个出现。
图3 密钥调度
void DES::ByteToBit(Bit *Out, const unsigned char *In, int bits)
{
for(int i = 0; i < bits; ++i)
Out[i] = (In[i>>3]>>(7 - (i&7))) & 1;
}
void DES::RotateL(Bit *In, int len, int loop)
{
Bit Tmp[256];
memcpy(Tmp, In, loop);
memcpy(In, In+loop, len-loop);
memcpy(In+len-loop, Tmp, loop);
}
void DES::SetSubKey(PSubKey pSubKey, const unsigned char Key[])
{
bool K[64], *KL=&K[0], *KR=&K[28];
ByteToBit(K, Key, 64);
Transform(K, K, PC1_Table, 56);
for(int i=0; i<16; ++i) {
RotateL(KL, 28, LOOP_Table[i]);
RotateL(KR, 28, LOOP_Table[i]);
Transform((*pSubKey)[i], K, PC2_Table, 48);
}
}
4 明文填充
DES加解密以8位为单位进行,如果输入明文不是8位,则利用填充函数进行填充为8的整数倍。
bool DES::RunPad(int nType, const unsigned char *In, unsigned datalen, unsigned char *Out, unsigned &padlen)
{
if (nType < PAD_ISO_1 || nType > PAD_PKCS_7)
return false;
if (In == NULL || datalen < 0 || Out == NULL)
return false;
int res = (datalen & 0x00000007);
if (res == 0)
{
padlen = datalen;
memcpy(Out, In, datalen);
return true;
}
padlen = (datalen+8-res);
memcpy(Out,In,datalen);
if(nType == PAD_ISO_1)
{
memset(Out+datalen,0x00,8-res);
}
else if(nType == PAD_ISO_2)
{
memset(Out+datalen,0x80,1);
memset(Out+datalen,0x00,7-res);
}
else if(nType == PAD_PKCS_7)
{
memset(Out+datalen,0x00,8-res);
}
else
{
return false;
}
return true;
}
5 DES运算单元(详见【算法描述】)
void DES::ByteToBit(Bit *Out, const unsigned char *In, int bits)
{
for(int i = 0; i < bits; ++i)
Out[i] = (In[i>>3]>>(7 - (i&7))) & 1;
}
void DES::BitToByte(unsigned char *Out, const Bit *In, int bits)
{
memset(Out, 0, bits>>3);
for(int i = 0; i < bits; ++i)
Out[i>>3] |= In[i]<<(7 - (i&7));
}
void DES::DES_Unit(unsigned char Out[], const unsigned char In[], const PSubKey pSubKey, bool Type)
{
bool M[64], tmp[32], *Li=&M[0], *Ri=&M[32];
ByteToBit(M, In, 64);
Transform(M, M, IP_Table, 64);
if( Type == ENCRYPT )
{
for(int i=0; i<16; ++i)
{
memcpy(tmp, Ri, 32); //Ri[i-1] 保存
F_func(Ri, (*pSubKey)[i]); //Ri[i-1]经过转化和SBox输出为P
Xor(Ri, Li, 32); //Ri[i] = P XOR Li[i-1]
memcpy(Li, tmp, 32); //Li[i] = Ri[i-1]
}
}
else
{
for(int i=15; i>=0; --i)
{
memcpy(tmp, Ri, 32); //Ri[i-1] 保存
F_func(Ri, (*pSubKey)[i]); //Ri[i-1]经过转化和SBox输出为P
Xor(Ri, Li, 32); //Ri[i] = P XOR Li[i-1]
memcpy(Li, tmp, 32); //Li[i] = Ri[i-1]
}
}
RotateL(M,64,32); //Ri与Li换位重组M
Transform(M, M, IPR_Table, 64); //最后结果进行转化
BitToByte(Out, M, 64); //组织成字符
}
6 DES加解密
(1) DES和3DES
DES,在加解密时,只运行DES运算单元一次。3DES,在加解密时,运行DES运算单元3次。
(2) 工作模式
(a) 电子密码本模式(EBC)
最古老,最简单的模式,将加密的数据分成若干组,每组的大小跟加密密钥长度相同;然后每组都用相同的密钥加密, 比如DES算法, 如果最后一个分组长度不够64位,要补齐64位。
定义
Enc(X,Y)是加密函数
Dec(X,Y)是解密函数
Key是加密密钥;
Pi ( i = 0,1…n)是明文块,大小为64bit;
Ci ( i = 0,1…n)是密文块,大小为64bit;
ECB加密算法可表示为:
Ci = Enc(Key, Pi)
ECB解密算法可以表示为:
Pi = Dec(Key,Ci)
算法特点
每次Key、明文、密文的长度都必须是64位;
数据块重复排序不需要检测;
相同的明文块(使用相同的密钥)产生相同的密文块,容易遭受字典攻击;
一个错误仅仅会对一个密文块产生影响。
(b) 加密块链模式(CBC)
与ECB模式最大的不同是加入了初始向量。
定义
Enc(X,Y)是加密函数
Dec(X,Y)是解密函数
Key是加密密钥;
Pi ( i = 0,1…n)是明文块,大小为64bit;
Ci ( i = 0,1…n)是密文块,大小为64bit;
XOR(X,Y)是异或运算;
IV是初始向量(一般为64位);
ECB加密算法可表示为:
C0 = Enc(Key, XOR(IV, P0)
Ci = Enc(Key, XOR(Ci-1, Pi)
ECB解密算法可以表示为:
P0 = XOR(IV, Dec(Key, C0))
Pi = XOR(Ci-1, Dec(Key,Ci))
算法特点
每次加密的密文长度为64位(8个字节);
当相同的明文使用相同的密钥和初始向量的时候CBC模式总是产生相同的密文;
密文块要依赖以前的操作结果,所以,密文块不能进行重新排列;
可以使用不同的初始化向量来避免相同的明文产生相同的密文,一定程度上抵抗字典攻击;
一个错误发生以后,当前和以后的密文都会被影响。
(c) 加密反馈模式(CFB)
加密反馈模式克服了需要等待8个字节才能加密的缺点,它采用了分组密码作为流密码的密钥流生成器。
定义
Enc(X,Y)是加密函数
Dec(X,Y)是解密函数
Key是加密密钥;
Pi ( i = 0,1…n)是明文块,大小为64bit;
Ci ( i = 0,1…n)是密文块,大小为64bit;
Si ( i = 0,1…n),大小为8bit,n个连续的Si组成加密位移寄存器,一般n=8;
Oi = Enc(Key, Si);
Lef(x) 为取数据x的最左8个bit位;
A(x,y)为合并x左移8位,空位用y填充
CFB加密算法可表示为:
S0 = IV;
Oi = Enc(Key, Si);
Ci = XOR( Ci, Lef(Oi));
Si = A(Si-1, Ci);
CFB解密算法可表示为:
S0 = IV;
Oi = Enc(Key, Si);
Ci = XOR( Ci, Lef(Oi));
Si = A(Si-1, Ci);
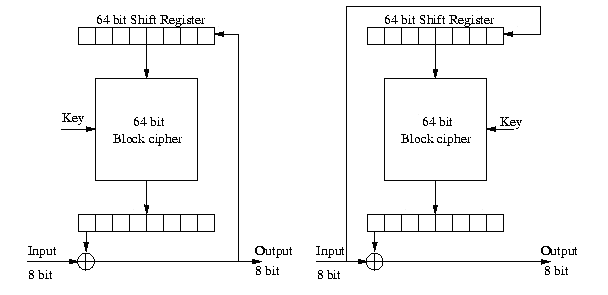
图示:
每次加密的Pi和Ci不大于64位;
加密算法和解密算法相同,不能适用于公钥算法;
使用相同的密钥和初始向量的时候,相同明文使用CFB模式加密输出相同的密文;
可以使用不同的初始化变量使相同的明文产生不同的密文,防止字典攻击;
加密强度依赖于密钥长度;
加密块长度过小时,会增加循环的数量,导致开销增加;
加密块长度应时8位的整数倍(即字节为单位);
一旦某位数据出错,会影响目前和其后8个块的数据。
(d) 输出反馈模式(OFB)
与CFB模式不同之处在于, 加密位移寄存器与密文无关了,仅与加密key和加密算法有关;做法是不再把密文输入到加密移位寄存器,而是把输出的分组密文(Oi)输入到一位寄存器。
定义
Enc(X,Y)是加密函数
Dec(X,Y)是解密函数
Key是加密密钥;
Pi ( i = 0,1…n)是明文块,大小为64bit;
Ci ( i = 0,1…n)是密文块,大小为64bit;
Si ( i = 0,1…n),大小为8bit,n个连续的Si组成加密位移寄存器,一般n=8;
Oi = Enc(Key, Si);
Lef(x) 为取数据x的最左8个bit位;
A(x,y)为合并x左移8位,空位用y填充
CFB加密算法可表示为:
S0 = IV;
Oi = Enc(Key, Si);
Ci = XOR( Ci, Lef(Oi));
Si = A(Si-1, Oi); 注意这里与CFB模式的不同
CFB解密算法可表示为:
S0 = IV;
Oi = Enc(Key, Si);
Ci = XOR( Ci, Lef(Oi));
Si = A(Si-1, Oi);
算法特点
与CFB类似,以下都是不同之处;
因为密文没有参与链操作,所以使得OFB模式更容易受到攻击;
不会进行错误传播,某位密文发生错误,只会影响该位对应的明文,而不会影响别的位;
不是自同步的,如果加密和解密两个操作失去同步,那么系统需要重新初始化;
每次重新同步时,应使用不同的初始向量。可以避免产生相同的比特流,避免”已知明文”攻击。
bool DES::RunDes(bool bType,bool bMode,const unsigned char *In,
unsigned char *Out,unsigned datalen,const unsigned char *Key,unsigned keylen)
{
//判断输入合法性
if(!(In && Out && Key && datalen && keylen>=8))
return false;
unsigned char inbuf[datalen + 8];
memset(inbuf, 0x00, sizeof(inbuf));
memcpy(inbuf, In, datalen);
unsigned char* tempBuf;
unsigned padlen = datalen;
//只处理8的整数倍,不足长度自己填充
if(datalen & 0x00000007)
{
if (!RunPad(PAD_PKCS_7, In, datalen, inbuf, padlen))
return false;
tempBuf = inbuf;
}
else
{
tempBuf = inbuf;
}
bool m_SubKey[3][16][48]; //秘钥
//构造并生成SubKeys
char nKey = (keylen>>3)>=3 ? 3: (keylen>>3);
for(int i=0;i<nKey;i++)
{
SetSubKey(&m_SubKey[i],&Key[i<<3]);
}
if(bMode == ECB) //ECB模式
{
if(nKey == 1) //单Key
{
for(int i=0,j = padlen>>3;i<j;++i,Out+=8,tempBuf+=8)
{
DES_Unit(Out,tempBuf,&m_SubKey[0],bType);
}
}
else
if(nKey == 2) //3DES 2Key
{
for(int i=0,j = padlen>>3;i<j;++i,Out+=8,tempBuf+=8)
{
DES_Unit(Out,tempBuf,&m_SubKey[0],bType);
DES_Unit(Out,Out,&m_SubKey[1],!bType);
DES_Unit(Out,Out,&m_SubKey[0],bType);
}
}
else //3DES 3Key
{
for(int i=0,j=padlen>>3;i<j;++i,Out+=8,tempBuf+=8)
{
DES_Unit(Out,tempBuf,&m_SubKey[bType? 2 : 0],bType);
DES_Unit(Out,Out,&m_SubKey[1],!bType);
DES_Unit(Out,Out,&m_SubKey[bType? 0 : 2],bType);
}
}
}
else //CBC模式
{
unsigned char cvec[8] = ""; //扭转向量
unsigned char cvin[8] = ""; //中间变量
if(nKey == 1) //单Key
{
for(int i=0,j=padlen>>3;i<j;++i,Out+=8,tempBuf+=8)
{
if(bType == ENCRYPT)
{
for(int j=0;j<8;++j) //将输入与扭转变量异或
{
cvin[j] = tempBuf[j] ^ cvec[j];
}
}
else
{
memcpy(cvin,tempBuf,8);
}
DES_Unit(Out,cvin,&m_SubKey[0],bType);
if(bType == ENCRYPT)
{
memcpy(cvec,Out,8); //将输出设定为扭转变量
}
else
{
for(int j=0;j<8;++j) //将输出与扭转变量异或
{
Out[j] = Out[j] ^ cvec[j];
}
memcpy(cvec,cvin,8); //将输入设定为扭转变量
}
}
}
else
if(nKey == 2) //3DES CBC 2Key
{
for(int i=0,j=padlen>>3;i<j;++i,Out+=8,tempBuf+=8)
{
if(bType == ENCRYPT)
{
for(int j=0;j<8;++j) //将输入与扭转变量异或
{
cvin[j] = tempBuf[j] ^ cvec[j];
}
}
else
{
memcpy(cvin,tempBuf,8);
}
DES_Unit(Out,cvin,&m_SubKey[0],bType);
DES_Unit(Out,Out,&m_SubKey[1],!bType);
DES_Unit(Out,Out,&m_SubKey[0],bType);
if(bType == ENCRYPT)
{
memcpy(cvec,Out,8); //将输出设定为扭转变量
}
else
{
for(int j=0;j<8;++j) //将输出与扭转变量异或
{
Out[j] = Out[j] ^ cvec[j];
}
memcpy(cvec,cvin,8); //将输入设定为扭转变量
}
}
}
else //3DES CBC 3Key
{
for(int i=0,j=padlen >>3;i<j;++i,Out+=8,tempBuf+=8)
{
if(bType == ENCRYPT)
{
for(int j=0;j<8;++j) //将输入与扭转变量异或
{
cvin[j] = tempBuf[j] ^ cvec[j];
}
}
else
{
memcpy(cvin,tempBuf,8);
}
DES_Unit(Out,cvin,&m_SubKey[bType ? 2 : 0],bType);
DES_Unit(Out,Out,&m_SubKey[1],!bType);
DES_Unit(Out,Out,&m_SubKey[bType ? 0 : 2],bType);
if(bType == ENCRYPT)
{
memcpy(cvec,Out,8); //将输出设定为扭转变量
}
else
{
for(int j=0;j<8;++j) //将输出与扭转变量异或
{
Out[j] = Out[j] ^ cvec[j];
}
memcpy(cvec,cvin,8); //将输入设定为扭转变量
}
}
}
}
return true;
}
【算法举例】
bool DES::RunDesEncode(const unsigned char *In, unsigned char *Out, const unsigned char *Key,
unsigned datalen, unsigned keylen, bool bMode)
{
return RunDes(ENCRYPT, bMode, In, Out, datalen, Key, keylen);
}
bool DES::RunDesDecode(const unsigned char* In, unsigned char* Out, const unsigned char* Key,
unsigned datalen, unsigned keylen, bool bMode)
{
return RunDes(DECRYPT, bMode, In, Out, datalen, Key, keylen);
}
DES des;
//-1-
printf("-----------------------\n");
unsigned char in1[]={'a','b','c','d','e','f','g','h'};
unsigned char key1[24]={'q','w','r','t','y','u','0','b','v','s','a','z','l',';','y','5','?','3','n','m','3','0','a','q'};
unsigned char out1[8];
unsigned char result1[8];
for(size_t i=0; i<sizeof(in1); i++)
printf("%c", in1[i]);
printf("\n");
//des.RunDesEncode(in1, out1, key1, 8, 24, CBC);
//des.RunDesEncode(in1, out1, key1, 8, 24);
des.RunDesEncode(in1, out1, key1);
for(size_t i=0; i<sizeof(out1); i++)
printf("%c", out1[i]);
printf("\n");
//des.RunDesDecode(out1, result1, key1, 8, 24, CBC);
//des.RunDesDecode(out1, result1, key1, 8, 24);
des.RunDesDecode(out1, result1, key1);
for(size_t i=0; i<sizeof(result1); i++)
printf("%c", result1[i]);
printf("\n");
for(int i=0; i<8; i++)
assert((in1[i] == result1[i]));
【文件加密】
本文仅分析DES算法本身,不就DES文件加密进行分析。源码中的文件加密功能仅供测试用。实际使用时,文件加密可使用多线程,要考虑加锁、明文字节填充等问题。
【源码下载】
http://download.csdn.net/detail/tandesir/4613526
【参考文献】
1 http://zh.wikipedia.org/wiki/%E8%B3%87%E6%96%99%E5%8A%A0%E5%AF%86%E6%A8%99%E6%BA%96
2 http://blog.csdn.net/bengold1979/article/details/2208930
3 http://blog.csdn.net/iamfafa/article/details/6364369
转载请标明出处,仅供学习交流,勿用于商业目的
Copyright @ http://blog.csdn.net/tandesir