VS2012下基于Glut 矩阵变换示例程序:
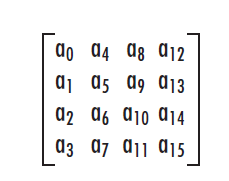
也可以使用我们自己的矩阵运算来实现OpenGL下的glTranslatef相应的旋转变换。需要注意的是OpenGL下的矩阵是列优先存储的。
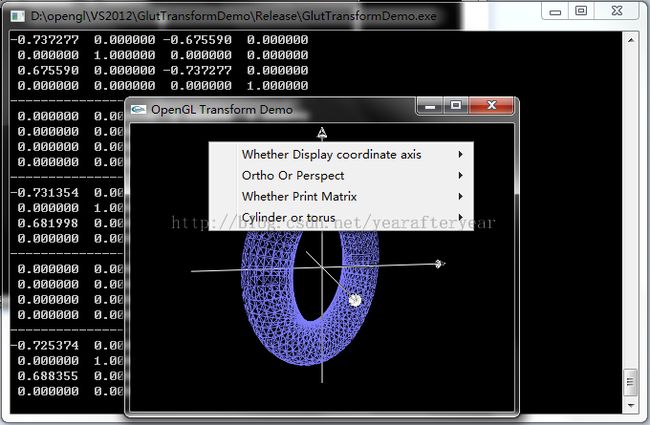
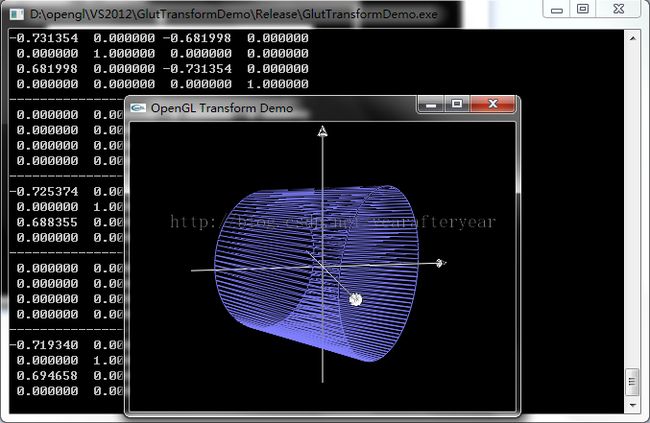
示例通过矩阵运算使得圆柱或者甜圈自动绕Y轴旋转,可以单击鼠标右键来弹出菜单选择是否显示坐标轴、正视图或者是透视图、是否打印变换矩阵、显示圆柱还是甜圈。程序用到math3d中的矩阵相关函数。由于绘制的坐标轴并未参加矩阵变换,在运行过程中会发现坐标轴并不会在定时器作用下不断旋转。
源代码:
GlutTransformDemo
// GlutTransformDemo.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include <gl/glut.h>
#include <math.h>
#include "math3d.h"
//圆周率宏
#define GL_PI 3.1415f
//获取屏幕的宽度
GLint SCREEN_WIDTH=0;
GLint SCREEN_HEIGHT=0;
//设置程序的窗口大小
GLint windowWidth=400;
GLint windowHeight=300;
//绕x轴旋转角度
GLfloat xRotAngle=0.0f;
//绕y轴旋转角度
GLfloat yRotAngle=0.0f;
//受支持的点大小范围
GLfloat sizes[2];
//受支持的点大小增量
GLfloat step;
//最大的投影矩阵堆栈深度
GLint iMaxProjectionStackDepth;
//最大的模型视图矩阵堆栈深度
GLint iMaxModeviewStackDepth;
//最大的纹理矩阵堆栈深度
GLint iMaxTextureStackDepth;
GLint iCoordinateaxis=2;//是否显示坐标轴
GLint iProjectionMode=1;//投影模式
GLint iPrintMatrix=1;//是否打印变换矩阵
GLint iCylinder=1;//显示圆柱还是甜圈
void changSize(GLint w,GLint h);
void DrawTorus(M3DMatrix44f mTransform){
// 大圆只存在于 xy 平面,
// 小圆存在于 xyz 空间中,
// 其圆心是大圆圆周上的点。
// 小圆环大圆半径方向为起始旋转一周形成的。
// 由于 z 轴垂直于 xy 平面,
// 又因为大圆的半径位于 xy 平面,
// 因此,z 轴垂直于大圆的半径(垂直于面,垂直于线),
// 因此,z 轴与大圆的半径方向是正交的。
// 小圆位于 z 轴与大圆半径方向形成的平面,
// 后面计算具体点的位置是基于上面的描述。
// 大圆半径
GLfloat majorRadius = 55.0f;
// 小圆半径
GLfloat minorRadius = 15.0f;
// 大圆圆周被切分的点数
GLint numMajor = 50;
// 小圆圆周被切分的点数
GLint numMinor = 20;
M3DVector3f objectVertex; // Vertex in object/eye space
M3DVector3f transformedVertex; // New Transformed vertex
// 每个点对应的弧度数
double majorStep = 2.0f*M3D_PI / numMajor;
double minorStep = 2.0f*M3D_PI / numMinor;
int i, j;
// 对于大圆上的点进行迭代
for (i=0; i<numMajor; ++i)
{
// 第一个点对应的弧度
double a0 = i * majorStep;
// 第二个点对应的弧度
double a1 = a0 + majorStep;
// 第一个点在 x 与 y 轴上的单位长度
GLfloat x0 = (GLfloat) cos(a0);
GLfloat y0 = (GLfloat) sin(a0);
// 第二个点在 x 与 y 轴上的单位长度
GLfloat x1 = (GLfloat) cos(a1);
GLfloat y1 = (GLfloat) sin(a1);
glBegin(GL_TRIANGLE_STRIP);
// 对小圆上的点进行迭代
for (j=0; j<=numMinor; ++j)
{
// 小圆上点对应的弧度
double b = j * minorStep;
// 小圆上点在半径方向的单位长度
GLfloat c = (GLfloat) cos(b);
// 小圆上点,在xy 平面的分量长度
GLfloat r = minorRadius * c + majorRadius;
// 小圆上点在 z 轴上的长度
GLfloat z = minorRadius * (GLfloat) sin(b);
// 小圆上点坐标确认的过程:将该点分为在 z 轴 与 大圆半径方向,由于大圆半径只存在于 xy 平面,就相对容易求到 x , y 坐标。
// First point
objectVertex[0] = x0*r;// 小圆上点对应的 x 坐标
objectVertex[1] = y0*r;// 小圆上点对应的 y 坐标
objectVertex[2] = z; // 小圆上点对应的 z 坐标
m3dTransformVector3(transformedVertex, objectVertex, mTransform);
glVertex3fv(transformedVertex);
// Second point
objectVertex[0] = x1*r;
objectVertex[1] = y1*r;
objectVertex[2] = z;
m3dTransformVector3(transformedVertex, objectVertex, mTransform);
glVertex3fv(transformedVertex);
}
glEnd();
}
}
void DrawCylinder(M3DMatrix44f mTransform){
// 大圆半径
GLfloat majorRadius = 55.0f;
// 大圆圆周被切分的点数
GLint numMajor = 100;
M3DVector3f objectVertex; // Vertex in object/eye space
M3DVector3f transformedVertex; // New Transformed vertex
// 每个点对应的弧度数
double majorStep = 2.0f*M3D_PI / numMajor;
glBegin(GL_TRIANGLE_STRIP);
// 对于大圆上的点进行迭代
for (int i=0; i<=numMajor; ++i)
{
// 第一个点对应的弧度
double a0 = i * majorStep;
// 第二个点对应的弧度
double a1 = a0 - majorStep;
// 第一个点在 x 与 y 轴上的单位长度
GLfloat x0 = (GLfloat) cos(a0);
GLfloat y0 = (GLfloat) sin(a0);
// 第二个点在 x 与 y 轴上的单位长度
GLfloat x1 = (GLfloat) cos(a1);
GLfloat y1 = (GLfloat) sin(a1);
// First point
objectVertex[0] = x0*majorRadius;// 小圆上点对应的 x 坐标
objectVertex[1] = y0*majorRadius;// 小圆上点对应的 y 坐标
objectVertex[2] = 50.0f; // 小圆上点对应的 z 坐标
m3dTransformVector3(transformedVertex, objectVertex, mTransform);
glVertex3fv(transformedVertex);
// Second point
objectVertex[0] = x1*majorRadius;
objectVertex[1] = y1*majorRadius;
objectVertex[2] = -50.0f;
m3dTransformVector3(transformedVertex, objectVertex, mTransform);
glVertex3fv(transformedVertex);
}
glEnd();
}
//菜单回调函数
void processMenu(int value){
switch(value){
case 1:
iCoordinateaxis=1;
break;
case 2:
iCoordinateaxis=2;
break;
case 3:
iProjectionMode=1;
//强制调用窗口大小变化回调函数,更改投影模式为正交投影
changSize(glutGet(GLUT_WINDOW_WIDTH),glutGet(GLUT_WINDOW_HEIGHT));
break;
case 4:
iProjectionMode=2;
//强制调用窗口大小变化回调函数,更改投影模式为透视投影
changSize(glutGet(GLUT_WINDOW_WIDTH),glutGet(GLUT_WINDOW_HEIGHT));
break;
case 5:
iPrintMatrix=1;
break;
case 6:
iPrintMatrix=2;
break;
case 7:
iCylinder=1;
break;
case 8:
iCylinder=2;
break;
default:
break;
}
//重新绘制
glutPostRedisplay();
}
//显示回调函数
void renderScreen(void){
M3DMatrix44f transformationMatrix; // Storeage for rotation matrix
static GLfloat yRot = 0.0f; // Rotation angle for animation
yRot += 0.5f;
//将窗口颜色清理为黑色
glClearColor(0.0f, 0.0f, 0.0f, 0.0f);
//把整个窗口清理为当前清理颜色:黑色;清除深度缓冲区。
glClear(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT);
//将当前Matrix状态入栈
glPushMatrix();
if(2==iProjectionMode)
glTranslatef(0.0f, 0.0f, -250.0f); //透视投影为便于观察整个坐标系往内移动250个单位
//坐标系绕x轴旋转xRotAngle
glRotatef(xRotAngle,1.0f,0.0f,0.0f);
//坐标系绕y轴旋转yRotAngle
glRotatef(yRotAngle,0.0f,1.0f,0.0f);
//进行平滑处理
glEnable(GL_POINT_SMOOTH);
glHint(GL_POINT_SMOOTH,GL_NICEST);
glEnable(GL_LINE_SMOOTH);
glHint(GL_LINE_SMOOTH,GL_NICEST);
glEnable(GL_BLEND);
glBlendFunc(GL_SRC_ALPHA,GL_ONE_MINUS_SRC_ALPHA);
if(1==iCoordinateaxis){
glColor3f(1.0f,1.0f,1.0f);
glBegin(GL_LINES);
glVertex3f(-90.0f,00.0f,0.0f);
glVertex3f(90.0f,0.0f,0.0f);
glVertex3f(0.0f,-90.0f,0.0f);
glVertex3f(0.0f,90.0f,0.0f);
glVertex3f(0.0f,0.0f,-90.0f);
glVertex3f(0.0f,0.0f,90.0f);
glEnd();
glPushMatrix();
glTranslatef(90.0f,0.0f,0.0f);
glRotatef(90.0f,0.0f,1.0f,0.0f);
glutSolidCone(3,6,10,10);
glPopMatrix();
glPushMatrix();
glTranslatef(0.0f,90.0f,0.0f);
glRotatef(-90.0f,1.0f,0.0f,0.0f);
glutSolidCone(3,6,10,10);
glPopMatrix();
glPushMatrix();
glTranslatef(0.0f,0.0f,90.0f);
glRotatef(70.0f,0.0f,0.0f,1.0f);
glutSolidCone(3,6,10,10);
glPopMatrix();
}
glColor3f(0.5f,0.5f,1.0f);
memset(transformationMatrix,0,sizeof(transformationMatrix));
//打印变换矩阵
if(2==iPrintMatrix){
printf("--------------------------------------\n");
for(int i=0;i<4;i++){
for(int j=0;j<4;j++){
printf("%9.6f ",transformationMatrix[4*j+i]);
}
printf("\n");
}
}
m3dRotationMatrix44(transformationMatrix, m3dDegToRad(yRot), 0.0f, 1.0f, 0.0f);
//transformationMatrix[12]、transformationMatrix[13] = 0.0f、transformationMatrix[14] = 0.0f是平移参数,分别代表x、y、 z轴的偏移参数。
//transformationMatrix[15]代表缩放为原来的1/transformationMatrix[15]
transformationMatrix[12] = 0.0f;
transformationMatrix[13] = 0.0f;
transformationMatrix[14] = 0.0f;
transformationMatrix[15] = 2.0f;
//打印变换矩阵
if(2==iPrintMatrix){
printf("--------------------------------------\n");
for(int i=0;i<4;i++){
for(int j=0;j<4;j++){
printf("%9.6f ",transformationMatrix[4*j+i]);
}
printf("\n");
}
}
if(1==iCylinder)
DrawCylinder(transformationMatrix);
else
DrawTorus(transformationMatrix);
//恢复压入栈的Matrix
glPopMatrix();
//交换两个缓冲区的指针
glutSwapBuffers();
}
//设置Redering State
void setupRederingState(void){
glEnable(GL_DEPTH_TEST); //使能深度测试
glFrontFace(GL_CCW); //多边形逆时针方向为正面
//glEnable(GL_CULL_FACE); //不显示背面
glPolygonMode(GL_FRONT_AND_BACK,GL_LINE);//背面正面均使用线填充
//设置清理颜色为黑色
glClearColor(0.0f,0.0,0.0,1.0f);
//设置绘画颜色为绿色
glColor3f(1.0f,1.0f,0.0f);
//使能深度测试
glEnable(GL_DEPTH_TEST);
//获取受支持的点大小范围
glGetFloatv(GL_POINT_SIZE_RANGE,sizes);
//获取受支持的点大小增量
glGetFloatv(GL_POINT_SIZE_GRANULARITY,&step);
//获取最大的投影矩阵堆栈深度
glGetIntegerv( GL_MAX_PROJECTION_STACK_DEPTH,&iMaxProjectionStackDepth);
//获取最大的模型视图矩阵堆栈深度
glGetIntegerv( GL_MAX_MODELVIEW_STACK_DEPTH,&iMaxModeviewStackDepth);
//获取最大的纹理矩阵堆栈深度
glGetIntegerv( GL_MAX_TEXTURE_STACK_DEPTH,&iMaxTextureStackDepth);
printf("point size range:%f-%f\n",sizes[0],sizes[1]);
printf("point step:%f\n",step);
printf("iMaxProjectionStackDepth=%d\n",iMaxProjectionStackDepth);
printf("iMaxModeviewStackDepth=%d\n",iMaxModeviewStackDepth);
printf("iMaxTextureStackDepth=%d\n",iMaxTextureStackDepth);
}
//窗口大小变化回调函数
void changSize(GLint w,GLint h){
//横宽比率
GLfloat ratio;
//设置坐标系为x(-100.0f,100.0f)、y(-100.0f,100.0f)、z(-100.0f,100.0f)
GLfloat coordinatesize=100.0f;
//窗口宽高为零直接返回
if((w==0)||(h==0))
return;
//设置视口和窗口大小一致
glViewport(0,0,w,h);
//对投影矩阵应用随后的矩阵操作
glMatrixMode(GL_PROJECTION);
//重置当前指定的矩阵为单位矩阵
glLoadIdentity();
ratio=(GLfloat)w/(GLfloat)h;
//正交投影
if(1==iProjectionMode){
printf("glOrtho\n");
if(w<h)
glOrtho(-coordinatesize,coordinatesize,-coordinatesize/ratio,coordinatesize/ratio,-coordinatesize,coordinatesize);
else
glOrtho(-coordinatesize*ratio,coordinatesize*ratio,-coordinatesize,coordinatesize,-coordinatesize,coordinatesize);
//当前矩阵设置为模型视图矩阵
glMatrixMode(GL_MODELVIEW);
//重置当前指定的矩阵为单位矩阵
glLoadIdentity();
}
else{
printf("gluPerspective\n");
gluPerspective(45,ratio,10.0f,500.0f);
//当前矩阵设置为模型视图矩阵
glMatrixMode(GL_MODELVIEW);
//重置当前指定的矩阵为单位矩阵
glLoadIdentity();
}
}
//按键输入处理回调函数
void specialKey(int key,int x,int y){
if(key==GLUT_KEY_UP){
xRotAngle-=5.0f;
}
else if(key==GLUT_KEY_DOWN){
xRotAngle+=5.0f;
}
else if(key==GLUT_KEY_LEFT){
yRotAngle-=5.0f;
}
else if(key==GLUT_KEY_RIGHT){
yRotAngle+=5.0f;
}
//重新绘制
glutPostRedisplay();
}
void timerFunc(int value)
{
glutPostRedisplay();
glutTimerFunc(10, timerFunc, 1);
}
int main(int argc, char* argv[])
{
//菜单
GLint iMainMenu;
GLint iCoordinateaxisMenu;
GLint iOrthoOrPerspectMenu;
GLint iPrintmatrix;
GLint iCylinderOrTorus;
//初始化glut
glutInit(&argc,argv);
//使用双缓冲区、深度缓冲区。
glutInitDisplayMode(GLUT_DOUBLE|GLUT_RGBA|GLUT_DEPTH);
//获取系统的宽像素
SCREEN_WIDTH=glutGet(GLUT_SCREEN_WIDTH);
//获取系统的高像素
SCREEN_HEIGHT=glutGet(GLUT_SCREEN_HEIGHT);
//创建窗口,窗口名字为OpenGL Transform Demo
glutCreateWindow("OpenGL Transform Demo");
//设置窗口大小
glutReshapeWindow(windowWidth,windowHeight);
//窗口居中显示
glutPositionWindow((SCREEN_WIDTH-windowWidth)/2,(SCREEN_HEIGHT-windowHeight)/2);
//窗口大小变化时的处理函数
glutReshapeFunc(changSize);
//设置显示回调函数
glutDisplayFunc(renderScreen);
//设置按键输入处理回调函数
glutSpecialFunc(specialKey);
//菜单回调函数
iCoordinateaxisMenu=glutCreateMenu(processMenu);
//添加菜单
glutAddMenuEntry("Display coordinate axis",1);
glutAddMenuEntry("Don't dispaly coordinate axis",2);
iOrthoOrPerspectMenu=glutCreateMenu(processMenu);
glutAddMenuEntry("Ortho",3);
glutAddMenuEntry("Perspect",4);
iPrintmatrix=glutCreateMenu(processMenu);
glutAddMenuEntry("Don't print Matrix",5);
glutAddMenuEntry("Print Matrix",6);
iCylinderOrTorus=glutCreateMenu(processMenu);
glutAddMenuEntry("Cylinder",7);
glutAddMenuEntry("Torus",8);
iMainMenu=glutCreateMenu(processMenu);
glutAddSubMenu("Whether Display coordinate axis",iCoordinateaxisMenu);
glutAddSubMenu("Ortho Or Perspect",iOrthoOrPerspectMenu);
glutAddSubMenu("Whether Print Matrix",iPrintmatrix);
glutAddSubMenu("Cylinder or torus",iCylinderOrTorus);
//将菜单榜定到鼠标右键上
glutAttachMenu(GLUT_RIGHT_BUTTON);
glutTimerFunc(10,timerFunc, 1);
//设置全局渲染参数
setupRederingState();
glutMainLoop();
return 0;
}
math3d.h
// Math3d.h
// Header file for the Math3d library. The C-Runtime has math.h, this file and the
// accompanying math.c are meant to suppliment math.h by adding geometry/math routines
// useful for graphics, simulation, and physics applications (3D stuff).
// Richard S. Wright Jr.
#ifndef _MATH3D_LIBRARY__
#define _MATH3D_LIBRARY__
#include <math.h>
#include <memory.h>
///////////////////////////////////////////////////////////////////////////////
// Data structures and containers
// Much thought went into how these are declared. Many libraries declare these
// as structures with x, y, z data members. However structure alignment issues
// could limit the portability of code based on such structures, or the binary
// compatibility of data files (more likely) that contain such structures across
// compilers/platforms. Arrays are always tightly packed, and are more efficient
// for moving blocks of data around (usually).
typedef float M3DVector3f[3]; // Vector of three floats (x, y, z)
typedef double M3DVector3d[3]; // Vector of three doubles (x, y, z)
typedef float M3DVector4f[4]; // Lesser used... Do we really need these?
typedef double M3DVector4d[4]; // Yes, occasionaly
typedef float M3DVector2f[2]; // 3D points = 3D Vectors, but we need a
typedef double M3DVector2d[2]; // 2D representations sometimes... (x,y) order
// 3x3 matrix - column major. X vector is 0, 1, 2, etc.
// 0 3 6
// 1 4 7
// 2 5 8
typedef float M3DMatrix33f[9]; // A 3 x 3 matrix, column major (floats) - OpenGL Style
typedef double M3DMatrix33d[9]; // A 3 x 3 matrix, column major (doubles) - OpenGL Style
// 4x4 matrix - column major. X vector is 0, 1, 2, etc.
// 0 4 8 12
// 1 5 9 13
// 2 6 10 14
// 3 7 11 15
typedef float M3DMatrix44f[16]; // A 4 X 4 matrix, column major (floats) - OpenGL style
typedef double M3DMatrix44d[16]; // A 4 x 4 matrix, column major (doubles) - OpenGL style
///////////////////////////////////////////////////////////////////////////////
// Useful constants
#define M3D_PI (3.14159265358979323846)
#define M3D_2PI (2.0 * M3D_PI)
#define M3D_PI_DIV_180 (0.017453292519943296)
#define M3D_INV_PI_DIV_180 (57.2957795130823229)
///////////////////////////////////////////////////////////////////////////////
// Useful shortcuts and macros
// Radians are king... but we need a way to swap back and forth
#define m3dDegToRad(x) ((x)*M3D_PI_DIV_180)
#define m3dRadToDeg(x) ((x)*M3D_INV_PI_DIV_180)
// Hour angles
#define m3dHrToDeg(x) ((x) * (1.0 / 15.0))
#define m3dHrToRad(x) m3dDegToRad(m3dHrToDeg(x))
#define m3dDegToHr(x) ((x) * 15.0))
#define m3dRadToHr(x) m3dDegToHr(m3dRadToDeg(x))
// Returns the same number if it is a power of
// two. Returns a larger integer if it is not a
// power of two. The larger integer is the next
// highest power of two.
inline unsigned int m3dIsPOW2(unsigned int iValue)
{
unsigned int nPow2 = 1;
while(iValue > nPow2)
nPow2 = (nPow2 << 1);
return nPow2;
}
///////////////////////////////////////////////////////////////////////////////
// Inline accessor functions for people who just can't count to 3 - Vectors
#define m3dGetVectorX(v) (v[0])
#define m3dGetVectorY(v) (v[1])
#define m3dGetVectorZ(v) (v[2])
#define m3dGetVectorW(v) (v[3])
#define m3dSetVectorX(v, x) ((v)[0] = (x))
#define m3dSetVectorY(v, y) ((v)[1] = (y))
#define m3dSetVectorZ(v, z) ((v)[2] = (z))
#define m3dSetVectorW(v, w) ((v)[3] = (w))
///////////////////////////////////////////////////////////////////////////////
// Inline vector functions
// Load Vector with (x, y, z, w).
inline void m3dLoadVector2(M3DVector2f v, float x, float y)
{ v[0] = x; v[1] = y; }
inline void m3dLoadVector2(M3DVector2d v, float x, float y)
{ v[0] = x; v[1] = y; }
inline void m3dLoadVector3(M3DVector3f v, float x, float y, float z)
{ v[0] = x; v[1] = y; v[2] = z; }
inline void m3dLoadVector3(M3DVector3d v, double x, double y, double z)
{ v[0] = x; v[1] = y; v[2] = z; }
inline void m3dLoadVector4(M3DVector4f v, float x, float y, float z, float w)
{ v[0] = x; v[1] = y; v[2] = z; v[3] = w;}
inline void m3dLoadVector4(M3DVector4d v, double x, double y, double z, double w)
{ v[0] = x; v[1] = y; v[2] = z; v[3] = w;}
////////////////////////////////////////////////////////////////////////////////
// Copy vector src into vector dst
inline void m3dCopyVector2(M3DVector2f dst, const M3DVector2f src) { memcpy(dst, src, sizeof(M3DVector2f)); }
inline void m3dCopyVector2(M3DVector2d dst, const M3DVector2d src) { memcpy(dst, src, sizeof(M3DVector2d)); }
inline void m3dCopyVector3(M3DVector3f dst, const M3DVector3f src) { memcpy(dst, src, sizeof(M3DVector3f)); }
inline void m3dCopyVector3(M3DVector3d dst, const M3DVector3d src) { memcpy(dst, src, sizeof(M3DVector3d)); }
inline void m3dCopyVector4(M3DVector4f dst, const M3DVector4f src) { memcpy(dst, src, sizeof(M3DVector4f)); }
inline void m3dCopyVector4(M3DVector4d dst, const M3DVector4d src) { memcpy(dst, src, sizeof(M3DVector4d)); }
////////////////////////////////////////////////////////////////////////////////
// Add Vectors (r, a, b) r = a + b
inline void m3dAddVectors2(M3DVector2f r, const M3DVector2f a, const M3DVector2f b)
{ r[0] = a[0] + b[0]; r[1] = a[1] + b[1]; }
inline void m3dAddVectors2(M3DVector2d r, const M3DVector2d a, const M3DVector2d b)
{ r[0] = a[0] + b[0]; r[1] = a[1] + b[1]; }
inline void m3dAddVectors3(M3DVector3f r, const M3DVector3f a, const M3DVector3f b)
{ r[0] = a[0] + b[0]; r[1] = a[1] + b[1]; r[2] = a[2] + b[2]; }
inline void m3dAddVectors3(M3DVector3d r, const M3DVector3d a, const M3DVector3d b)
{ r[0] = a[0] + b[0]; r[1] = a[1] + b[1]; r[2] = a[2] + b[2]; }
inline void m3dAddVectors4(M3DVector4f r, const M3DVector4f a, const M3DVector4f b)
{ r[0] = a[0] + b[0]; r[1] = a[1] + b[1]; r[2] = a[2] + b[2]; r[3] = a[3] + b[3]; }
inline void m3dAddVectors4(M3DVector4d r, const M3DVector4d a, const M3DVector4d b)
{ r[0] = a[0] + b[0]; r[1] = a[1] + b[1]; r[2] = a[2] + b[2]; r[3] = a[3] + b[3]; }
////////////////////////////////////////////////////////////////////////////////
// Subtract Vectors (r, a, b) r = a - b
inline void m3dSubtractVectors2(M3DVector2f r, const M3DVector2f a, const M3DVector2f b)
{ r[0] = a[0] - b[0]; r[1] = a[1] - b[1]; }
inline void m3dSubtractVectors2(M3DVector2d r, const M3DVector2d a, const M3DVector2d b)
{ r[0] = a[0] - b[0]; r[1] = a[1] - b[1]; }
inline void m3dSubtractVectors3(M3DVector3f r, const M3DVector3f a, const M3DVector3f b)
{ r[0] = a[0] - b[0]; r[1] = a[1] - b[1]; r[2] = a[2] - b[2]; }
inline void m3dSubtractVectors3(M3DVector3d r, const M3DVector3d a, const M3DVector3d b)
{ r[0] = a[0] - b[0]; r[1] = a[1] - b[1]; r[2] = a[2] - b[2]; }
inline void m3dSubtractVectors4(M3DVector4f r, const M3DVector4f a, const M3DVector4f b)
{ r[0] = a[0] - b[0]; r[1] = a[1] - b[1]; r[2] = a[2] - b[2]; r[3] = a[3] - b[3]; }
inline void m3dSubtractVectors4(M3DVector4d r, const M3DVector4d a, const M3DVector4d b)
{ r[0] = a[0] - b[0]; r[1] = a[1] - b[1]; r[2] = a[2] - b[2]; r[3] = a[3] - b[3]; }
///////////////////////////////////////////////////////////////////////////////////////
// Scale Vectors (in place)
inline void m3dScaleVector2(M3DVector2f v, float scale)
{ v[0] *= scale; v[1] *= scale; }
inline void m3dScaleVector2(M3DVector2d v, double scale)
{ v[0] *= scale; v[1] *= scale; }
inline void m3dScaleVector3(M3DVector3f v, float scale)
{ v[0] *= scale; v[1] *= scale; v[2] *= scale; }
inline void m3dScaleVector3(M3DVector3d v, double scale)
{ v[0] *= scale; v[1] *= scale; v[2] *= scale; }
inline void m3dScaleVector4(M3DVector4f v, float scale)
{ v[0] *= scale; v[1] *= scale; v[2] *= scale; v[3] *= scale; }
inline void m3dScaleVector4(M3DVector4d v, double scale)
{ v[0] *= scale; v[1] *= scale; v[2] *= scale; v[3] *= scale; }
//////////////////////////////////////////////////////////////////////////////////////
// Cross Product
// u x v = result
// We only need one version for floats, and one version for doubles. A 3 component
// vector fits in a 4 component vector. If M3DVector4d or M3DVector4f are passed
// we will be OK because 4th component is not used.
inline void m3dCrossProduct(M3DVector3f result, const M3DVector3f u, const M3DVector3f v)
{
result[0] = u[1]*v[2] - v[1]*u[2];
result[1] = -u[0]*v[2] + v[0]*u[2];
result[2] = u[0]*v[1] - v[0]*u[1];
}
inline void m3dCrossProduct(M3DVector3d result, const M3DVector3d u, const M3DVector3d v)
{
result[0] = u[1]*v[2] - v[1]*u[2];
result[1] = -u[0]*v[2] + v[0]*u[2];
result[2] = u[0]*v[1] - v[0]*u[1];
}
//////////////////////////////////////////////////////////////////////////////////////
// Dot Product, only for three component vectors
// return u dot v
inline float m3dDotProduct(const M3DVector3f u, const M3DVector3f v)
{ return u[0]*v[0] + u[1]*v[1] + u[2]*v[2]; }
inline double m3dDotProduct(const M3DVector3d u, const M3DVector3d v)
{ return u[0]*v[0] + u[1]*v[1] + u[2]*v[2]; }
//////////////////////////////////////////////////////////////////////////////////////
// Angle between vectors, only for three component vectors. Angle is in radians...
inline float m3dGetAngleBetweenVectors(const M3DVector3f u, const M3DVector3f v)
{
float dTemp = m3dDotProduct(u, v);
return float(acos(double(dTemp)));
}
inline double m3dGetAngleBetweenVectors(const M3DVector3d u, const M3DVector3d v)
{
double dTemp = m3dDotProduct(u, v);
return acos(dTemp);
}
//////////////////////////////////////////////////////////////////////////////////////
// Get Square of a vectors length
// Only for three component vectors
inline float m3dGetVectorLengthSquared(const M3DVector3f u)
{ return (u[0] * u[0]) + (u[1] * u[1]) + (u[2] * u[2]); }
inline double m3dGetVectorLengthSquared(const M3DVector3d u)
{ return (u[0] * u[0]) + (u[1] * u[1]) + (u[2] * u[2]); }
//////////////////////////////////////////////////////////////////////////////////////
// Get lenght of vector
// Only for three component vectors.
inline float m3dGetVectorLength(const M3DVector3f u)
{ return float(sqrt(double(m3dGetVectorLengthSquared(u)))); }
inline double m3dGetVectorLength(const M3DVector3d u)
{ return sqrt(m3dGetVectorLengthSquared(u)); }
//////////////////////////////////////////////////////////////////////////////////////
// Normalize a vector
// Scale a vector to unit length. Easy, just scale the vector by it's length
inline void m3dNormalizeVector(M3DVector3f u)
{ m3dScaleVector3(u, 1.0f / m3dGetVectorLength(u)); }
inline void m3dNormalizeVector(M3DVector3d u)
{ m3dScaleVector3(u, 1.0 / m3dGetVectorLength(u)); }
//////////////////////////////////////////////////////////////////////////////////////
// Get the distance between two points. The distance between two points is just
// the magnitude of the difference between two vectors
// Located in math.cpp
float m3dGetDistanceSquared(const M3DVector3f u, const M3DVector3f v);
double m3dGetDistanceSquared(const M3DVector3d u, const M3DVector3d v);
inline double m3dGetDistance(const M3DVector3d u, const M3DVector3d v)
{ return sqrt(m3dGetDistanceSquared(u, v)); }
inline float m3dGetDistance(const M3DVector3f u, const M3DVector3f v)
{ return float(sqrt(m3dGetDistanceSquared(u, v))); }
inline float m3dGetMagnitudeSquared(const M3DVector3f u) { return u[0]*u[0] + u[1]*u[1] + u[2]*u[2]; }
inline double m3dGetMagnitudeSquared(const M3DVector3d u) { return u[0]*u[0] + u[1]*u[1] + u[2]*u[2]; }
inline float m3dGetMagnitude(const M3DVector3f u) { return float(sqrt(m3dGetMagnitudeSquared(u))); }
inline double m3dGetMagnitude(const M3DVector3d u) { return sqrt(m3dGetMagnitudeSquared(u)); }
//////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Matrix functions
// Both floating point and double precision 3x3 and 4x4 matricies are supported.
// No support is included for arbitrarily dimensioned matricies on purpose, since
// the 3x3 and 4x4 matrix routines are the most common for the purposes of this
// library. Matrices are column major, like OpenGL matrices.
// Unlike the vector functions, some of these are going to have to not be inlined,
// although many will be.
// Copy Matrix
// Brain-dead memcpy
inline void m3dCopyMatrix33(M3DMatrix33f dst, const M3DMatrix33f src)
{ memcpy(dst, src, sizeof(M3DMatrix33f)); }
inline void m3dCopyMatrix33(M3DMatrix33d dst, const M3DMatrix33d src)
{ memcpy(dst, src, sizeof(M3DMatrix33d)); }
inline void m3dCopyMatrix44(M3DMatrix44f dst, const M3DMatrix44f src)
{ memcpy(dst, src, sizeof(M3DMatrix44f)); }
inline void m3dCopyMatrix44(M3DMatrix44d dst, const M3DMatrix44d src)
{ memcpy(dst, src, sizeof(M3DMatrix44d)); }
// LoadIdentity
// Implemented in Math3d.cpp
void m3dLoadIdentity33(M3DMatrix33f m);
void m3dLoadIdentity33(M3DMatrix33d m);
void m3dLoadIdentity44(M3DMatrix44f m);
void m3dLoadIdentity44(M3DMatrix44d m);
/////////////////////////////////////////////////////////////////////////////
// Get/Set Column.
inline void m3dGetMatrixColumn33(M3DVector3f dst, const M3DMatrix33f src, int column)
{ memcpy(dst, src + (3 * column), sizeof(float) * 3); }
inline void m3dGetMatrixColumn33(M3DVector3d dst, const M3DMatrix33d src, int column)
{ memcpy(dst, src + (3 * column), sizeof(double) * 3); }
inline void m3dSetMatrixColumn33(M3DMatrix33f dst, const M3DVector3f src, int column)
{ memcpy(dst + (3 * column), src, sizeof(float) * 3); }
inline void m3dSetMatrixColumn33(M3DMatrix33d dst, const M3DVector3d src, int column)
{ memcpy(dst + (3 * column), src, sizeof(double) * 3); }
inline void m3dGetMatrixColumn44(M3DVector4f dst, const M3DMatrix44f src, int column)
{ memcpy(dst, src + (4 * column), sizeof(float) * 4); }
inline void m3dGetMatrixColumn44(M3DVector4d dst, const M3DMatrix44d src, int column)
{ memcpy(dst, src + (4 * column), sizeof(double) * 4); }
inline void m3dSetMatrixColumn44(M3DMatrix44f dst, const M3DVector4f src, int column)
{ memcpy(dst + (4 * column), src, sizeof(float) * 4); }
inline void m3dSetMatrixColumn44(M3DMatrix44d dst, const M3DVector4d src, int column)
{ memcpy(dst + (4 * column), src, sizeof(double) * 4); }
// Get/Set row purposely omitted... use the functions below.
// I don't think row vectors are useful for column major ordering...
// If I'm wrong, add them later.
//////////////////////////////////////////////////////////////////////////////
// Get/Set RowCol - Remember column major ordering...
// Provides for element addressing
inline void m3dSetMatrixRowCol33(M3DMatrix33f m, int row, int col, float value)
{ m[(col * 3) + row] = value; }
inline float m3dGetMatrixRowCol33(const M3DMatrix33f m, int row, int col)
{ return m[(col * 3) + row]; }
inline void m3dSetMatrixRowCol33(M3DMatrix33d m, int row, int col, double value)
{ m[(col * 3) + row] = value; }
inline double m3dGetMatrixRowCol33(const M3DMatrix33d m, int row, int col)
{ return m[(col * 3) + row]; }
inline void m3dSetMatrixRowCol44(M3DMatrix44f m, int row, int col, float value)
{ m[(col * 4) + row] = value; }
inline float m3dGetMatrixRowCol44(const M3DMatrix44f m, int row, int col)
{ return m[(col * 4) + row]; }
inline void m3dSetMatrixRowCol44(M3DMatrix44d m, int row, int col, double value)
{ m[(col * 4) + row] = value; }
inline double m3dGetMatrixRowCol44(const M3DMatrix44d m, int row, int col)
{ return m[(col * 4) + row]; }
///////////////////////////////////////////////////////////////////////////////
// Extract a rotation matrix from a 4x4 matrix
// Extracts the rotation matrix (3x3) from a 4x4 matrix
inline void m3dExtractRotation(M3DMatrix33f dst, const M3DMatrix44f src)
{
memcpy(dst, src, sizeof(float) * 3); // X column
memcpy(dst + 3, src + 4, sizeof(float) * 3); // Y column
memcpy(dst + 6, src + 8, sizeof(float) * 3); // Z column
}
// Ditto above, but for doubles
inline void m3dExtractRotation(M3DMatrix33d dst, const M3DMatrix44d src)
{
memcpy(dst, src, sizeof(double) * 3); // X column
memcpy(dst + 3, src + 4, sizeof(double) * 3); // Y column
memcpy(dst + 6, src + 8, sizeof(double) * 3); // Z column
}
// Inject Rotation (3x3) into a full 4x4 matrix...
inline void m3dInjectRotation(M3DMatrix44f dst, const M3DMatrix33f src)
{
memcpy(dst, src, sizeof(float) * 4);
memcpy(dst + 4, src + 4, sizeof(float) * 4);
memcpy(dst + 8, src + 8, sizeof(float) * 4);
}
// Ditto above for doubles
inline void m3dInjectRotation(M3DMatrix44d dst, const M3DMatrix33d src)
{
memcpy(dst, src, sizeof(double) * 4);
memcpy(dst + 4, src + 4, sizeof(double) * 4);
memcpy(dst + 8, src + 8, sizeof(double) * 4);
}
////////////////////////////////////////////////////////////////////////////////
// MultMatrix
// Implemented in Math.cpp
void m3dMatrixMultiply44(M3DMatrix44f product, const M3DMatrix44f a, const M3DMatrix44f b);
void m3dMatrixMultiply44(M3DMatrix44d product, const M3DMatrix44d a, const M3DMatrix44d b);
void m3dMatrixMultiply33(M3DMatrix33f product, const M3DMatrix33f a, const M3DMatrix33f b);
void m3dMatrixMultiply33(M3DMatrix33d product, const M3DMatrix33d a, const M3DMatrix33d b);
// Transform - Does rotation and translation via a 4x4 matrix. Transforms
// a point or vector.
// By-the-way __inline means I'm asking the compiler to do a cost/benefit analysis. If
// these are used frequently, they may not be inlined to save memory. I'm experimenting
// with this....
__inline void m3dTransformVector3(M3DVector3f vOut, const M3DVector3f v, const M3DMatrix44f m)
{
vOut[0] = m[0] * v[0] + m[4] * v[1] + m[8] * v[2] + m[12];// * v[3];
vOut[1] = m[1] * v[0] + m[5] * v[1] + m[9] * v[2] + m[13];// * v[3];
vOut[2] = m[2] * v[0] + m[6] * v[1] + m[10] * v[2] + m[14];// * v[3];
//vOut[3] = m[3] * v[0] + m[7] * v[1] + m[11] * v[2] + m[15] * v[3];
}
// Ditto above, but for doubles
__inline void m3dTransformVector3(M3DVector3d vOut, const M3DVector3d v, const M3DMatrix44d m)
{
vOut[0] = m[0] * v[0] + m[4] * v[1] + m[8] * v[2] + m[12];// * v[3];
vOut[1] = m[1] * v[0] + m[5] * v[1] + m[9] * v[2] + m[13];// * v[3];
vOut[2] = m[2] * v[0] + m[6] * v[1] + m[10] * v[2] + m[14];// * v[3];
//vOut[3] = m[3] * v[0] + m[7] * v[1] + m[11] * v[2] + m[15] * v[3];
}
__inline void m3dTransformVector4(M3DVector4f vOut, const M3DVector4f v, const M3DMatrix44f m)
{
vOut[0] = m[0] * v[0] + m[4] * v[1] + m[8] * v[2] + m[12] * v[3];
vOut[1] = m[1] * v[0] + m[5] * v[1] + m[9] * v[2] + m[13] * v[3];
vOut[2] = m[2] * v[0] + m[6] * v[1] + m[10] * v[2] + m[14] * v[3];
vOut[3] = m[3] * v[0] + m[7] * v[1] + m[11] * v[2] + m[15] * v[3];
}
// Ditto above, but for doubles
__inline void m3dTransformVector4(M3DVector4d vOut, const M3DVector4d v, const M3DMatrix44d m)
{
vOut[0] = m[0] * v[0] + m[4] * v[1] + m[8] * v[2] + m[12] * v[3];
vOut[1] = m[1] * v[0] + m[5] * v[1] + m[9] * v[2] + m[13] * v[3];
vOut[2] = m[2] * v[0] + m[6] * v[1] + m[10] * v[2] + m[14] * v[3];
vOut[3] = m[3] * v[0] + m[7] * v[1] + m[11] * v[2] + m[15] * v[3];
}
// Just do the rotation, not the translation... this is usually done with a 3x3
// Matrix.
__inline void m3dRotateVector(M3DVector3f vOut, const M3DVector3f p, const M3DMatrix33f m)
{
vOut[0] = m[0] * p[0] + m[3] * p[1] + m[6] * p[2];
vOut[1] = m[1] * p[0] + m[4] * p[1] + m[7] * p[2];
vOut[2] = m[2] * p[0] + m[5] * p[1] + m[8] * p[2];
}
// Ditto above, but for doubles
__inline void m3dRotateVector(M3DVector3d vOut, const M3DVector3d p, const M3DMatrix33d m)
{
vOut[0] = m[0] * p[0] + m[3] * p[1] + m[6] * p[2];
vOut[1] = m[1] * p[0] + m[4] * p[1] + m[7] * p[2];
vOut[2] = m[2] * p[0] + m[5] * p[1] + m[8] * p[2];
}
// Scale a matrix (I don't beleive in Scaling matricies ;-)
// Yes, it's faster to loop backwards... These could be
// unrolled... but eh... if you find this is a bottleneck,
// then you should unroll it yourself
inline void m3dScaleMatrix33(M3DMatrix33f m, float scale)
{ for(int i = 8; i >=0; i--) m[i] *= scale; }
inline void m3dScaleMatrix33(M3DMatrix33d m, double scale)
{ for(int i = 8; i >=0; i--) m[i] *= scale; }
inline void m3dScaleMatrix44(M3DMatrix44f m, float scale)
{ for(int i = 15; i >=0; i--) m[i] *= scale; }
inline void m3dScaleMatrix44(M3DMatrix44d m, double scale)
{ for(int i = 15; i >=0; i--) m[i] *= scale; }
// Create a Rotation matrix
// Implemented in math.cpp
void m3dRotationMatrix33(M3DMatrix33f m, float angle, float x, float y, float z);
void m3dRotationMatrix33(M3DMatrix33d m, double angle, double x, double y, double z);
void m3dRotationMatrix44(M3DMatrix44f m, float angle, float x, float y, float z);
void m3dRotationMatrix44(M3DMatrix44d m, double angle, double x, double y, double z);
// Create a Translation matrix. Only 4x4 matrices have translation components
inline void m3dTranslationMatrix44(M3DMatrix44f m, float x, float y, float z)
{ m3dLoadIdentity44(m); m[12] = x; m[13] = y; m[14] = z; }
inline void m3dTranslationMatrix44(M3DMatrix44d m, double x, double y, double z)
{ m3dLoadIdentity44(m); m[12] = x; m[13] = y; m[14] = z; }
// Translate matrix. Only 4x4 matrices supported
inline void m3dTranslateMatrix44(M3DMatrix44f m, float x, float y, float z)
{ m[12] += x; m[13] += y; m[14] += z; }
inline void m3dTranslateMatrix44(M3DMatrix44d m, double x, double y, double z)
{ m[12] += x; m[13] += y; m[14] += z; }
// Scale matrix. Only 4x4 matrices supported
inline void m3dScaleMatrix44(M3DMatrix44f m, float x, float y, float z)
{ m[0] *= x; m[5] *= y; m[10] *= z; }
inline void m3dScaleMatrix44(M3DMatrix44d m, double x, double y, double z)
{ m[0] *= x; m[5] *= y; m[10] *= z; }
// Transpose/Invert - Only 4x4 matricies supported
#define TRANSPOSE44(dst, src) \
{ \
for (int j = 0; j < 4; j++) \
{ \
for (int i = 0; i < 4; i++) \
{ \
dst[(j*4)+i] = src[(i*4)+j]; \
} \
} \
}
inline void m3dTransposeMatrix44(M3DMatrix44f dst, const M3DMatrix44f src)
{ TRANSPOSE44(dst, src); }
inline void m3dTransposeMatrix44(M3DMatrix44d dst, const M3DMatrix44d src)
{ TRANSPOSE44(dst, src); }
bool m3dInvertMatrix44(M3DMatrix44f dst, const M3DMatrix44f src);
bool m3dInvertMatrix44(M3DMatrix44d dst, const M3DMatrix44d src);
///////////////////////////////////////////////////////////////////////////////
///////////////////////////////////////////////////////////////////////////////
///////////////////////////////////////////////////////////////////////////////
// Other Miscellaneous functions
// Find a normal from three points
// Implemented in math3d.cpp
void m3dFindNormal(M3DVector3f result, const M3DVector3f point1, const M3DVector3f point2,
const M3DVector3f point3);
void m3dFindNormal(M3DVector3d result, const M3DVector3d point1, const M3DVector3d point2,
const M3DVector3d point3);
// Calculates the signed distance of a point to a plane
inline float m3dGetDistanceToPlane(const M3DVector3f point, const M3DVector4f plane)
{ return point[0]*plane[0] + point[1]*plane[1] + point[2]*plane[2] + plane[3]; }
inline double m3dGetDistanceToPlane(const M3DVector3d point, const M3DVector4d plane)
{ return point[0]*plane[0] + point[1]*plane[1] + point[2]*plane[2] + plane[3]; }
// Get plane equation from three points and a normal
void m3dGetPlaneEquation(M3DVector4f planeEq, const M3DVector3f p1, const M3DVector3f p2, const M3DVector3f p3);
void m3dGetPlaneEquation(M3DVector4d planeEq, const M3DVector3d p1, const M3DVector3d p2, const M3DVector3d p3);
// Determine if a ray intersects a sphere
double m3dRaySphereTest(const M3DVector3d point, const M3DVector3d ray, const M3DVector3d sphereCenter, double sphereRadius);
float m3dRaySphereTest(const M3DVector3f point, const M3DVector3f ray, const M3DVector3f sphereCenter, float sphereRadius);
// Etc. etc.
///////////////////////////////////////////////////////////////////////////////////////////////////////
// Faster (and more robust) replacements for gluProject
void m3dProjectXY( M3DVector2f vPointOut, const M3DMatrix44f mModelView, const M3DMatrix44f mProjection, const int iViewPort[4], const M3DVector3f vPointIn);
void m3dProjectXYZ(M3DVector3f vPointOut, const M3DMatrix44f mModelView, const M3DMatrix44f mProjection, const int iViewPort[4], const M3DVector3f vPointIn);
//////////////////////////////////////////////////////////////////////////////////////////////////
// This function does a three dimensional Catmull-Rom "spline" interpolation between p1 and p2
void m3dCatmullRom(M3DVector3f vOut, M3DVector3f vP0, M3DVector3f vP1, M3DVector3f vP2, M3DVector3f vP3, float t);
void m3dCatmullRom(M3DVector3d vOut, M3DVector3d vP0, M3DVector3d vP1, M3DVector3d vP2, M3DVector3d vP3, double t);
//////////////////////////////////////////////////////////////////////////////////////////////////
// Compare floats and doubles...
inline bool m3dCloseEnough(float fCandidate, float fCompare, float fEpsilon)
{
return (fabs(fCandidate - fCompare) < fEpsilon);
}
inline bool m3dCloseEnough(double dCandidate, double dCompare, double dEpsilon)
{
return (fabs(dCandidate - dCompare) < dEpsilon);
}
////////////////////////////////////////////////////////////////////////////
// Used for normal mapping. Finds the tangent bases for a triangle...
// Only a floating point implementation is provided.
void m3dCalculateTangentBasis(const M3DVector3f pvTriangle[3], const M3DVector2f pvTexCoords[3], const M3DVector3f N, M3DVector3f vTangent);
////////////////////////////////////////////////////////////////////////////
// Smoothly step between 0 and 1 between edge1 and edge 2
double m3dSmoothStep(double edge1, double edge2, double x);
float m3dSmoothStep(float edge1, float edge2, float x);
/////////////////////////////////////////////////////////////////////////////
// Planar shadow Matrix
void m3dMakePlanarShadowMatrix(M3DMatrix44d proj, const M3DVector4d planeEq, const M3DVector3d vLightPos);
void m3dMakePlanarShadowMatrix(M3DMatrix44f proj, const M3DVector4f planeEq, const M3DVector3f vLightPos);
double m3dClosestPointOnRay(M3DVector3d vPointOnRay, const M3DVector3d vRayOrigin, const M3DVector3d vUnitRayDir,
const M3DVector3d vPointInSpace);
float m3dClosestPointOnRay(M3DVector3f vPointOnRay, const M3DVector3f vRayOrigin, const M3DVector3f vUnitRayDir,
const M3DVector3f vPointInSpace);
#endif
Math3d.cpp
// Math3d.c
// Implementation of non-inlined functions in the Math3D Library
// Richard S. Wright Jr.
// These are pretty portable
#include "stdafx.h"
#include <math.h>
#include "math3d.h"
////////////////////////////////////////////////////////////
// LoadIdentity
// For 3x3 and 4x4 float and double matricies.
// 3x3 float
void m3dLoadIdentity33(M3DMatrix33f m)
{
// Don't be fooled, this is still column major
static M3DMatrix33f identity = { 1.0f, 0.0f, 0.0f ,
0.0f, 1.0f, 0.0f,
0.0f, 0.0f, 1.0f };
memcpy(m, identity, sizeof(M3DMatrix33f));
}
// 3x3 double
void m3dLoadIdentity33(M3DMatrix33d m)
{
// Don't be fooled, this is still column major
static M3DMatrix33d identity = { 1.0, 0.0, 0.0 ,
0.0, 1.0, 0.0,
0.0, 0.0, 1.0 };
memcpy(m, identity, sizeof(M3DMatrix33d));
}
// 4x4 float
void m3dLoadIdentity44(M3DMatrix44f m)
{
// Don't be fooled, this is still column major
static M3DMatrix44f identity = { 1.0f, 0.0f, 0.0f, 0.0f,
0.0f, 1.0f, 0.0f, 0.0f,
0.0f, 0.0f, 1.0f, 0.0f,
0.0f, 0.0f, 0.0f, 1.0f };
memcpy(m, identity, sizeof(M3DMatrix44f));
}
// 4x4 double
void m3dLoadIdentity44(M3DMatrix44d m)
{
static M3DMatrix44d identity = { 1.0, 0.0, 0.0, 0.0,
0.0, 1.0, 0.0, 0.0,
0.0, 0.0, 1.0, 0.0,
0.0, 0.0, 0.0, 1.0 };
memcpy(m, identity, sizeof(M3DMatrix44d));
}
////////////////////////////////////////////////////////////////////////
// Return the square of the distance between two points
// Should these be inlined...?
float m3dGetDistanceSquared(const M3DVector3f u, const M3DVector3f v)
{
float x = u[0] - v[0];
x = x*x;
float y = u[1] - v[1];
y = y*y;
float z = u[2] - v[2];
z = z*z;
return (x + y + z);
}
// Ditto above, but for doubles
double m3dGetDistanceSquared(const M3DVector3d u, const M3DVector3d v)
{
double x = u[0] - v[0];
x = x*x;
double y = u[1] - v[1];
y = y*y;
double z = u[2] - v[2];
z = z*z;
return (x + y + z);
}
#define A(row,col) a[(col<<2)+row]
#define B(row,col) b[(col<<2)+row]
#define P(row,col) product[(col<<2)+row]
///////////////////////////////////////////////////////////////////////////////
// Multiply two 4x4 matricies
void m3dMatrixMultiply44(M3DMatrix44f product, const M3DMatrix44f a, const M3DMatrix44f b )
{
for (int i = 0; i < 4; i++) {
float ai0=A(i,0), ai1=A(i,1), ai2=A(i,2), ai3=A(i,3);
P(i,0) = ai0 * B(0,0) + ai1 * B(1,0) + ai2 * B(2,0) + ai3 * B(3,0);
P(i,1) = ai0 * B(0,1) + ai1 * B(1,1) + ai2 * B(2,1) + ai3 * B(3,1);
P(i,2) = ai0 * B(0,2) + ai1 * B(1,2) + ai2 * B(2,2) + ai3 * B(3,2);
P(i,3) = ai0 * B(0,3) + ai1 * B(1,3) + ai2 * B(2,3) + ai3 * B(3,3);
}
}
// Ditto above, but for doubles
void m3dMatrixMultiply(M3DMatrix44d product, const M3DMatrix44d a, const M3DMatrix44d b )
{
for (int i = 0; i < 4; i++) {
double ai0=A(i,0), ai1=A(i,1), ai2=A(i,2), ai3=A(i,3);
P(i,0) = ai0 * B(0,0) + ai1 * B(1,0) + ai2 * B(2,0) + ai3 * B(3,0);
P(i,1) = ai0 * B(0,1) + ai1 * B(1,1) + ai2 * B(2,1) + ai3 * B(3,1);
P(i,2) = ai0 * B(0,2) + ai1 * B(1,2) + ai2 * B(2,2) + ai3 * B(3,2);
P(i,3) = ai0 * B(0,3) + ai1 * B(1,3) + ai2 * B(2,3) + ai3 * B(3,3);
}
}
#undef A
#undef B
#undef P
#define A33(row,col) a[(col*3)+row]
#define B33(row,col) b[(col*3)+row]
#define P33(row,col) product[(col*3)+row]
///////////////////////////////////////////////////////////////////////////////
// Multiply two 3x3 matricies
void m3dMatrixMultiply33(M3DMatrix33f product, const M3DMatrix33f a, const M3DMatrix33f b )
{
for (int i = 0; i < 3; i++) {
float ai0=A33(i,0), ai1=A33(i,1), ai2=A33(i,2);
P33(i,0) = ai0 * B33(0,0) + ai1 * B33(1,0) + ai2 * B33(2,0);
P33(i,1) = ai0 * B33(0,1) + ai1 * B33(1,1) + ai2 * B33(2,1);
P33(i,2) = ai0 * B33(0,2) + ai1 * B33(1,2) + ai2 * B33(2,2);
}
}
// Ditto above, but for doubles
void m3dMatrixMultiply44(M3DMatrix33d product, const M3DMatrix33d a, const M3DMatrix33d b )
{
for (int i = 0; i < 3; i++) {
double ai0=A33(i,0), ai1=A33(i,1), ai2=A33(i,2);
P33(i,0) = ai0 * B33(0,0) + ai1 * B33(1,0) + ai2 * B33(2,0);
P33(i,1) = ai0 * B33(0,1) + ai1 * B33(1,1) + ai2 * B33(2,1);
P33(i,2) = ai0 * B33(0,2) + ai1 * B33(1,2) + ai2 * B33(2,2);
}
}
#undef A33
#undef B33
#undef P33
#define M33(row,col) m[col*3+row]
///////////////////////////////////////////////////////////////////////////////
// Creates a 3x3 rotation matrix, takes radians NOT degrees
void m3dRotationMatrix33(M3DMatrix33f m, float angle, float x, float y, float z)
{
float mag, s, c;
float xx, yy, zz, xy, yz, zx, xs, ys, zs, one_c;
s = float(sin(angle));
c = float(cos(angle));
mag = float(sqrt( x*x + y*y + z*z ));
// Identity matrix
if (mag == 0.0f) {
m3dLoadIdentity33(m);
return;
}
// Rotation matrix is normalized
x /= mag;
y /= mag;
z /= mag;
xx = x * x;
yy = y * y;
zz = z * z;
xy = x * y;
yz = y * z;
zx = z * x;
xs = x * s;
ys = y * s;
zs = z * s;
one_c = 1.0f - c;
M33(0,0) = (one_c * xx) + c;
M33(0,1) = (one_c * xy) - zs;
M33(0,2) = (one_c * zx) + ys;
M33(1,0) = (one_c * xy) + zs;
M33(1,1) = (one_c * yy) + c;
M33(1,2) = (one_c * yz) - xs;
M33(2,0) = (one_c * zx) - ys;
M33(2,1) = (one_c * yz) + xs;
M33(2,2) = (one_c * zz) + c;
}
#undef M33
///////////////////////////////////////////////////////////////////////////////
// Creates a 4x4 rotation matrix, takes radians NOT degrees
void m3dRotationMatrix44(M3DMatrix44f m, float angle, float x, float y, float z)
{
float mag, s, c;
float xx, yy, zz, xy, yz, zx, xs, ys, zs, one_c;
s = float(sin(angle));
c = float(cos(angle));
mag = float(sqrt( x*x + y*y + z*z ));
// Identity matrix
if (mag == 0.0f) {
m3dLoadIdentity44(m);
return;
}
// Rotation matrix is normalized
x /= mag;
y /= mag;
z /= mag;
#define M(row,col) m[col*4+row]
xx = x * x;
yy = y * y;
zz = z * z;
xy = x * y;
yz = y * z;
zx = z * x;
xs = x * s;
ys = y * s;
zs = z * s;
one_c = 1.0f - c;
M(0,0) = (one_c * xx) + c;
M(0,1) = (one_c * xy) - zs;
M(0,2) = (one_c * zx) + ys;
M(0,3) = 0.0f;
M(1,0) = (one_c * xy) + zs;
M(1,1) = (one_c * yy) + c;
M(1,2) = (one_c * yz) - xs;
M(1,3) = 0.0f;
M(2,0) = (one_c * zx) - ys;
M(2,1) = (one_c * yz) + xs;
M(2,2) = (one_c * zz) + c;
M(2,3) = 0.0f;
M(3,0) = 0.0f;
M(3,1) = 0.0f;
M(3,2) = 0.0f;
M(3,3) = 1.0f;
#undef M
}
///////////////////////////////////////////////////////////////////////////////
// Ditto above, but for doubles
void m3dRotationMatrix33(M3DMatrix33d m, double angle, double x, double y, double z)
{
double mag, s, c;
double xx, yy, zz, xy, yz, zx, xs, ys, zs, one_c;
s = sin(angle);
c = cos(angle);
mag = sqrt( x*x + y*y + z*z );
// Identity matrix
if (mag == 0.0) {
m3dLoadIdentity33(m);
return;
}
// Rotation matrix is normalized
x /= mag;
y /= mag;
z /= mag;
#define M(row,col) m[col*3+row]
xx = x * x;
yy = y * y;
zz = z * z;
xy = x * y;
yz = y * z;
zx = z * x;
xs = x * s;
ys = y * s;
zs = z * s;
one_c = 1.0 - c;
M(0,0) = (one_c * xx) + c;
M(0,1) = (one_c * xy) - zs;
M(0,2) = (one_c * zx) + ys;
M(1,0) = (one_c * xy) + zs;
M(1,1) = (one_c * yy) + c;
M(1,2) = (one_c * yz) - xs;
M(2,0) = (one_c * zx) - ys;
M(2,1) = (one_c * yz) + xs;
M(2,2) = (one_c * zz) + c;
#undef M
}
///////////////////////////////////////////////////////////////////////////////
// Creates a 4x4 rotation matrix, takes radians NOT degrees
void m3dRotationMatrix44(M3DMatrix44d m, double angle, double x, double y, double z)
{
double mag, s, c;
double xx, yy, zz, xy, yz, zx, xs, ys, zs, one_c;
s = sin(angle);
c = cos(angle);
mag = sqrt( x*x + y*y + z*z );
// Identity matrix
if (mag == 0.0) {
m3dLoadIdentity44(m);
return;
}
// Rotation matrix is normalized
x /= mag;
y /= mag;
z /= mag;
#define M(row,col) m[col*4+row]
xx = x * x;
yy = y * y;
zz = z * z;
xy = x * y;
yz = y * z;
zx = z * x;
xs = x * s;
ys = y * s;
zs = z * s;
one_c = 1.0f - c;
M(0,0) = (one_c * xx) + c;
M(0,1) = (one_c * xy) - zs;
M(0,2) = (one_c * zx) + ys;
M(0,3) = 0.0;
M(1,0) = (one_c * xy) + zs;
M(1,1) = (one_c * yy) + c;
M(1,2) = (one_c * yz) - xs;
M(1,3) = 0.0;
M(2,0) = (one_c * zx) - ys;
M(2,1) = (one_c * yz) + xs;
M(2,2) = (one_c * zz) + c;
M(2,3) = 0.0;
M(3,0) = 0.0;
M(3,1) = 0.0;
M(3,2) = 0.0;
M(3,3) = 1.0;
#undef M
}
// Lifted from Mesa
/*
* Compute inverse of 4x4 transformation matrix.
* Code contributed by Jacques Leroy [email protected]
* Return GL_TRUE for success, GL_FALSE for failure (singular matrix)
*/
bool m3dInvertMatrix44(M3DMatrix44f dst, const M3DMatrix44f src )
{
#define SWAP_ROWS(a, b) { float *_tmp = a; (a)=(b); (b)=_tmp; }
#define MAT(m,r,c) (m)[(c)*4+(r)]
float wtmp[4][8];
float m0, m1, m2, m3, s;
float *r0, *r1, *r2, *r3;
r0 = wtmp[0], r1 = wtmp[1], r2 = wtmp[2], r3 = wtmp[3];
r0[0] = MAT(src,0,0), r0[1] = MAT(src,0,1),
r0[2] = MAT(src,0,2), r0[3] = MAT(src,0,3),
r0[4] = 1.0, r0[5] = r0[6] = r0[7] = 0.0,
r1[0] = MAT(src,1,0), r1[1] = MAT(src,1,1),
r1[2] = MAT(src,1,2), r1[3] = MAT(src,1,3),
r1[5] = 1.0, r1[4] = r1[6] = r1[7] = 0.0,
r2[0] = MAT(src,2,0), r2[1] = MAT(src,2,1),
r2[2] = MAT(src,2,2), r2[3] = MAT(src,2,3),
r2[6] = 1.0, r2[4] = r2[5] = r2[7] = 0.0,
r3[0] = MAT(src,3,0), r3[1] = MAT(src,3,1),
r3[2] = MAT(src,3,2), r3[3] = MAT(src,3,3),
r3[7] = 1.0, r3[4] = r3[5] = r3[6] = 0.0;
/* choose pivot - or die */
if (fabs(r3[0])>fabs(r2[0])) SWAP_ROWS(r3, r2);
if (fabs(r2[0])>fabs(r1[0])) SWAP_ROWS(r2, r1);
if (fabs(r1[0])>fabs(r0[0])) SWAP_ROWS(r1, r0);
if (0.0 == r0[0]) return false;
/* eliminate first variable */
m1 = r1[0]/r0[0]; m2 = r2[0]/r0[0]; m3 = r3[0]/r0[0];
s = r0[1]; r1[1] -= m1 * s; r2[1] -= m2 * s; r3[1] -= m3 * s;
s = r0[2]; r1[2] -= m1 * s; r2[2] -= m2 * s; r3[2] -= m3 * s;
s = r0[3]; r1[3] -= m1 * s; r2[3] -= m2 * s; r3[3] -= m3 * s;
s = r0[4];
if (s != 0.0) { r1[4] -= m1 * s; r2[4] -= m2 * s; r3[4] -= m3 * s; }
s = r0[5];
if (s != 0.0) { r1[5] -= m1 * s; r2[5] -= m2 * s; r3[5] -= m3 * s; }
s = r0[6];
if (s != 0.0) { r1[6] -= m1 * s; r2[6] -= m2 * s; r3[6] -= m3 * s; }
s = r0[7];
if (s != 0.0) { r1[7] -= m1 * s; r2[7] -= m2 * s; r3[7] -= m3 * s; }
/* choose pivot - or die */
if (fabs(r3[1])>fabs(r2[1])) SWAP_ROWS(r3, r2);
if (fabs(r2[1])>fabs(r1[1])) SWAP_ROWS(r2, r1);
if (0.0 == r1[1]) return false;
/* eliminate second variable */
m2 = r2[1]/r1[1]; m3 = r3[1]/r1[1];
r2[2] -= m2 * r1[2]; r3[2] -= m3 * r1[2];
r2[3] -= m2 * r1[3]; r3[3] -= m3 * r1[3];
s = r1[4]; if (0.0 != s) { r2[4] -= m2 * s; r3[4] -= m3 * s; }
s = r1[5]; if (0.0 != s) { r2[5] -= m2 * s; r3[5] -= m3 * s; }
s = r1[6]; if (0.0 != s) { r2[6] -= m2 * s; r3[6] -= m3 * s; }
s = r1[7]; if (0.0 != s) { r2[7] -= m2 * s; r3[7] -= m3 * s; }
/* choose pivot - or die */
if (fabs(r3[2])>fabs(r2[2])) SWAP_ROWS(r3, r2);
if (0.0 == r2[2]) return false;
/* eliminate third variable */
m3 = r3[2]/r2[2];
r3[3] -= m3 * r2[3], r3[4] -= m3 * r2[4],
r3[5] -= m3 * r2[5], r3[6] -= m3 * r2[6],
r3[7] -= m3 * r2[7];
/* last check */
if (0.0 == r3[3]) return false;
s = 1.0f/r3[3]; /* now back substitute row 3 */
r3[4] *= s; r3[5] *= s; r3[6] *= s; r3[7] *= s;
m2 = r2[3]; /* now back substitute row 2 */
s = 1.0f/r2[2];
r2[4] = s * (r2[4] - r3[4] * m2), r2[5] = s * (r2[5] - r3[5] * m2),
r2[6] = s * (r2[6] - r3[6] * m2), r2[7] = s * (r2[7] - r3[7] * m2);
m1 = r1[3];
r1[4] -= r3[4] * m1, r1[5] -= r3[5] * m1,
r1[6] -= r3[6] * m1, r1[7] -= r3[7] * m1;
m0 = r0[3];
r0[4] -= r3[4] * m0, r0[5] -= r3[5] * m0,
r0[6] -= r3[6] * m0, r0[7] -= r3[7] * m0;
m1 = r1[2]; /* now back substitute row 1 */
s = 1.0f/r1[1];
r1[4] = s * (r1[4] - r2[4] * m1), r1[5] = s * (r1[5] - r2[5] * m1),
r1[6] = s * (r1[6] - r2[6] * m1), r1[7] = s * (r1[7] - r2[7] * m1);
m0 = r0[2];
r0[4] -= r2[4] * m0, r0[5] -= r2[5] * m0,
r0[6] -= r2[6] * m0, r0[7] -= r2[7] * m0;
m0 = r0[1]; /* now back substitute row 0 */
s = 1.0f/r0[0];
r0[4] = s * (r0[4] - r1[4] * m0), r0[5] = s * (r0[5] - r1[5] * m0),
r0[6] = s * (r0[6] - r1[6] * m0), r0[7] = s * (r0[7] - r1[7] * m0);
MAT(dst,0,0) = r0[4]; MAT(dst,0,1) = r0[5],
MAT(dst,0,2) = r0[6]; MAT(dst,0,3) = r0[7],
MAT(dst,1,0) = r1[4]; MAT(dst,1,1) = r1[5],
MAT(dst,1,2) = r1[6]; MAT(dst,1,3) = r1[7],
MAT(dst,2,0) = r2[4]; MAT(dst,2,1) = r2[5],
MAT(dst,2,2) = r2[6]; MAT(dst,2,3) = r2[7],
MAT(dst,3,0) = r3[4]; MAT(dst,3,1) = r3[5],
MAT(dst,3,2) = r3[6]; MAT(dst,3,3) = r3[7];
return true;
#undef MAT
#undef SWAP_ROWS
}
// Ditto above, but for doubles
bool m3dInvertMatrix44(M3DMatrix44d dst, const M3DMatrix44d src)
{
#define SWAP_ROWS(a, b) { double *_tmp = a; (a)=(b); (b)=_tmp; }
#define MAT(m,r,c) (m)[(c)*4+(r)]
double wtmp[4][8];
double m0, m1, m2, m3, s;
double *r0, *r1, *r2, *r3;
r0 = wtmp[0], r1 = wtmp[1], r2 = wtmp[2], r3 = wtmp[3];
r0[0] = MAT(src,0,0), r0[1] = MAT(src,0,1),
r0[2] = MAT(src,0,2), r0[3] = MAT(src,0,3),
r0[4] = 1.0, r0[5] = r0[6] = r0[7] = 0.0,
r1[0] = MAT(src,1,0), r1[1] = MAT(src,1,1),
r1[2] = MAT(src,1,2), r1[3] = MAT(src,1,3),
r1[5] = 1.0, r1[4] = r1[6] = r1[7] = 0.0,
r2[0] = MAT(src,2,0), r2[1] = MAT(src,2,1),
r2[2] = MAT(src,2,2), r2[3] = MAT(src,2,3),
r2[6] = 1.0, r2[4] = r2[5] = r2[7] = 0.0,
r3[0] = MAT(src,3,0), r3[1] = MAT(src,3,1),
r3[2] = MAT(src,3,2), r3[3] = MAT(src,3,3),
r3[7] = 1.0, r3[4] = r3[5] = r3[6] = 0.0;
// choose pivot - or die
if (fabs(r3[0])>fabs(r2[0])) SWAP_ROWS(r3, r2);
if (fabs(r2[0])>fabs(r1[0])) SWAP_ROWS(r2, r1);
if (fabs(r1[0])>fabs(r0[0])) SWAP_ROWS(r1, r0);
if (0.0 == r0[0]) return false;
// eliminate first variable
m1 = r1[0]/r0[0]; m2 = r2[0]/r0[0]; m3 = r3[0]/r0[0];
s = r0[1]; r1[1] -= m1 * s; r2[1] -= m2 * s; r3[1] -= m3 * s;
s = r0[2]; r1[2] -= m1 * s; r2[2] -= m2 * s; r3[2] -= m3 * s;
s = r0[3]; r1[3] -= m1 * s; r2[3] -= m2 * s; r3[3] -= m3 * s;
s = r0[4];
if (s != 0.0) { r1[4] -= m1 * s; r2[4] -= m2 * s; r3[4] -= m3 * s; }
s = r0[5];
if (s != 0.0) { r1[5] -= m1 * s; r2[5] -= m2 * s; r3[5] -= m3 * s; }
s = r0[6];
if (s != 0.0) { r1[6] -= m1 * s; r2[6] -= m2 * s; r3[6] -= m3 * s; }
s = r0[7];
if (s != 0.0) { r1[7] -= m1 * s; r2[7] -= m2 * s; r3[7] -= m3 * s; }
// choose pivot - or die
if (fabs(r3[1])>fabs(r2[1])) SWAP_ROWS(r3, r2);
if (fabs(r2[1])>fabs(r1[1])) SWAP_ROWS(r2, r1);
if (0.0 == r1[1]) return false;
// eliminate second variable
m2 = r2[1]/r1[1]; m3 = r3[1]/r1[1];
r2[2] -= m2 * r1[2]; r3[2] -= m3 * r1[2];
r2[3] -= m2 * r1[3]; r3[3] -= m3 * r1[3];
s = r1[4]; if (0.0 != s) { r2[4] -= m2 * s; r3[4] -= m3 * s; }
s = r1[5]; if (0.0 != s) { r2[5] -= m2 * s; r3[5] -= m3 * s; }
s = r1[6]; if (0.0 != s) { r2[6] -= m2 * s; r3[6] -= m3 * s; }
s = r1[7]; if (0.0 != s) { r2[7] -= m2 * s; r3[7] -= m3 * s; }
// choose pivot - or die
if (fabs(r3[2])>fabs(r2[2])) SWAP_ROWS(r3, r2);
if (0.0 == r2[2]) return false;
// eliminate third variable
m3 = r3[2]/r2[2];
r3[3] -= m3 * r2[3], r3[4] -= m3 * r2[4],
r3[5] -= m3 * r2[5], r3[6] -= m3 * r2[6],
r3[7] -= m3 * r2[7];
// last check
if (0.0 == r3[3]) return false;
s = 1.0f/r3[3]; // now back substitute row 3
r3[4] *= s; r3[5] *= s; r3[6] *= s; r3[7] *= s;
m2 = r2[3]; // now back substitute row 2
s = 1.0f/r2[2];
r2[4] = s * (r2[4] - r3[4] * m2), r2[5] = s * (r2[5] - r3[5] * m2),
r2[6] = s * (r2[6] - r3[6] * m2), r2[7] = s * (r2[7] - r3[7] * m2);
m1 = r1[3];
r1[4] -= r3[4] * m1, r1[5] -= r3[5] * m1,
r1[6] -= r3[6] * m1, r1[7] -= r3[7] * m1;
m0 = r0[3];
r0[4] -= r3[4] * m0, r0[5] -= r3[5] * m0,
r0[6] -= r3[6] * m0, r0[7] -= r3[7] * m0;
m1 = r1[2]; // now back substitute row 1
s = 1.0f/r1[1];
r1[4] = s * (r1[4] - r2[4] * m1), r1[5] = s * (r1[5] - r2[5] * m1),
r1[6] = s * (r1[6] - r2[6] * m1), r1[7] = s * (r1[7] - r2[7] * m1);
m0 = r0[2];
r0[4] -= r2[4] * m0, r0[5] -= r2[5] * m0,
r0[6] -= r2[6] * m0, r0[7] -= r2[7] * m0;
m0 = r0[1]; // now back substitute row 0
s = 1.0f/r0[0];
r0[4] = s * (r0[4] - r1[4] * m0), r0[5] = s * (r0[5] - r1[5] * m0),
r0[6] = s * (r0[6] - r1[6] * m0), r0[7] = s * (r0[7] - r1[7] * m0);
MAT(dst,0,0) = r0[4]; MAT(dst,0,1) = r0[5],
MAT(dst,0,2) = r0[6]; MAT(dst,0,3) = r0[7],
MAT(dst,1,0) = r1[4]; MAT(dst,1,1) = r1[5],
MAT(dst,1,2) = r1[6]; MAT(dst,1,3) = r1[7],
MAT(dst,2,0) = r2[4]; MAT(dst,2,1) = r2[5],
MAT(dst,2,2) = r2[6]; MAT(dst,2,3) = r2[7],
MAT(dst,3,0) = r3[4]; MAT(dst,3,1) = r3[5],
MAT(dst,3,2) = r3[6]; MAT(dst,3,3) = r3[7];
return true;
#undef MAT
#undef SWAP_ROWS
return true;
}
///////////////////////////////////////////////////////////////////////////////////////
// Get Window coordinates, discard Z...
void m3dProjectXY(const M3DMatrix44f mModelView, const M3DMatrix44f mProjection, const int iViewPort[4], const M3DVector3f vPointIn, M3DVector2f vPointOut)
{
M3DVector4f vBack, vForth;
memcpy(vBack, vPointIn, sizeof(float)*3);
vBack[3] = 1.0f;
m3dTransformVector4(vForth, vBack, mModelView);
m3dTransformVector4(vBack, vForth, mProjection);
if(!m3dCloseEnough(vBack[3], 0.0f, 0.000001f)) {
float div = 1.0f / vBack[3];
vBack[0] *= div;
vBack[1] *= div;
}
vPointOut[0] = vBack[0] * 0.5f + 0.5f;
vPointOut[1] = vBack[1] * 0.5f + 0.5f;
/* Map x,y to viewport */
vPointOut[0] = (vPointOut[0] * iViewPort[2]) + iViewPort[0];
vPointOut[1] = (vPointOut[1] * iViewPort[3]) + iViewPort[1];
}
///////////////////////////////////////////////////////////////////////////////////////
// Get window coordinates, we also want Z....
void m3dProjectXYZ(const M3DMatrix44f mModelView, const M3DMatrix44f mProjection, const int iViewPort[4], const M3DVector3f vPointIn, M3DVector3f vPointOut)
{
M3DVector4f vBack, vForth;
memcpy(vBack, vPointIn, sizeof(float)*3);
vBack[3] = 1.0f;
m3dTransformVector4(vForth, vBack, mModelView);
m3dTransformVector4(vBack, vForth, mProjection);
if(!m3dCloseEnough(vBack[3], 0.0f, 0.000001f)) {
float div = 1.0f / vBack[3];
vBack[0] *= div;
vBack[1] *= div;
vBack[2] *= div;
}
vPointOut[0] = vBack[0] * 0.5f + 0.5f;
vPointOut[1] = vBack[1] * 0.5f + 0.5f;
vPointOut[2] = vBack[2] * 0.5f + 0.5f;
/* Map x,y to viewport */
vPointOut[0] = (vPointOut[0] * iViewPort[2]) + iViewPort[0];
vPointOut[1] = (vPointOut[1] * iViewPort[3]) + iViewPort[1];
}
///////////////////////////////////////////////////////////////////////////////
///////////////////////////////////////////////////////////////////////////////
// Misc. Utilities
///////////////////////////////////////////////////////////////////////////////
// Calculates the normal of a triangle specified by the three points
// p1, p2, and p3. Each pointer points to an array of three floats. The
// triangle is assumed to be wound counter clockwise.
void m3dFindNormal(M3DVector3f result, const M3DVector3f point1, const M3DVector3f point2,
const M3DVector3f point3)
{
M3DVector3f v1,v2; // Temporary vectors
// Calculate two vectors from the three points. Assumes counter clockwise
// winding!
v1[0] = point1[0] - point2[0];
v1[1] = point1[1] - point2[1];
v1[2] = point1[2] - point2[2];
v2[0] = point2[0] - point3[0];
v2[1] = point2[1] - point3[1];
v2[2] = point2[2] - point3[2];
// Take the cross product of the two vectors to get
// the normal vector.
m3dCrossProduct(result, v1, v2);
}
// Ditto above, but for doubles
void m3dFindNormal(M3DVector3d result, const M3DVector3d point1, const M3DVector3d point2,
const M3DVector3d point3)
{
M3DVector3d v1,v2; // Temporary vectors
// Calculate two vectors from the three points. Assumes counter clockwise
// winding!
v1[0] = point1[0] - point2[0];
v1[1] = point1[1] - point2[1];
v1[2] = point1[2] - point2[2];
v2[0] = point2[0] - point3[0];
v2[1] = point2[1] - point3[1];
v2[2] = point2[2] - point3[2];
// Take the cross product of the two vectors to get
// the normal vector.
m3dCrossProduct(result, v1, v2);
}
/////////////////////////////////////////////////////////////////////////////////////////
// Calculate the plane equation of the plane that the three specified points lay in. The
// points are given in clockwise winding order, with normal pointing out of clockwise face
// planeEq contains the A,B,C, and D of the plane equation coefficients
void m3dGetPlaneEquation(M3DVector4f planeEq, const M3DVector3f p1, const M3DVector3f p2, const M3DVector3f p3)
{
// Get two vectors... do the cross product
M3DVector3f v1, v2;
// V1 = p3 - p1
v1[0] = p3[0] - p1[0];
v1[1] = p3[1] - p1[1];
v1[2] = p3[2] - p1[2];
// V2 = P2 - p1
v2[0] = p2[0] - p1[0];
v2[1] = p2[1] - p1[1];
v2[2] = p2[2] - p1[2];
// Unit normal to plane - Not sure which is the best way here
m3dCrossProduct(planeEq, v1, v2);
m3dNormalizeVector(planeEq);
// Back substitute to get D
planeEq[3] = -(planeEq[0] * p3[0] + planeEq[1] * p3[1] + planeEq[2] * p3[2]);
}
// Ditto above, but for doubles
void m3dGetPlaneEquation(M3DVector4d planeEq, const M3DVector3d p1, const M3DVector3d p2, const M3DVector3d p3)
{
// Get two vectors... do the cross product
M3DVector3d v1, v2;
// V1 = p3 - p1
v1[0] = p3[0] - p1[0];
v1[1] = p3[1] - p1[1];
v1[2] = p3[2] - p1[2];
// V2 = P2 - p1
v2[0] = p2[0] - p1[0];
v2[1] = p2[1] - p1[1];
v2[2] = p2[2] - p1[2];
// Unit normal to plane - Not sure which is the best way here
m3dCrossProduct(planeEq, v1, v2);
m3dNormalizeVector(planeEq);
// Back substitute to get D
planeEq[3] = -(planeEq[0] * p3[0] + planeEq[1] * p3[1] + planeEq[2] * p3[2]);
}
//////////////////////////////////////////////////////////////////////////////////////////////////
// This function does a three dimensional Catmull-Rom curve interpolation. Pass four points, and a
// floating point number between 0.0 and 1.0. The curve is interpolated between the middle two points.
// Coded by RSW
// http://www.mvps.org/directx/articles/catmull/
void m3dCatmullRom3(M3DVector3f vOut, M3DVector3f vP0, M3DVector3f vP1, M3DVector3f vP2, M3DVector3f vP3, float t)
{
// Unrolled loop to speed things up a little bit...
float t2 = t * t;
float t3 = t2 * t;
// X
vOut[0] = 0.5f * ( ( 2.0f * vP1[0]) +
(-vP0[0] + vP2[0]) * t +
(2.0f * vP0[0] - 5.0f *vP1[0] + 4.0f * vP2[0] - vP3[0]) * t2 +
(-vP0[0] + 3.0f*vP1[0] - 3.0f *vP2[0] + vP3[0]) * t3);
// Y
vOut[1] = 0.5f * ( ( 2.0f * vP1[1]) +
(-vP0[1] + vP2[1]) * t +
(2.0f * vP0[1] - 5.0f *vP1[1] + 4.0f * vP2[1] - vP3[1]) * t2 +
(-vP0[1] + 3.0f*vP1[1] - 3.0f *vP2[1] + vP3[1]) * t3);
// Z
vOut[2] = 0.5f * ( ( 2.0f * vP1[2]) +
(-vP0[2] + vP2[2]) * t +
(2.0f * vP0[2] - 5.0f *vP1[2] + 4.0f * vP2[2] - vP3[2]) * t2 +
(-vP0[2] + 3.0f*vP1[2] - 3.0f *vP2[2] + vP3[2]) * t3);
}
//////////////////////////////////////////////////////////////////////////////////////////////////
// This function does a three dimensional Catmull-Rom curve interpolation. Pass four points, and a
// floating point number between 0.0 and 1.0. The curve is interpolated between the middle two points.
// Coded by RSW
// http://www.mvps.org/directx/articles/catmull/
void m3dCatmullRom3(M3DVector3d vOut, M3DVector3d vP0, M3DVector3d vP1, M3DVector3d vP2, M3DVector3d vP3, double t)
{
// Unrolled loop to speed things up a little bit...
double t2 = t * t;
double t3 = t2 * t;
// X
vOut[0] = 0.5 * ( ( 2.0 * vP1[0]) +
(-vP0[0] + vP2[0]) * t +
(2.0 * vP0[0] - 5.0 *vP1[0] + 4.0 * vP2[0] - vP3[0]) * t2 +
(-vP0[0] + 3.0*vP1[0] - 3.0 *vP2[0] + vP3[0]) * t3);
// Y
vOut[1] = 0.5 * ( ( 2.0 * vP1[1]) +
(-vP0[1] + vP2[1]) * t +
(2.0 * vP0[1] - 5.0 *vP1[1] + 4.0 * vP2[1] - vP3[1]) * t2 +
(-vP0[1] + 3*vP1[1] - 3.0 *vP2[1] + vP3[1]) * t3);
// Z
vOut[2] = 0.5 * ( ( 2.0 * vP1[2]) +
(-vP0[2] + vP2[2]) * t +
(2.0 * vP0[2] - 5.0 *vP1[2] + 4.0 * vP2[2] - vP3[2]) * t2 +
(-vP0[2] + 3.0*vP1[2] - 3.0 *vP2[2] + vP3[2]) * t3);
}
///////////////////////////////////////////////////////////////////////////////
// Determine if the ray (starting at point) intersects the sphere centered at
// sphereCenter with radius sphereRadius
// Return value is < 0 if the ray does not intersect
// Return value is 0.0 if ray is tangent
// Positive value is distance to the intersection point
// Algorithm from "3D Math Primer for Graphics and Game Development"
double m3dRaySphereTest(const M3DVector3d point, const M3DVector3d ray, const M3DVector3d sphereCenter, double sphereRadius)
{
//m3dNormalizeVector(ray); // Make sure ray is unit length
M3DVector3d rayToCenter; // Ray to center of sphere
rayToCenter[0] = sphereCenter[0] - point[0];
rayToCenter[1] = sphereCenter[1] - point[1];
rayToCenter[2] = sphereCenter[2] - point[2];
// Project rayToCenter on ray to test
double a = m3dDotProduct(rayToCenter, ray);
// Distance to center of sphere
double distance2 = m3dDotProduct(rayToCenter, rayToCenter); // Or length
double dRet = (sphereRadius * sphereRadius) - distance2 + (a*a);
if(dRet > 0.0) // Return distance to intersection
dRet = a - sqrt(dRet);
return dRet;
}
///////////////////////////////////////////////////////////////////////////////
// Determine if the ray (starting at point) intersects the sphere centered at
// ditto above, but uses floating point math
float m3dRaySphereTest(const M3DVector3f point, const M3DVector3f ray, const M3DVector3f sphereCenter, float sphereRadius)
{
//m3dNormalizeVectorf(ray); // Make sure ray is unit length
M3DVector3f rayToCenter; // Ray to center of sphere
rayToCenter[0] = sphereCenter[0] - point[0];
rayToCenter[1] = sphereCenter[1] - point[1];
rayToCenter[2] = sphereCenter[2] - point[2];
// Project rayToCenter on ray to test
float a = m3dDotProduct(rayToCenter, ray);
// Distance to center of sphere
float distance2 = m3dDotProduct(rayToCenter, rayToCenter); // Or length
float dRet = (sphereRadius * sphereRadius) - distance2 + (a*a);
if(dRet > 0.0) // Return distance to intersection
dRet = a - sqrtf(dRet);
return dRet;
}
///////////////////////////////////////////////////////////////////////////////////////////////////
// Calculate the tangent basis for a triangle on the surface of a model
// This vector is needed for most normal mapping shaders
void m3dCalculateTangentBasis(const M3DVector3f vTriangle[3], const M3DVector2f vTexCoords[3], const M3DVector3f N, M3DVector3f vTangent)
{
M3DVector3f dv2v1, dv3v1;
float dc2c1t, dc2c1b, dc3c1t, dc3c1b;
float M;
m3dSubtractVectors3(dv2v1, vTriangle[1], vTriangle[0]);
m3dSubtractVectors3(dv3v1, vTriangle[2], vTriangle[0]);
dc2c1t = vTexCoords[1][0] - vTexCoords[0][0];
dc2c1b = vTexCoords[1][1] - vTexCoords[0][1];
dc3c1t = vTexCoords[2][0] - vTexCoords[0][0];
dc3c1b = vTexCoords[2][1] - vTexCoords[0][1];
M = (dc2c1t * dc3c1b) - (dc3c1t * dc2c1b);
M = 1.0f / M;
m3dScaleVector3(dv2v1, dc3c1b);
m3dScaleVector3(dv3v1, dc2c1b);
m3dSubtractVectors3(vTangent, dv2v1, dv3v1);
m3dScaleVector3(vTangent, M); // This potentially changes the direction of the vector
m3dNormalizeVector(vTangent);
M3DVector3f B;
m3dCrossProduct(B, N, vTangent);
m3dCrossProduct(vTangent, B, N);
m3dNormalizeVector(vTangent);
}
////////////////////////////////////////////////////////////////////////////
// Smoothly step between 0 and 1 between edge1 and edge 2
double m3dSmoothStep(double edge1, double edge2, double x)
{
double t;
t = (x - edge1) / (edge2 - edge1);
if(t > 1.0)
t = 1.0;
if(t < 0.0)
t = 0.0f;
return t * t * ( 3.0 - 2.0 * t);
}
////////////////////////////////////////////////////////////////////////////
// Smoothly step between 0 and 1 between edge1 and edge 2
float m3dSmoothStep(float edge1, float edge2, float x)
{
float t;
t = (x - edge1) / (edge2 - edge1);
if(t > 1.0f)
t = 1.0f;
if(t < 0.0)
t = 0.0f;
return t * t * ( 3.0f - 2.0f * t);
}
///////////////////////////////////////////////////////////////////////////
// Creae a projection to "squish" an object into the plane.
// Use m3dGetPlaneEquationf(planeEq, point1, point2, point3);
// to get a plane equation.
void m3dMakePlanarShadowMatrix(M3DMatrix44f proj, const M3DVector4f planeEq, const M3DVector3f vLightPos)
{
// These just make the code below easier to read. They will be
// removed by the optimizer.
float a = planeEq[0];
float b = planeEq[1];
float c = planeEq[2];
float d = planeEq[3];
float dx = -vLightPos[0];
float dy = -vLightPos[1];
float dz = -vLightPos[2];
// Now build the projection matrix
proj[0] = b * dy + c * dz;
proj[1] = -a * dy;
proj[2] = -a * dz;
proj[3] = 0.0;
proj[4] = -b * dx;
proj[5] = a * dx + c * dz;
proj[6] = -b * dz;
proj[7] = 0.0;
proj[8] = -c * dx;
proj[9] = -c * dy;
proj[10] = a * dx + b * dy;
proj[11] = 0.0;
proj[12] = -d * dx;
proj[13] = -d * dy;
proj[14] = -d * dz;
proj[15] = a * dx + b * dy + c * dz;
// Shadow matrix ready
}
///////////////////////////////////////////////////////////////////////////
// Creae a projection to "squish" an object into the plane.
// Use m3dGetPlaneEquationd(planeEq, point1, point2, point3);
// to get a plane equation.
void m3dMakePlanarShadowMatrix(M3DMatrix44d proj, const M3DVector4d planeEq, const M3DVector3f vLightPos)
{
// These just make the code below easier to read. They will be
// removed by the optimizer.
double a = planeEq[0];
double b = planeEq[1];
double c = planeEq[2];
double d = planeEq[3];
double dx = -vLightPos[0];
double dy = -vLightPos[1];
double dz = -vLightPos[2];
// Now build the projection matrix
proj[0] = b * dy + c * dz;
proj[1] = -a * dy;
proj[2] = -a * dz;
proj[3] = 0.0;
proj[4] = -b * dx;
proj[5] = a * dx + c * dz;
proj[6] = -b * dz;
proj[7] = 0.0;
proj[8] = -c * dx;
proj[9] = -c * dy;
proj[10] = a * dx + b * dy;
proj[11] = 0.0;
proj[12] = -d * dx;
proj[13] = -d * dy;
proj[14] = -d * dz;
proj[15] = a * dx + b * dy + c * dz;
// Shadow matrix ready
}
/////////////////////////////////////////////////////////////////////////////
// I want to know the point on a ray, closest to another given point in space.
// As a bonus, return the distance squared of the two points.
// In: vRayOrigin is the origin of the ray.
// In: vUnitRayDir is the unit vector of the ray
// In: vPointInSpace is the point in space
// Out: vPointOnRay is the poing on the ray closest to vPointInSpace
// Return: The square of the distance to the ray
double m3dClosestPointOnRay(M3DVector3d vPointOnRay, const M3DVector3d vRayOrigin, const M3DVector3d vUnitRayDir,
const M3DVector3d vPointInSpace)
{
M3DVector3d v;
m3dSubtractVectors3(v, vPointInSpace, vRayOrigin);
double t = m3dDotProduct(vUnitRayDir, v);
// This is the point on the ray
vPointOnRay[0] = vRayOrigin[0] + (t * vUnitRayDir[0]);
vPointOnRay[1] = vRayOrigin[1] + (t * vUnitRayDir[1]);
vPointOnRay[2] = vRayOrigin[2] + (t * vUnitRayDir[2]);
return m3dGetDistanceSquared(vPointOnRay, vPointInSpace);
}
// ditto above... but with floats
float m3dClosestPointOnRay(M3DVector3f vPointOnRay, const M3DVector3f vRayOrigin, const M3DVector3f vUnitRayDir,
const M3DVector3f vPointInSpace)
{
M3DVector3f v;
m3dSubtractVectors3(v, vPointInSpace, vRayOrigin);
float t = m3dDotProduct(vUnitRayDir, v);
// This is the point on the ray
vPointOnRay[0] = vRayOrigin[0] + (t * vUnitRayDir[0]);
vPointOnRay[1] = vRayOrigin[1] + (t * vUnitRayDir[1]);
vPointOnRay[2] = vRayOrigin[2] + (t * vUnitRayDir[2]);
return m3dGetDistanceSquared(vPointOnRay, vPointInSpace);
}