基于临界灰度值和亚像素的“边缘寻找”算法
基于临界灰度值和亚像素的“边缘寻找”算法
本文将围绕一个实例,主要就测量物体长度的算法加以阐述。现在假设我们要在图像中测量物体的长度。如图1所示,虚线内为图像范围,图中背景为白色,被测物呈黑色。 
图1 待测物体情况
在相机拍照后,将图像视频信号传至视觉卡,由视觉卡把波状视频信号翻译成数字信号,存到电脑的内存中去。储存信息如图2所示,图像中的虚线格子为像素单元。下面将具体说明基于临界灰度值和亚像素的边缘寻找算法。
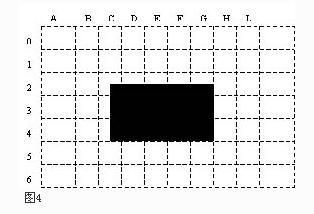
图2 内存中的存储信息
1、系统的自学习接下来第一步,我们要先选取一个临界灰度值(threshold,有关这个名词的解释,请参阅主题文章“视觉系统速成”)。大家已经知道,当图像转换成数字信号存到内存中去之后,我们便可以轻易地读取任何像素的灰度值。比如,我们现在从图像中得到行3的全部像素灰度值(如图3所示)。为了方便,这里假定此系统的灰度值分辨率是256级,0为最黑,255为最白。
图3 图像中第三行的像素灰度值情况[/center] 从图中,我们可以看出被测体的范围(X轴方向)是从列D至列H。在行3的灰度值中,从列D到列H的灰度值分别为:50,40,40,35,80。由此可知,被测物体在成像中灰度值最高(即颜色最白)的像素的灰度值是像素(3,H)的灰度值,即80。
那么我们便可以认为,系统的临界灰度值就是80,当然在实际测量中为留一定余地,我们不妨设为100。当然,若成像中被测物为白色,则应当选颜色最黑的地方的像素值为临界灰度值(有关临界灰度值设定的具体方法,以后另题讨论)。设定临界灰度值后,系统便完成了测量的第一步:自学习。假如此时已经完成了系统的标定工作(包括相机标定、系统标定),那么现在就可以正式开始测量了。
2、测量中的临界灰度值算法我们把一个待测的被测物放到相机下拍照。在内存中所得图像如图4所示。这里图4与图2略有不同。这只是为了说明在实际操作中,每次拍照所得到的图像,必定是有所不同的。
图4 得到图像后,我们便可以让软件对图像进行分析。仍是以行3为例,假设系统是从行3开始进行逐点扫描的。扫描的过程如下:先读取像素(3,A)的灰度值来与刚才所设定的临界灰度值作比较。如果像素(3,A)大过临界灰度值,也就是说像素(3,A)的颜色比临界灰度值白。那么这个像素就不是被测物上的一个点。然后就继续进行下一步的运算,读取像素(3,B)的灰度值重复上述运算,如此循环直至图像尽头列L。基本程序可描述如下:
for (I=A I<=L I ++)
{ if(pixel[3,I] <= 100)
{ flag = TRUE break }
}
程序中的100就是刚才系统所设定的临界灰度值。Flag是一个标志,当系统找到被测物的第一个边缘时,flag = TRUE,于是系统便开始寻找第二个边缘。在本例中,第一个边缘是由白到黑,第二个边缘是由黑到白。 假设在新的图像中,行3的灰度值如图5如示。那么系统扫描到像素(3,D)时,程序便会中断,flag = TRUE, 并开始寻找第二个由黑到白的边缘。
图5 新的图像灰度值情况
第二次寻找基本程序如下:
for (J=I J<=L J ++)
{ if(pixel[3,J] >= 100)
{ flag = FALSE break }
}
按图5所示,第二边缘的寻找,进行到像素(3,H)时,便自动停止。现在我们根据程序运行中第一个变量I所记录的数值,知道第一个边缘为D。由变量J知道第二个边缘是H-1=G。由此,可以知道整个被测物X轴方向的大小=G-D=4个像素。4×像素值(由系统标定得到),我们就最终得到被测物体的左右长度了。
但事情并没有这么简单,现在真正的问题出现了。实际上,不难发现在图4中,被测物实际上从列C开始的。只不过在列C中,被测物只有一部分,而另一部分是白色的背景。下面,我们就要设计新的算法,即“亚像素算法”来计算这种“一半一半”的部分。
3、亚像素算法亚像素算法的基本思路就是将一个像素再分为更小的单位。在我们上面的讨论中,一直以8bit的系统作例子,也就是说1个像素的灰度值分为256级。所以,以这类系统为例,进行亚像素计算就要把像素分为255个小单位。 或许,可以这样来理解“亚像素算法”。一个像素的灰度值从0到255,0是纯黑,255是纯白。不妨把像素想像成是一个由255个小像素所组成的集合。而每个小像素都是一个独立的小镜子,那就是说一个像素里面有255个小镜子。
灰度值则可以看作反光的小镜子数量:0表示255个小镜子全都没有反光;255表示255个镜子一起反光。上面讲到的所设定的临界灰度值100,则可表示255个镜子中有100个在反光,另外155个镜子没有反光。 现在,回到上面的测量例子中来。
从图4中可以看到,被测物在列C中只有一半,而正是由于这个原因所以列C的灰度值是高于临界灰度值的。只要我们把这部分也算到最终测量数据中去,所得到的结果必定更为准确。由此大家可以知道,真正的计算被测物的长度公式,并不是(像素数量×像素值)这么简单,而应该是((像素数量+第一边缘亚像素值+第二边缘亚像素值)×像素值),具体到本例,被测物左右真实长度=((4+像素(3,C)亚像素值+像素(3,H)亚像素值)×像素值)。
如何算亚像素值呢?非常简单,亚像素值(白色部分)=该像素灰度值/256;亚像素值(黑色部分)=1-亚像素值(白色部分);仍以图4为例,像素(3,C)的亚像素值=1-(120 / 256)=0.53; 像素(3,H)的亚像素值=1-(180/256)=0.3。而整个被测物左右实际长度为4.83个像素。其实就是在算有几个镜子在反光,有几个没反光罢了。
另外,除了这种计算方法,还有其他几种计算亚像素值的方法:
(1)亚像素值(白色部分)=(该像素灰度值×(临界灰度值/256))/256 亚像素值(黑色部分)=1-亚像素值(白色部分)
(2)亚像素值(白色部分)=后像素值/ (前像素值 +后像素值)亚像素值(黑色部分)=1-亚像素值(白色部分)
(3)亚像素值(白色部分)=(像素值-前像素值)/ (后像素值-前像素值) 亚像素值(黑色部分)=1-亚像素值(白色部分) 以上就是亚像素算法的基本原理。
在结束这个算法讨论之前,有两点必须注意:一是在实际情况下,大家不可能看到图4中所显示的情况,即像素的一半是黑色另一半是白色,这只是为了方便大家理解所画出来的,而真实的情况是一个像素就只是一小块灰色,没有明暗的分别。明暗的区别只能在像素与像素间显现出来;二是在描述亚像素的基本算法时,所说“小镜子”的概念完全是为了方便大家理解,比纯数学语言表达更为易懂。