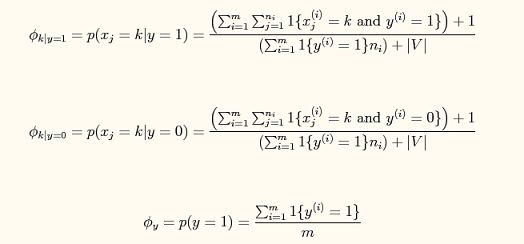机器学习练习之朴素贝叶斯

     练习来自http://openclassroom.stanford.edu/MainFolder/DocumentPage.php?course=MachineLearning&doc=exercises/ex6/ex6.html

贝叶斯定理

         贝叶斯定理是概率论中非常重要的定理， 数学家Harold Jeffreys曾说"Bayes therom is the theory of probability what pythagoras's therom is to geometry"。

        

       贝叶斯定理是基于条件概率的：

    

        而贝叶斯公式如下：

      （来自http://www2.imm.dtu.dk/courses/02443/slides2014/Bayes_HO.pdf）

       贝叶斯定理是教我们从现象中去推断本质或原因的一种方法。假设我们已经有了历史数据(x, y)，x可以看作是现象或事件，y是本质或原因，然后给出新的x，要推断出y是什么。比如贝叶斯可以用于医疗诊断，医疗的历史数据使我们知道在病人得了某种病后会有哪些症状、以及病种的分布情况，当有一个未确诊的病人出现时，根据病人发生的症状我们就可以推测病人患各种病的概率。

      贝叶斯定理涉及到先验概率、后验概率。先验概率是通过历史数据产生的，对于上面的贝叶斯公式，就是y的分布，一般而言y是离散的。P(y)是对历史数据y的似然估计。先验概率告诉我们，随便给出一个样本，y的概率分布。后验概率是根据观察数据x去推断y的概率分布。所以PRML书上说，posterior ∝ likelihood × prior。贝叶斯定理融合了先验概率和极大似然估计，极大似然估计就是likelihood，比如给出训练数据，likelihood可以得出最可能的模型，但是贝叶斯还考虑了先验概率，虽然那个似然最大的模型最大概率产生数据，但是如果那个模型很少见，概率很低，这样综合考虑起来就可能不是最优的模型。

        如果历史数据是无穷的，那么给出x，我们只要找到使得P(x|y)最大的y就行了，这就是频率论的最大似然估计，在机器学习中，-logP(x|y)就是损失函数，所以最大似然估计就是要最小化损失。贝叶斯定理的一个特点是融合了先验分布P(y), 频率学派认为这个是为了数学的方便而不是真实先验的反映，而且错误的先验选择可能导致错误的结果具有很高的置信度（参考PRML).

朴素贝叶斯

   朴素贝叶斯是基于贝叶斯定理与特征条件独立假设的分类方法，对于给定的训练数据集，首先基于特征条件独立假设学习输入/输出的联合概率分布，然后基于此模型，对给定的输入x，利用贝叶斯定理求出后验概率最大的输出y。朴素贝叶斯法实现简单，学习与预测的效率都很高，是一种常用的方法。（参见《统计学习方法》朴素贝叶斯法）。

   朴素贝叶斯法是属于生成模型，什么是生成模型呢？在监督学习中，我们要学到一个模型，使用这个模型，对于给定的输入可以预测相应的输出。模型的一般形式为决策函数Y=f(X)或条件概率分布f(Y|X)。生成模型的特点是要生成或可以还原联合概率分布p(x,y)，比如这里的贝叶斯法是能够学习到p(x,y)的，而判别模型则不能，像logistic regression就是判别模型，模型可以得到p(y|x)的概率，像感知机模型，只要算出w*x+b就能知道属于那个类别，这也是判别模型。

       好了， 回到本文的练习，这个练习是要用朴素贝叶斯法对邮件进行分类（垃圾邮件、非垃圾邮件）。

对于这个问题，朴素贝叶斯法的模型为：

 

        给定了邮件训练数据，可以求出垃圾邮件和非垃圾邮件的先验分布，也可以分别求出垃圾邮件和非垃圾邮件中每个词出现的概率。朴素贝叶斯的”朴素“就是认为每个词出现是独立的，与其它词的出现没有关系。垃圾邮件和非垃圾邮件对整个词库有不一样的分布情况，对于（非）垃圾邮件，全部词出现的概率加起来是等于1的，这又像是多项式分布了。在计算词在每个类别的概率时，用到了拉普拉斯平滑，这是为了防止在给新邮件进行计算它属于（非）垃圾邮件的概率，遇到了没有在训练数据见过的单词时，概率为0，这样乘起来结果就是0，所以预定给每个单词出现次数加1，这样为了概率和为1，分母中加了总词数。上图中的前两个公式是对于词库中的每个词在垃圾邮件和非垃圾邮件出现的全部词中的概率。由于每个单词出现的概率可能很低，为了防止下溢，使用自然对数进行计算。

    

     

邮件分类程序

%% Exercise 6: Naive Bayes
% 朴素贝叶斯练习：垃圾邮件分类
% Multinomial Naive Bayes model

numTrainDocs = 700;  % 文档数量
numTokens = 2500;  % 词库

 %读取训练集特征文件，每行有3个元素，表示文档id、词id和词频
 %dlmread读取以ascii码分割的文件中的数字
M = dlmread('train-features.txt', ''); 

%根据训练集特征构建稀疏矩阵，矩阵大小为numTrainDocs*numTokens
%S = sparse(i,j,s,m,n), i,j为向量，S(i(k),j(k))=s(k),S大小为m*n
%表示形式为:(i(k) j(k)) s(k)
spmatrix = sparse(M(:,1), M(:,2), M(:,3), numTrainDocs, numTokens); 

% 根据稀疏矩阵还原完整矩阵
train_matrix = full(spmatrix);

%读取文档类别
train_labels = dlmread('train-labels.txt');

% 训练过程
spam_index = find(train_labels);   %记录垃圾邮件索引
nonspam_index = find(train_labels==0);  %记录非垃圾邮件索引

proc_spam = length(spam_index)/numTrainDocs; % 计算垃圾邮件概率
% 分别计算垃圾和非垃圾邮件中每个单词出现的次数
% train_matrix(spam_index,:)找出属于垃圾邮件的文档向量
% sum(train_matrix(spam_index, :))对每一列的所有行累加起来，即统计该词在垃圾邮件中出现的总次数
wc_spam = sum(train_matrix(spam_index, :));
wc_nonspam = sum(train_matrix(nonspam_index, :));
% 分别计算tokens在垃圾邮件和非垃圾邮件中出现的概率
prob_tokens_spam = (wc_spam + 1) ./ (sum(wc_spam) + numTokens);
prob_tokens_nonspam = (wc_nonspam + 1) ./ (sum(wc_nonspam) + numTokens);

% 测试
test_labels = dlmread('test-labels.txt');

M = dlmread('test-features.txt', '');
% 构建稀疏矩阵，这么貌似有个问题，如果测试文档中不含有第2500个词的话，构建出的稀疏矩阵列数不是numTokens
% 下面的test_matrix乘于训练出来的(log(spam_wc_proc))'就肯定会出错
spmatrix = sparse(M(:,1), M(:,2), M(:,3));

test_matrix = full(spmatrix);

% 分别计算test_matrix的每一行即每篇文档属于垃圾邮件和非垃圾邮件的概率
% logp(x|y=1) + logp(y=1)
test_spam_proc = test_matrix * (log(prob_tokens_spam))' + log(proc_spam);
% logp(x|y=0) + logp(y=0)
test_nonspam_proc = test_matrix * (log(prob_tokens_nonspam))' + log(1-proc_spam);
% 预测
test_spam = test_spam_proc > test_nonspam_proc;
% 计算分类准确率
accuracy = sum(test_spam==test_labels) / length(test_labels);
fprintf('Accuracy:%f\n', accuracy);

实验有3个训练集，分别包括50、100和400封邮件的，实验结果表明使用越多的训练集，在同一测试集上的结果的准确率越高。