AI Planning
AI Planning
Theworld is:
1) dynamic
2) stochastic
3) partially observable
Actions:
1) take time
2) continuous effect
1 classical planning:
1.1 Assume: none of the above.
1.2 Modeling:
- States described by propositions currentlytrue
• Actions: general statetransformations described by
sets of pre- and post-conditions
• Represents a state-transitionsystem (but more
compact)
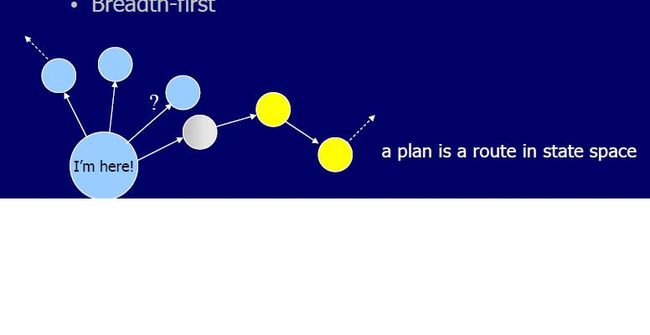
1.3planning: planning is searching
regression : from goal state to initialsate
forwarding: from initial sate to goal state
search method: BFS and DFS
1.4 STRIPS( s, g ) algorithm.
returns: a sequence of actions thattransforms s into g
1. Calculate the difference setd=g-s.
1. If d is empty, return an emptyplan
2. Choose action a whose add-listhas most formulas contained in g
3. p’ = STRIPS( s, precondition of a)
4. Compute the new state s’ byapplying p’ and a to s.
5. p = STRIPS( s’, g )
6. return p’;a;p
1.5 Refinement planning template
Refineplan( P : Plan set)
1. If P is empty, Fail.
2. If a minimal candidate of P is asolution, return it. End
3. Select a refinement strategy R
4. Apply R to P to get a new planset P’
5. Call Refineplan(P’ )
Termination ensured if R complete andmonotonic.
Existing Refinement Strategies
• State space refinement: e.g.STRIPS
• Plan space refinement: e.g. Leastcommitment
planning
• Task refinement: e.g. HTN
2 Stochastic environment
Ina stochastic environment, we use MDP to model and plan.
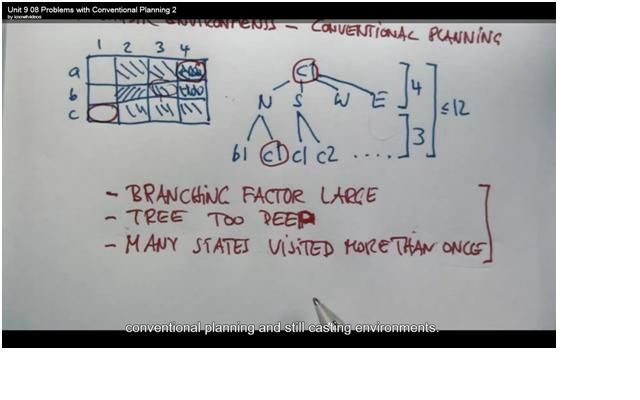
2.1 The issue using conventional planning in stochasticenvironment:
1)The branch factor is too large.
2)The tree is very deep.
3)Many states visited more than once
2.2 The MDP in stochastic environment
usage: robot navigation. Planning from x toy in a stochastic environments
sin {states,};
ain {actions(s)}; State Transition: T(S,a, S');
2.2.1:modeling:
Fully observable: S, A
Stochastic in state transition: T(S,a, S') = Pr(S'|S,a)
Reward in state S: R(S)- This is a short term and primitive value onpolicy.
2.2 find planning
Howto find a planning in MDP? or how to solve MDP?
Here we introduce some other value to solveMDP.
policy in state S: π(s)->the actiontaken in state s.
Value of state (node): Vπ(s):expected total reward in state s after policy π. This is a long term evaluate function of the policy. Reinforcementlearning is to get best V(s), not R(s).
the objective:
Find a policy π(S) that max thefunction: E[ ]->max
Discount factor
Value function: (s)
Planning = calculate value functions
Howto compute this functions max?
Use value iteration to get optimal policies.
Everystate s, Vk(s) is finding an action that max the value of Vk(s)using the above function.