斯坦福大学公开课 ：机器学习课程（Andrew Ng）——9、无监督学习：K-means Clustering Algorithm

1）K-means聚类算法（K-means Clustering Algorithm）描述

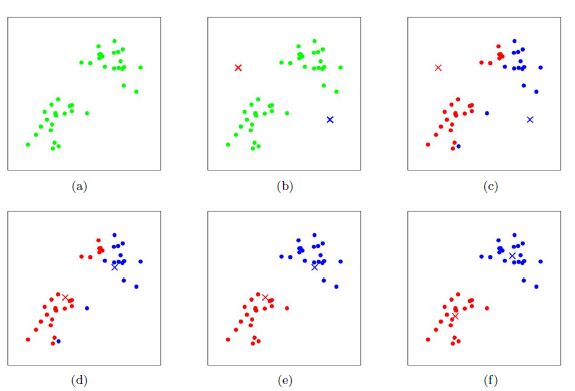
2）2-means聚类算法（K-means Clustering Algorithm）效果展示图片

3）k-means聚类算法（K-means Clustering Algorithm）收敛性简述

4）支持k-means聚类算法（K-means Clustering Algorithm）有效性的EM思想

K-means Clustering Algorithm是聚类算法中最简单的一种了，但却是非常有效的一种。由于简单，算法描述会一笔带过；由于有效，我们将探讨支持该算法有效性的EM思想。

开始前说一下什么是无监督学习（Unsupervised Learning）：即，训练样本只给出特征值，其中每个，而没有给出对应的y。回忆前面的有监督学习，例如回归、朴素贝叶斯、SVM等，训练样本都是有类别标签y。

1）K-means聚类算法（K-means Clustering Algorithm）描述

K-means算法是将样本聚类成k个簇（cluster），具体算法描述如下：

1、 随机选取k个聚类质心点（cluster centroids）为。 2、 重复下面过程直到收敛 {                对于每一个样例i，计算其应该属于的类                               对于每一个类j，重新计算该类的质心                }

2）2-means聚类算法（K-means Clustering Algorithm）效果展示图片

    

3）k-means聚类算法（K-means Clustering Algorithm）收敛性简述

算法描述中强调算法结束条件就是收敛，下面我们定性的描述一下K-means完全可以保证收敛性。

首先，我们定义畸变函数（distortion function）如下：     ，J函数表示每个样本点到其质心的距离平方和，K-means是要将J调整到最小。

假设当前J没有达到最小值，那么可以固定每个类的质心，调整每个样例的所属的类别来让J函数减少，同样，固定，调整每个类的质心也可以使J减小。这两个过程就是算法描述中的两个内部循环过程。当J递减到最小时，和c也同时收敛。（在理论上，可以有多组不同的和c值能够使得J取得最小值，但这种现象实际上很少见）。

但由于畸变函数J是非凸函数，意味着我们不能保证取得的最小值是全局最小值，也就是说k-means对质心初始位置的选取比较敏感。所以如果怕陷入局部最优，那么可以选取不同的聚类质心点多跑几遍k-means，然后取其中最小的J对应的和c输出。（但每跑一次都计算J并比较，貌似效率不是很高）

4）支持k-means聚类算法（K-means Clustering Algorithm）有效性的EM思想

首先给出EM的思想：E步就是估计隐含变量（这里指类别y）的期望值，M步调整其他参数使得在给定隐含变量（这里指类别y）的情况下，训练样本终极评价标准能够达到最优（一般情况下是指训练样本极大似然估计P(x,y)能够达到极大值）。然后在其他参数确定的情况下，重新估计隐含变量（这里指类别y）的期望值，周而复始，直至收敛。

（不懂E-M思想的话可以先看后面的几篇总结）

上面的阐述有点费解，所以我们回到K-means问题本身，我们目的是将样本分成k个类，其实说白了就是求每个样例x的隐含类别y，然后利用隐含类别将x归类。我们一开始不知道每个样例对应隐含变量（这里指类别y，也就是最佳类别），所以最开始随便指定一个给它，然后为了让P(x,y)最大（这里要让机变函数J最小），我们求出在给定c情况下，J最小时的（前面提到的其他未知参数）；当确定后，我们发现可以有更好的（质心与样例距离最小的类别）指定给样例，那么得到重新调整，上述过程周而复始，直到没有更好的指定。这样从K-means里我们可以看出它其实就是EM的体现，E步是确定的最佳隐含类别，M步更新其他参数来使J最小化。只不过这里的隐含类别变量指定方法比较特殊，属于硬指定，从k个类别中“硬性”选出一个给样例，而不是对每个类别赋予不同的概率进而根据概率选择。

参考：http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006910.html