HDU 5441 Travel(离线 + 带权并查集)——2015 ACM/ICPC Asia Regional Changchun Online
Travel
Time Limit: 1500/1000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others)
Problem Description
Jack likes to travel around the world, but he doesn’t like to wait. Now, he is traveling in the Undirected Kingdom. There are
n cities and
m bidirectional roads connecting the cities. Jack hates waiting too long on the bus, but he can rest at every city. Jack can only stand staying on the bus for a limited time and will go berserk after that. Assuming you know the time it takes to go from one city to another and that the time Jack can stand staying on a bus is
x minutes, how many pairs of city
(a,b) are there that Jack can travel from city
a to
b without going berserk?
Input
The first line contains one integer
T,T≤5 , which represents the number of test case.
For each test case, the first line consists of three integers n,m and q where n≤20000,m≤100000,q≤5000 . The Undirected Kingdom has n cities and m bidirectional roads, and there are q queries.
Each of the following m lines consists of three integers a,b and d where a,b∈{1,...,n} and d≤100000 . It takes Jack d minutes to travel from city a to city b and vice versa.
Then q lines follow. Each of them is a query consisting of an integer x where x is the time limit before Jack goes berserk.
For each test case, the first line consists of three integers n,m and q where n≤20000,m≤100000,q≤5000 . The Undirected Kingdom has n cities and m bidirectional roads, and there are q queries.
Each of the following m lines consists of three integers a,b and d where a,b∈{1,...,n} and d≤100000 . It takes Jack d minutes to travel from city a to city b and vice versa.
Then q lines follow. Each of them is a query consisting of an integer x where x is the time limit before Jack goes berserk.
Output
You should print
q lines for each test case. Each of them contains one integer as the number of pair of cities
(a,b) which Jack may travel from
a to
b within the time limit
x .
Note that (a,b) and (b,a) are counted as different pairs and a and b must be different cities.
Note that (a,b) and (b,a) are counted as different pairs and a and b must be different cities.
Sample Input
1 5 5 3 2 3 6334 1 5 15724 3 5 5705 4 3 12382 1 3 21726 6000 10000 13000
Sample Output
2 6 12
Source
2015 ACM/ICPC Asia Regional Changchun Online
题意:给你一个带权的无向图,然后q(q≤5000)次询问,问有多少对城市(城市对(u,v)与(v,u)算不同的城市对,而且u≠v)之间的边的长度不超过d(如果城市u到城市v途经城市w,那么需要城市u到城市w的长度e1≤d,同时城市w到城市v的长度e2≤d)
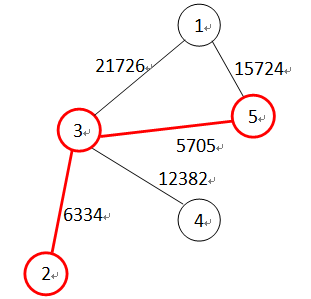
为了方便理解,我们拿样例举例按照样例,我们可以得到上面这样的无向图,对于第二个询问,x=10000,那么满足条件的边有2<->3、3<->5
那么满足条件的城市对有6对,分别为(2,3),(3,2),(3,5),(5,3),(2,5),(5,2)
通过这一点,我们可以发现,对于各个连通块,该连通块(连通块的意思是满足条件的城市形成的连通分支)内城市的个数就决定了城市对的对数,就比如上面这个例子,仅有一个连通块,连通块内有3个城市,那么城市对的对数即为3*(3-1),那样的话,我们只需用并查集计算出连通块的个数以及各个连通块内的城市数,求和即为所求
另外,需要提及的一点是,若每次询问,我们都从头建立并查集的话,时间复杂度是O(m*q)=O(500000000),显然会超时,所以采取离线的方法,将询问按照x从小到大排序之后一次性计算出来,这样,每次只需在前一次询问的基础上扩充并查集就可以了,时间复杂度会减少很多,是O(m)的吧
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<stdlib.h>
#include<cmath>
#include<string>
#include<algorithm>
#include<iostream>
#define exp 1e-10
using namespace std;
const int N = 5005;
const int inf = 1000000000;
const int mod = 2009;
struct edge
{
int a,b,d;
}e[20*N];
bool cmp1(edge x,edge y)
{
return x.d<y.d;
}
struct berserk
{
int v,id;
}x[N];
bool cmp2(berserk x,berserk y)
{
return x.v<y.v;
}
int s[4*N],w[4*N],ans[N];
int fun(int x)
{
if(s[x]!=x)
s[x]=fun(s[x]);
return s[x];
}
int main()
{
int t,n,m,q,i,j,a,b,d,c,u,v;
scanf("%d",&t);
while(t--)
{
scanf("%d%d%d",&n,&m,&q);
for(i=1;i<=n;i++)
s[i]=i,w[i]=1;
for(i=0;i<m;i++)
scanf("%d%d%d",&e[i].a,&e[i].b,&e[i].d);
sort(e,e+m,cmp1);
for(i=0;i<q;i++)
{
scanf("%d",&x[i].v);
x[i].id=i;
}
sort(x,x+q,cmp2);
for(i=j=c=0;i<q;i++)
{
for(;j<m&&e[j].d<=x[i].v;j++)
{
u=fun(e[j].a);
v=fun(e[j].b);
if(u!=v)
{
c-=w[u]*(w[u]-1)+w[v]*(w[v]-1);
w[v]+=w[u];
w[u]=0;
c+=w[v]*(w[v]-1);
s[u]=v;
}
}
ans[x[i].id]=c;
}
for(i=0;i<q;i++)
printf("%d\n",ans[i]);
}
return 0;
}
菜鸟成长记