POJ 3133 Manhattan Wiring 解题报告(插头DP)
| Time Limit: 5000MS | Memory Limit: 65536K | |
| Total Submissions: 1358 | Accepted: 795 |
Description
There is a rectangular area containing n × m cells. Two cells are marked with “2”, and another two with “3”. Some cells are occupied by obstacles. You should connect the two “2”s and also the two “3”s with non-intersecting lines. Lines can run only vertically or horizontally connecting centers of cells without obstacles.
Lines cannot run on a cell with an obstacle. Only one line can run on a cell at most once. Hence, a line cannot intersect with the other line, nor with itself. Under these constraints, the total length of the two lines should be minimized. The length of a line is defined as the number of cell borders it passes. In particular, a line connecting cells sharing their border has length 1.
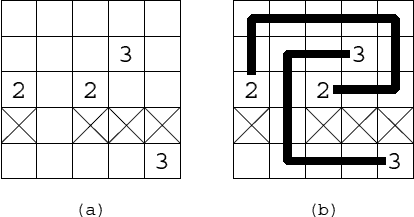
Fig. 1(a) shows an example setting. Fig. 1(b) shows two lines satisfying the constraints above with minimum total length 18.
Figure 1: An example of setting and its solution
Input
The input consists of multiple datasets, each in the following format.
n m row1 … rown
n is the number of rows which satisfies 2 ≤ n ≤ 9. m is the number of columns which satisfies 2 ≤ m ≤ 9. Each rowi is a sequence of m digits separated by a space. The digits mean the following.
0:Empty
1:Occupied by an obstacle
2:Marked with “2”
3:Marked with “3”
The end of the input is indicated with a line containing two zeros separated by a space.
Output
Sample Input
5 5 0 0 0 0 0 0 0 0 3 0 2 0 2 0 0 1 0 1 1 1 0 0 0 0 3 2 3 2 2 0 0 3 3 6 5 2 0 0 0 0 0 3 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 2 3 0 5 9 0 0 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 2 0 0 0 0 0 2 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 9 9 3 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 3 9 9 0 0 0 1 0 0 0 0 0 0 2 0 1 0 0 0 0 3 0 0 0 1 0 0 0 0 2 0 0 0 1 0 0 0 0 3 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 9 9 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 3 2 0 0
Sample Output
18 2 17 12 0 52 43
解题报告:思考了挺久,第一次敲是这么做的。使用8进制。0表示无插头,1表示线路的左插头,2表示线路的有插头。3表示地图上标记为2的点形成的插头,4表示地图上标记为3的点形成的插头。写了大段的状态转移,最后战战兢兢的提交了,4K代码竟然1A了= =。第一次提交代码如下:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=100013;
int now,pre;
int maze[10][10];
struct Node
{
int H[maxn];
int N[maxn];
int S[maxn];
int size;
void init()
{
size=0;
memset(H,-1,sizeof(H));
}
void push(int SS,int num)
{
int s=SS%maxn;
while( ~H[s] && S[H[s]]!=SS )
s=(s+1)%maxn;
if( ~H[s] )
{
N[H[s]]=min(N[H[s]],num);
return ;
}
N[size]=num;
S[size]=SS;
H[s]=size++;
}
int get(int SS)
{
int s=SS%maxn;
while( ~H[s] && S[H[s]]!=SS )
s=(s+1)%maxn;
if( ~H[s] )
return N[H[s]];
return 2;
}
} dp[2];
int get(int S,int p,int l=3)
{
return (S>>(p*l))&((1<<l)-1);
}
void set(int &S,int p,int v,int l=3)
{
S^=get(S,p,l)<<(p*l);
S^=v<<(p*l);
}
int main()
{
int n,m;
while( scanf("%d%d",&n,&m),n||m )
{
for(int i=0;i<=n;i++) for(int j=0;j<=m;j++)
maze[i][j]=1;
for(int i=0;i<n;i++) for(int j=0;j<m;j++)
scanf("%d",&maze[i][j]);
now=0;
pre=1;
dp[now].init();
dp[now].push(0,0);
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
swap(now,pre);
dp[now].init();
for(int s=0;s<dp[pre].size;s++)
{
int S=dp[pre].S[s];
int num=dp[pre].N[s];
int p=get(S,j);
int q=get(S,j+1);
if(maze[i][j]==1)
{
if(p==0 && q==0)
{
dp[now].push(S,num);
}
continue;
}
if(maze[i][j]>=2)
{
int no=maze[i][j]+1;
if((p==no && q==0)||(q==no && p==0))
{
set(S,j,0);
set(S,j+1,0);
dp[now].push(S,num+1);
}
else if(p==0 && q==0)
{
if(maze[i+1][j]!=1)
{
set(S,j,no);
dp[now].push(S,num+1);
}
if(maze[i][j+1]!=1)
{
set(S,j,0);
set(S,j+1,no);
dp[now].push(S,num+1);
}
}
else if((p==0)^(q==0))
{
if(max(p,q)==1)
{
int find=1;
for(int k=j+2;k<=m;k++)
{
int v=get(S,k);
if(v==2) find--;
else if(v==1) find++;
if(find==0)
{
set(S,j,0);
set(S,j+1,0);
set(S,k,no);
dp[now].push(S,num+1);
break;
}
}
}
else if(max(p,q)==2)
{
int find=1;
for(int k=j-1;k>=0;k--)
{
int v=get(S,k);
if(v==2) find++;
else if(v==1) find--;
if(find==0)
{
set(S,j,0);
set(S,j+1,0);
set(S,k,no);
dp[now].push(S,num+1);
break;
}
}
}
}
continue;
}
if(p==0 && q==0)
{
dp[now].push(S,num);
if(maze[i][j+1]!=1 && maze[i+1][j]!=1)
{
set(S,j,1);
set(S,j+1,2);
dp[now].push(S,num+1);
}
}
else if((p>0)^(q>0))
{
if(maze[i+(p>0)][j+(q>0)]!=1)
dp[now].push(S,num+1);
set(S,j,q);
set(S,j+1,p);
if(maze[i+(q>0)][j+(p>0)]!=1)
dp[now].push(S,num+1);
}
else if((p>=3 && p==q)||(p==2 && q==1))
{
set(S,j,0);
set(S,j+1,0);
dp[now].push(S,num+1);
}
else if(p==1 && q==1)
{
int find=1;
for(int k=j+2;k<=m;k++)
{
int v=get(S,k);
if(v==1) find++;
else if(v==2) find--;
if(find==0)
{
set(S,j,0);
set(S,j+1,0);
set(S,k,1);
dp[now].push(S,num+1);
break;
}
}
}
else if(p==2 && q==2)
{
int find=1;
for(int k=j-1;k>=0;k--)
{
int v=get(S,k);
if(v==2) find++;
else if(v==1) find--;
if(find==0)
{
set(S,j,0);
set(S,j+1,0);
set(S,k,2);
dp[now].push(S,num+1);
break;
}
}
}
else if(max(p,q)>=3 && min(p,q)==1)
{
int find=1;
for(int k=j+2;k<=m;k++)
{
int v=get(S,k);
if(v==2) find--;
else if(v==1) find++;
if(find==0)
{
set(S,j,0);
set(S,j+1,0);
set(S,k,max(p,q));
dp[now].push(S,num+1);
break;
}
}
}
else if(max(p,q)>=3 && min(p,q)==2)
{
int find=1;
for(int k=j-1;k>=0;k--)
{
int v=get(S,k);
if(v==1) find--;
else if(v==2) find++;
if(find==0)
{
set(S,j,0);
set(S,j+1,0);
set(S,k,max(p,q));
dp[now].push(S,num+1);
break;
}
}
}
else
{
}
}
}
for(int s=0;s<dp[now].size;s++)
dp[now].S[s]<<=3;
}
printf("%d\n",dp[now].get(0)-2);
}
} 后来优化了下,将maxn该成29989,直接204MS搞定,排名第7哈哈。没有往下试了,有兴趣的可以继续。
看了下kuangbin大神的思路,直接用2表示2号插头,3表示3号插头。之前不敢这么做是因为担心产生回路,现在想一下,整个过程都在贪心,肯定不会有回路嘛。改了下代码,如下:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=59999;
int now,pre;
int maze[10][10];
struct Node
{
int H[maxn];
int N[maxn];
int S[maxn];
int size;
void init()
{
size=0;
memset(H,-1,sizeof(H));
}
void push(int SS,int num)
{
int s=SS%maxn;
while( ~H[s] && S[H[s]]!=SS )
s=(s+1)%maxn;
if( ~H[s] )
{
N[H[s]]=min(N[H[s]],num);
return ;
}
N[size]=num;
S[size]=SS;
H[s]=size++;
}
int get(int SS)
{
int s=SS%maxn;
while( ~H[s] && S[H[s]]!=SS )
s=(s+1)%maxn;
if( ~H[s] )
return N[H[s]];
return 2;
}
} dp[2];
int L=2;
int get(int S,int p)
{
return (S>>(p*L))&((1<<L)-1);
}
void set(int &S,int p,int v)
{
S^=get(S,p)<<(p*L);
S^=v<<(p*L);
}
int main()
{
int n,m;
while( scanf("%d%d",&n,&m),n||m )
{
memset(maze,0,sizeof(maze));
for(int i=0;i<n;i++) for(int j=0;j<m;j++)
{
scanf("%d",&maze[i][j]);
if(maze[i][j]<=1) maze[i][j]^=1;
}
now=0;
pre=1;
dp[now].init();
dp[now].push(0,0);
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
swap(now,pre);
dp[now].init();
for(int s=0;s<dp[pre].size;s++)
{
int S=dp[pre].S[s];
int num=dp[pre].N[s];
int p=get(S,j);
int q=get(S,j+1);
if(maze[i][j]==0)
{
if(p==0 && q==0)
dp[now].push(S,num);
continue;
}
if(maze[i][j]>=2)
{
if((p>0)^(q>0))
{
if(max(p,q)==maze[i][j])
{
set(S,j,0);
set(S,j+1,0);
dp[now].push(S,num+1);
}
}
if(p==0 && q==0)
{
if(maze[i+1][j])
{
set(S,j,maze[i][j]);
set(S,j+1,0);
dp[now].push(S,num+1);
}
if(maze[i][j+1])
{
set(S,j,0);
set(S,j+1,maze[i][j]);
dp[now].push(S,num+1);
}
}
continue;
}
if(p==0 && q==0)
{
dp[now].push(S,num);
if(maze[i+1][j] && maze[i][j+1])
{
set(S,j,2);
set(S,j+1,2);
dp[now].push(S,num+1);
set(S,j,3);
set(S,j+1,3);
dp[now].push(S,num+1);
}
}
else if((p>0) ^ (q>0))
{
if(maze[i+(p>0)][j+(q>0)])
dp[now].push(S,num+1);
set(S,j,q);
set(S,j+1,p);
if(maze[i+(q>0)][j+(p>0)])
dp[now].push(S,num+1);
}
else if(p==q)
{
set(S,j,0);
set(S,j+1,0);
dp[now].push(S,num+1);
}
}
}
for(int s=0;s<dp[now].size;s++)
dp[now].S[s]<<=L;
}
printf("%d\n",dp[now].get(0)-2);
}
}
这段代码时间挺长,也没有再优化了。
越是长的代码越是担心。如果真的比赛,应该会选择第二种吧,思路代码都清晰。
最小表示法:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int maxn=59999;
const int L=2;
int now,pre;
int n,m;
int endx,endy;
int maze[15][15];
int code[15];
struct Node
{
int h[maxn];
int n[maxn];
LL s[maxn];
int size;
void init()
{
memset(h,-1,sizeof(h));
size=0;
}
void push(LL ss,int num)
{
int i=ss%maxn;
while( ~h[i] && s[h[i]]!=ss )
i=(i+1)%maxn;
if( ~h[i] )
{
n[h[i]]=min(n[h[i]],num);
}
else
{
s[size]=ss;
n[size]=num;
h[i]=size++;
}
}
int get(LL ss)
{
int i=ss%maxn;
while( ~h[i] && s[h[i]]!=ss )
i=(i+1)%maxn;
if( ~h[i] )
return n[h[i]]-2;
else
return 0;
}
} dp[2];
void decode(LL s)
{
for(int i=0;i<=m;i++)
code[i]=s&((1<<L)-1),s>>=L;
}
LL encode()
{
LL s=0;
for(int i=m;i>=0;i--)
{
s<<=L;
s|=code[i];
}
return s;
}
void shift()
{
for(int s=0;s<dp[now].size;s++)
dp[now].s[s]<<=L;
}
void merge(int a,int b)
{
for(int i=0;i<=m;i++) if(code[i]==a)
code[i]=b;
}
void doGrid(int i,int j)
{
for(int s=0;s<dp[pre].size;s++)
{
decode(dp[pre].s[s]);
int num=dp[pre].n[s];
int left=code[j];
int up=code[j+1];
int ma=max(left,up);
int mi=min(left,up);
int val=maze[i][j];
if(val==0)
{
if(ma==0)
dp[now].push(encode(),num);
continue;
}
else if(val>1)
{
if(ma==val && mi==0)
{
code[j]=0;
code[j+1]=0;
dp[now].push(encode(),num+1);
continue;
}
else if(ma==0)
{
if(maze[i+1][j]==1 || maze[i+1][j]==val)
{
code[j]=val;
code[j+1]=0;
dp[now].push(encode(),num+1);
}
if(maze[i][j+1]==1 || maze[i][j+1]==val)
{
code[j]=0;
code[j+1]=val;
dp[now].push(encode(),num+1);
}
}
continue;
}
if(ma==0)
{
dp[now].push(encode(),num);
if(maze[i][j+1] && maze[i+1][j])
{
code[j]=code[j+1]=2;
dp[now].push(encode(),num+1);
code[j]=code[j+1]=3;
dp[now].push(encode(),num+1);
}
}
else if(mi==0)
{
if(maze[i+1][j]==1 || maze[i+1][j]==ma)
{
code[j]=ma;
code[j+1]=0;
dp[now].push(encode(),num+1);
}
if(maze[i][j+1]==1 || maze[i][j+1]==ma)
{
code[j]=0;
code[j+1]=ma;
dp[now].push(encode(),num+1);
}
}
else if(left==up)
{
code[j]=code[j+1]=0;
dp[now].push(encode(),num+1);
}
}
}
void solve()
{
now=1,pre=0;
dp[now].init();
dp[now].push(0,0);
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
swap(now,pre);
dp[now].init();
doGrid(i,j);
}
shift();
}
}
void init()
{
memset(maze,0,sizeof(maze));
for(int i=0;i<n;i++) for(int j=0;j<m;j++)
{
scanf("%d",&maze[i][j]);
if(maze[i][j]<=1) maze[i][j]^=1;
}
}
int main()
{
int cas=1;
while(scanf("%d%d",&n,&m),n||m)
{
init();
solve();
printf("%d\n",dp[now].get(0));
}
}