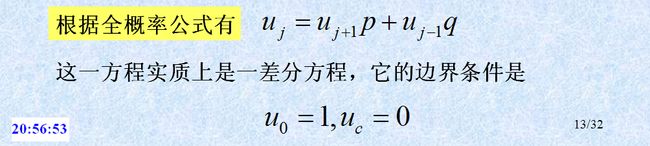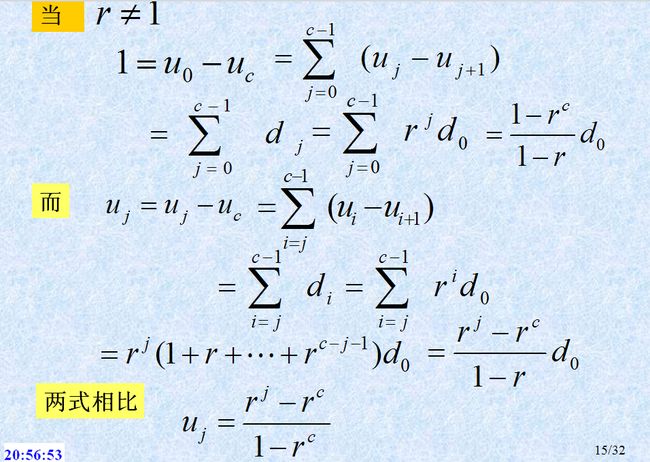hdu 1204 糖果大战 概率（Markov过程）

题意：

两人比赛（定义成甲和乙），两人一开始分别有n和m个糖果，玩24点，每赢一局从对方那里获得一个糖果，谁先没有糖果谁输。两个人能解除24点的概率分别为a和b，若都解出或都没解出则为平局，不交换糖果。求甲赢的概率。

题解：

一个Markov过程的应用。详细信息链接：Markov过程-百度文库

具体Markov过程没有怎么了解，基本概念是马可夫过程的条件概率仅仅与系统的当前状态相关，而与它的过去历史或未来状态，都是独立、不相关的。

这题相当于赌徒问题的变形（只是加了平局）。

具体过程：

设0<=j<=n+m；uj为从j个糖果到达0个糖果状态先于到达n+m个糖果状态的概率。

那么uj=p*u(j+1)+q*u(j-1)+(1-p-q)*uj（p为甲胜的概率，q为乙胜的概率，这个公式的意思是j状态可以转到的状态）

(p+q)uj=p*u(j+1)+q*u(j-1)化简后即跟赌徒问题一样了。（其中p=a*(1-b),q=b*(1-a)）

之后的情况见下图：

赌徒输光问题：

代码：

#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <ctime>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <map>
#include <set>
#include <vector>
#include <queue>
#include <iomanip>
using namespace std;

const double eps=1e-12;
int main()
{
    int n,m;
    double p,q;
    while(scanf("%d%d%lf%lf",&n,&m,&p,&q)!=EOF)
    {
        double ans,r;
        if(m==0)ans=1;//如果m=0，那么即使n=0也会赢
        else if(n==0||p==0||q==1)ans=0;
        else
        {
            r=q*(1-p)/(p*(1-q));//Speakless胜的概率p*(1-q)
            if(fabs(r-1.0)<eps)ans=1.0*n/(n+m);//胜率相等
            else ans=(1-pow(r,n))/(1-pow(r,n+m));
        }
        printf("%.2f\n",ans);
    }
    return 0;
}
/*
Markov过程（马尔科夫过程）
*/