正弦函数及其FFT变换(二)

        FFT变换，其实就是快速离散傅里叶变换，傅立叶变换是数字信号处理领域一种很重要的算法。要知道傅立叶变换算法的意义，首先要了解傅立叶原理的意义。傅立叶原理表明：任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。而根据该原理创立的傅立叶变换算法利用直接测量到的原始信号，以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位。

        和傅立叶变换算法对应的是反傅立叶变换算法。该反变换从本质上说也是一种累加处理，这样就可以将单独改变的正弦波信号转换成一个信号。因此，可以说，傅立叶变换将原来难以处理的时域信号转换成了易于分析的频域信号（信号的频谱），可以利用一些工具对这些频域信号进行处理、加工。最后还可以利用傅立叶反变换将这些频域信号转换成时域信号。

        一个模拟信号，经过ADC采样之后，就变成了数字信号。 采样得到的数字信号，就可以做FFT变换了。N个采样点，经过FFT之后，就可以得到N个点的FFT结果。为了方便进行FFT运算，通常N取2的整数次方。
        假设采样频率为Fs，信号频率F，采样点数为N。那么FFT之后结果就是一个为N点的复数。每一个点就对应着一个频率点。这个点的模值，就是该频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢？假设原始信号的峰值为A，那么FFT的结果的每个点（除了第一个点直流分量之外）的模值就是A的N/2倍。而第一个点就是直流分量，它的模值就是直流分量的N倍。而每个点的相位呢，就是在该频率下的信号的相位。第一个点表示直流分量（即0Hz），而最后一个点N的再下一个点（实际上这个点是不存在的，这里是假设的第N+1个点，也可以看做是将第一个点分做两半分，另一半移到最后）则表示采样频率Fs，这中间被N-1个点平均分成N等份，每个点的频率依次增加。由此可见，FFT频谱图中所能达到的分辨率为为Fs/N，即某点n所表示的频率为：Fn=(n-1)*Fs/N。如果采样频率Fs为1024Hz，采样点数为1024点，则可以分辨到1Hz。

        假设FFT之后某点n用复数a+bi表示，那么这个复数的模就是An=sqrt（a*a+b*b）（某点处的幅度值An = A*(N/2)），相位就是Φ=atan2(b,a)。根据以上的结果，就可以计算出n点（n≠1，且n<=N/2）对应的信号的表达式为：2*An/N*cos(2*pi*Fn*t+Φ)。对于n=1点的信号，是直流分量，幅度即为A1/N。由于FFT结果的对称性，通常我们只使用前半部分的结果，即小于采样频率一半的结果。
        下面以上一篇文章的信号来做说明

f0=10;fs=80;N=64;n=0:N-1;y=sin(2*pi*n*f0/fs);则matlab程序为

f0=10;
fs=80;
N=64;
n=0:N-1;
y=sin(2*pi*n*f0/fs);
y1=fft(y);
z=abs(y1);
plot(n,z);
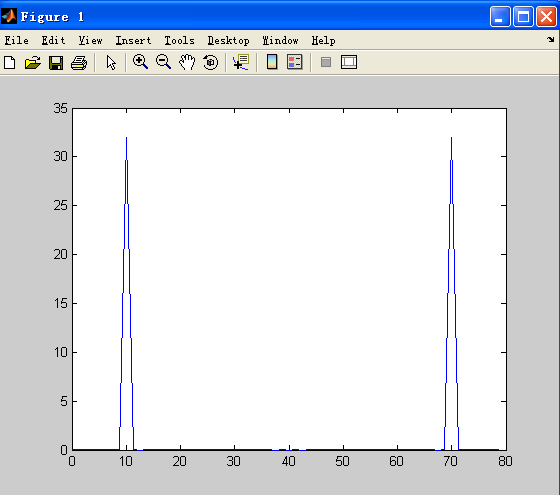
 图形为：

 由图形可知 在n = 8时有最大值32，可以验证上述是否成立，并且验证x[n]是否与x[t]有对应关系。

因为An = A*(N/2)，所以A = 1

因为频谱分辨率为fs/N = 1.25，所以fs = n*fs/N = 8*1.25 = 10，与原函数相同

如果想在图形中直接显示原函数的频率需要将n轴归一化