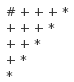从《编程之美》买票找零问题说起,娓娓道来卡特兰数——兼爬坑指南
从《编程之美》买票找零问题说起,娓娓道来卡特兰数——兼爬坑指南
引子:
大约两个月前,我在练习一些招聘的笔试题中,有一道和卡特兰数相关。那时还没来得及开始仔细看《编程之美》,就先翻到那一章节,草草地看了下买票找零的例子和证明并把书上的![]() 背下来了事。当然,只靠这个式子是可以解决一些问题的,但不知是《编程之美》的作者有意挖的陷阱来甄别所谓的“Poser”,还是疏忽了没有进一步讨论,又或者是因限于篇幅而将更本质的东西留给感兴趣的读者来挖掘,对于能用一般卡特兰数解决的问题,这个特殊的式子是解决不了的。当然,做为一本上市了很多年的书,《编程之美》上的各个问题在网络上都能找到相关的讨论和文章,更不用说卡特兰数——自发现至今已有200年左右——的相关资料更是比比皆是。因此,本文的主要目的不是向读者再一次地介绍卡特兰数的性质和应用,而是帮助读者跨越《编程之美》留下的陷阱,找寻更一般化的卡特兰数的公式,从而解决更一般的问题。
背下来了事。当然,只靠这个式子是可以解决一些问题的,但不知是《编程之美》的作者有意挖的陷阱来甄别所谓的“Poser”,还是疏忽了没有进一步讨论,又或者是因限于篇幅而将更本质的东西留给感兴趣的读者来挖掘,对于能用一般卡特兰数解决的问题,这个特殊的式子是解决不了的。当然,做为一本上市了很多年的书,《编程之美》上的各个问题在网络上都能找到相关的讨论和文章,更不用说卡特兰数——自发现至今已有200年左右——的相关资料更是比比皆是。因此,本文的主要目的不是向读者再一次地介绍卡特兰数的性质和应用,而是帮助读者跨越《编程之美》留下的陷阱,找寻更一般化的卡特兰数的公式,从而解决更一般的问题。
内容提要(点击跳转;博文右下角的回到顶部的链接,可回到本页):
- 阅读建议(请先看这里!)
- 《编程之美》的卡特兰数
- 问题引入和分析
- 非正式的证明
- 母函数法证明
- 扩展问题
- 入栈出栈问题
- 矩阵连乘问题
- 街区对角线问题
- 圆上点对互连问题
- 一般的卡特兰数
- “狭隘”的卡特兰数不适用于多边形划分问题、(非满/满)二叉树构造问题
- 一般的卡特兰数推导方式并解决多边形划分问题、(非满/满)二叉树构造问题
- n层阶梯分割问题和引申
- 填数问题/照相问题
- 程序实现
- 公式法
- 递推法
- 两种算法比较
- 参考资料
阅读建议:
- 读过《编程之美》?正如引子提到的,本文希望能使掉到《编程之美》的陷阱里的读者能够顺利爬坑。如果你没掉坑里,恭喜你,我们可以一起交流下这个坑是什么样的。不过对于街区不跨越对角线问题,不知道你是否与我一样多想了一点东西?
- 没读过《编程之美》?那么你只需提高警惕,文中会告诉你坑在哪里,而不是让你先跳下去再爬出来。
- 没有学习过母函数是什么和怎么使用?那么用母函数证明的过程就不必太在意了,其实用数学归纳法也可以证明。我把证明写在上面的主要原因是增强读者的信心:这些东西并不是凭空而来。
- 之前读过卡特兰数,想直接做练习?没关系,如果做题的过程中发现自己理解有问题可以再去文中相应的解释去看嘛。
- 想直接了解如何编程解决?没问题,最后有两段很好理解的代码,捎带进行了分析。
[回到索引 或继续阅读]
《编程之美》的卡特兰数
先简单概括一下《编程之美》是如何引入和介绍卡特兰数的。
问题(《编程之美》4.3买票找零):2n个人排队买票,其中n个人持50元,n个人持100元。每张票50元,且一人只买一张票。初始时售票处没有零钱找零。请问这2n个人一共有多少种排队顺序,不至于使售票处找不开钱?
分析1:队伍的序号标为0,1,...,2n-1,并把50元看作左括号,100元看作右括号,合法序列即括号能完成配对的序列。对于一个合法的序列,第0个一定是左括号,它必然与某个右括号配对,记其位置为k。那么从1到k-1、k+1到2n-1也分别是两个合法序列。那么,k必然是奇数(1到k-1一共有偶数个),设k=2i+1。那么剩余括号的合法序列数为f(2i)*f(2n-2i-2)个。取i=0到n-1累加,
并且令f(0)=1,再由组合数C(0,0)=0,可得
至于怎么推导,《编程之美》就没有详细地说明,而是用另一个角度来解释,这个解释类似于《计算机程序设计艺术(卷一)》2.2.1节习题4的解答提到的精彩解法“反射原理”,下面是对其的概括(我所知的最早的出处是:http://bbs.csdn.net/topics/320099239)
问题大意是用S表示入栈,X表示出栈,那么合法的序列有多少个(S的个数为n)
显然有c(2n, n)个含S,X各n个的序列,剩下的是计算不允许的序列数(它包含正确个数的S和X,但是违背其它条件).
在任何不允许的序列中,定出使得X的个数超过S的个数的第一个X的位置。然后在导致并包括这个X的部分序列中,以S代替所有的X并以X代表所有的S。结果是一个有(n+1)个S和(n-1)个X的序列。反过来,对一垢一种类型的每个序列,我们都能逆转这个过程,而且找出导致它的前一种类型的不允许序列。例如XXSXSSSXXSSS必然来自SSXSXXXXXSSS。这个对应说明,不允许的序列的个数是c(2n, n-1),因此an = c(2n, n) - c(2n, n-1)。
这个解法正好能适用于一种特殊情况,以下是对其的叙述:
n+m个人排队买票,并且满足,票价为50元,其中n个人各手持一张50元钞票,m个人各手持一张100元钞票,除此之外大家身上没有任何其他的钱币,并且初始时候售票窗口没有钱,问有多少种排队的情况数能够让大家都买到票。
这个题目是Catalan数的变形,不考虑人与人的差异,如果m=n的话那么就是我们初始的Catalan数问题,也就是将手持50元的人看成是+1,手持100元的人看成是-1,任前k个数值的和都非负的序列数。
这个题目区别就在于n>m的情况,此时我们仍然可以用原先的证明方法考虑,假设我们要的情况数是![]() ,无法让每个人都买到的情况数是
,无法让每个人都买到的情况数是![]() ,那么就有
,那么就有![]() ,此时我们求
,此时我们求![]() ,我们假设最早买不到票的人编号是k,他手持的是100元并且售票处没有钱,那么将前k个人的钱从50元变成100元,从100元变成50元,这时候就有n+1个人手持50元,m-1个手持100元的,所以就得到,于是我们的结果就因此得到了,表达式是
,我们假设最早买不到票的人编号是k,他手持的是100元并且售票处没有钱,那么将前k个人的钱从50元变成100元,从100元变成50元,这时候就有n+1个人手持50元,m-1个手持100元的,所以就得到,于是我们的结果就因此得到了,表达式是![]() 。
。
(出处:http://daybreakcx.is-programmer.com/posts/17315.html 作者daybreakcx)
为了便于下面的说明,我在这里用母函数方法推导一下。由于公式不便在HTML里排版,我在Word里推导完直接截了个图贴上来。
细心的读者可能发现了陷阱所在:f(2n)这个式子可以求解f(0)、f(2)、f(4)等等所有2n形式的数,但是对f(1)、f(3)等奇数是未定义的。但即使你心中闪过这一道灵感,但你也不确定这个怀疑是否有意义:原题本身已经要求了50元和100元是成对的啊?对于f(2n+1)这种,根本就没必要求解嘛。我曾经也这么怀疑过,也曾试图这样说服自己:记住公式足够了;但当我开始研究延伸的问题时发现,这还不够。
不过在进一步的推导前,先来看看这个“狭义”的形式能解决哪些问题吧。
入栈出栈问题(经典问题):
对于一个无限大的栈,一共n个元素,请问有几种合法的入栈出栈形式?
分析:
直接用f(2n)来求解即可。不过可以注意到,对于买票找零问题,一共是2n个人,排的是人的顺序;对于入栈出栈,是n个元素,2n次操作,排的是操作的顺序。究竟把哪个数代入,不要混淆。
矩阵连乘问题(《编程之美》4.3扩展问题1):
P = a1 * a2 * a3 * ... * an,其中ai是矩阵。根据乘法结合律,不改变矩阵的相互顺序,只用括号表示成对的乘积,试问一共有几种括号化方案?
分析:
n个矩阵需要连乘(n-1)次,因此需要(n-1)对括号。且这里的括号只是为了使矩阵两两结合,而不是单纯为加括号而加括号,像( (a1) * (a2)),这里将两个矩阵分别括起来是不符合要求的。因此这里如果确定了括号的顺序,那么矩阵的结合顺序也会确定,如(()())对应了(( a1* a2) * (a3 * a4))。注意到是(n-1)对括号,即(n-1)个左括号和(n-1)个右括号,那么应该使用f[2(n-1)]来计算。
街区对角线问题(《编程之美》4.3扩展问题2类似题目1):
某个城市的某个居民,每天他须要走过2n个街区去上班(他在其住所以北n个街区和以东n个街区处工作)。如果他不跨越(但可以碰到)从家到办公室的对角线,那么有多少条可能的道路?
分析:
(图片来自维基)
为了不跨越对角线,向东走的步数时刻要大于等于向北走的步数,这些点都是处于对角线以下的。可以看出路线序列由n次向东和n次向北组成,且从第一个元素开始的任意子序列中向东次数不少于向北次数。因此方法一共是f(2n)种。
等等,似乎有什么不对。对于网络上我所见过的解答,都是到此为止;但我觉得这里有个陷阱。如果要求不跨越,并且初始点就在对角线上,这明显是个边界条件,完全可以只走上面一半,不违反“不跨越对角线”的要求,即向北走的步数时刻大于等于向东走的步数,那么真实的解应该是2*f(2n)。当然,如果这个问题真出现在面试中了,你可以和面试官探讨一下,问问这么走是否合法?注意边界条件,应该会为面试加分。
圆上点对互连问题(《编程之美》4.3扩展问题2类似题目1):
在圆上选择2n个点,将这些点成对连接起来,且所得n条线段不相交,求可行的方法数。
分析:
乍一看不能像上面三道题那样直接套公式。那么,先进行一下分析,将圆上的点依次标为P0,P1,...P2n-1。为了避免混淆,使用F(2n)表示2n个点可连成的线段数,选择Pk与P0相连(0<k<n),同样地可以看出,k必为奇数,否则1至k-1之间有奇数个点,不可能成对连成直线。同样地把k设为2i+1,那么线段P0Pk把剩余的点分为了1...2i和2i+2...2n-1,且新的连线不能与0k相交,它们只能属于0k把园划分出的这两个区域之一。即F(2n) = ∑F(2i)*F(2n-1-(2i+2)+1) = ∑F(2i)*F(2n-2i-2),其中i = 0 ... n-1。这时,又转化成熟悉的形式了。
但是,这道题还是和上面几道有些区别。前几道题你总是能区分哪些元素/操作是一类,其余的是另一类;而这个问题你如何区分这些看上去是一模一样的2n个点呢?怕是只有从分析入手、发现了其递推公式与卡特兰数的联系,从而才敢使用的吧?什么,直接看到2n就套用公式?再或者,根据2n这个特征,想出这么一种解释:2n个点连成线段,那么把这n个线段看作有方向的,起点和终点各有n个,线段从起点出发,到达终点;为了使线段之间互不交叉,那么任意两个尾点和首点之间必然有等量的首点和尾点,这样还真的又可以套公式了。这么解释当然是可以的,但是显然不如上面几道题那么直观了,而下面的问题你就不能这么解决了,这就是我所谓的《编程之美》挖的坑。(当然也有可能它的解释太过于抽象以至于我没想到,有兴趣的读者可以试试用上面的解释方法尝试解释下面两个问题套用公式的原因)
一般的卡特兰数
多边形划分问题(《编程之美》4.3扩展问题2):
将多边形划分为三角形问题。求一个凸多边形区域划分成三角形区域的方法数。
二叉树构造问题(《编程之美》4.3扩展问题3):
n个结点可构造多少个不同的二叉树。(结点之间没有区别)
怎么样,这里n就不一定是偶数,还敢直接生搬硬套上面的公式么?当然,这里要吐槽下《编程之美》这里令人蛋疼的地方:明明扩展问题2的类似题目1和2比它本身简单,后两题可以直接套用正文的公式而原题要稍费点心思,却要这么组织习题的编排顺序,真是别有用心。
为了解决更一般的问题,满足于f(2n)的计算方法看来是不行了。为与维基上保持一致,下面用Cn来表示卡特兰数,不过我不想直接引入抽象概念,还是从上面两道具体的问题出发吧。
多边形划分问题的分析:
设边数为n,且n>=3,并为顶点依次编号为1,...,n。选定任意一条边作为第一个三角形的边,如P1Pn,此时再为它选择一个顶点k,2<=k<=n-1,此时,n边型被分为了一个k边型(顶点编号由1到k)、一个三角形(顶点编号为1、k、n)、一个n-k+1边型(顶点编号由k到n)。设F2(n)为n边型的划分数,那么
F2(n) = ∑F2(k)F2(n-k+1),其中n>=3,k=2,...,n-2,并且对于三角形可知,F2(3) = 1。F2(n)可表示为:
F2(n) =F2(2)F2(n-1) + F2(3)F2(n-2) + ... + F2(n-2)F2(3) + F2(n-1)F2(2),这个式子看上去已经很通用了,然而对于F2(1)和F2(2)的取值怎么求呢?当然也可以像上面一样先做假设再讨论,但是这里转化一下思路,把问题简化一下。既然讨论所谓的“1边型”、“2边型”其实根本没有意义,“3边型”及以上才有意义,而且3是n的起始值,那么不妨令Cn表示n+2边型的划分数,这样就从C1=1开始,而Cn=F2(n+2)= F2(2)F2(n+1) + F2(3)F2(n) + ... + F2(n)F2(3) + F2(n+1)F2(2),这样就有
Cn=C0Cn-1+C1Cn-2+...+Cn-2C1+Cn-1C0=∑CkCn-k,(n>=1,k=0,...,n-1)
相当于把原先没有意义的情况规避掉了,但是C0依然令人纠结。为了使C1=C0C1也能满足这个公式,只有令C0=1了。用母函数的方法可以求得
是不是与《编程之美》的![]() 很像?可能你会说,“这是因为,在这个问题里有n个顶点和n个边,一个顶点和一条边构成了一个三角形,为了使其能够划分分所有的三角形,顶点数应该大等于边数;对于选定的边,选择一个顶点k后将n边型划分成一个k边型和n-k+1边型,递归地划分”。但可以看到,与前几个问题不同,这种划分方式总是合理的序列,也就是说,这样是在已知总是合法的情况下进行,而不像前几个问题,先判断怎样划分合法,再来划分。当然,这种理解我也不否认,但要挖掘它与前几个问题的联系、搞明白其中的不同,确实要花点心思。如果是为了套用公式而勉强凑出的解释,那下面的问题就更不好办了。同时,Cn的表达式看上去比f(2n)要通用多了,虽然它们其实是一个式子,后者在使用时总是要把代入的2n除以2得到n之后才行,难免遗漏。对于之前分析过的问题,所有用f(2n)的地方都可以用Cn来代替。
很像?可能你会说,“这是因为,在这个问题里有n个顶点和n个边,一个顶点和一条边构成了一个三角形,为了使其能够划分分所有的三角形,顶点数应该大等于边数;对于选定的边,选择一个顶点k后将n边型划分成一个k边型和n-k+1边型,递归地划分”。但可以看到,与前几个问题不同,这种划分方式总是合理的序列,也就是说,这样是在已知总是合法的情况下进行,而不像前几个问题,先判断怎样划分合法,再来划分。当然,这种理解我也不否认,但要挖掘它与前几个问题的联系、搞明白其中的不同,确实要花点心思。如果是为了套用公式而勉强凑出的解释,那下面的问题就更不好办了。同时,Cn的表达式看上去比f(2n)要通用多了,虽然它们其实是一个式子,后者在使用时总是要把代入的2n除以2得到n之后才行,难免遗漏。对于之前分析过的问题,所有用f(2n)的地方都可以用Cn来代替。
进一步地,结合维基,把卡特兰数的递推关系总结为:
这时候解决n个结点的二叉树个数问题就简单了。从递推公式出发,记为F3(n),选出一点为根,k个点作为左子树,n-k-1个点作为右子树。那么F3(n) = ∑F3(k)F3(n-k-1),k=0,...,n-1。容易观察出Cn=F3(n)。这里可以看到,这个问题根本没有必要找出“n个元素和另n个元素成对”这种模式下,这两种元素分别对应问题中的什么东西。
同时,这个问题还可以引申为“2n+1个结点构成的满二叉树个数为Cn个,这是对原题结果中所有二叉树(无论是否为满二叉树)的外结点补上缺失的子结点的结果。
n层阶梯切割问题
解法来自http://blog.csdn.net/duanruibupt/article/details/6869431
n层的阶梯切割为n个矩形的切法数也是![]() 。如下图所示:
。如下图所示:
这个证明是怎么进行的呢?我们先绘制如下的一张图片,即n为5的时候的阶梯:
我们注意到每个切割出来的矩形都必需包括一块标示为*的小正方形,那么我们此时枚举每个*与#标示的两角作为矩形,剩下的两个小阶梯就是我们的两个更小的子问题了,于是我们的![]() 注意到这里的式子就是我们前面的性质3,因此这就是我们所求的结果了。
注意到这里的式子就是我们前面的性质3,因此这就是我们所求的结果了。
我的补充说明:这里的枚举,是分割方法;将原图中枚举的每个以*和#为两角的矩形挖去,将会剩下两个更小的阶梯(或者一个大小为0的阶梯和一个大小非0的阶梯)。同时,从这个途中可以获得启发,此题可以叙述为:4个矩形纸片,大小分别为1*4、2*3、3*2、4*1,把它们摆成上图的阶梯,一共有几种相互覆盖的顺序?(是C4=14种而不是4!=24种,如果想不明白可以用n=3来枚举理解)
填数问题/照相排队问题(阿里、腾讯笔试题)
在一个2*n的格子中填入1到2n这些数值使得每个格子内的数值都比其右边和下边的所有数值都小的情况数;
12个高矮不同的人,排成两排,每排必须是从矮到高排列,而且第二排比对应的第一排的人高,问排列方式有多少种?
分析:
这2n个数选择n个在第一行,剩下的n个在第二行,并且每行都是从小到大排列。比如00001111就对应了1、2、3、4在第一行,5、6、7、8在第二行。为了使第一行比第二行对应位置小,换句话说,要保证序列合法,那么任何从第一个元素的开始的任意子序列中0的个数要大于等于1的个数。这就转化成了Cn。
对于照相问题,n=6,C6 = 132。
(顺便提一下,第一个问题有点像2*n的杨氏矩阵构造问题。对于一般的使用一系列元素构造杨氏矩阵的方法,可以看看http://stackoverflow.com/questions/17501540/all-solutions-for-a-matrix-sorting/17501739#17501739)
程序实现
这一部分来谈谈解题的程序实现。你可能会说,上面的推导都这么详细了,没必要写程序啊?我原先也是这样想的,不外乎先从问题中抽象出待求用的卡特兰数Cn中n的值,然后计算组合数。这里就不管什么什么记忆化优化、递归实现了,就是单纯从定义出发求解,随手写了个函数:
//select m elements from n unsigned long long comb(int n,int m) { unsigned long long res; if((m==0)||(m==n)) res = 1; else { int i; long long numerator=1,denominator=1; if(m>n-m) m = n- m; for(i=1;i<=m;i++) denominator *= i; for(i=0;i<=m-1;i++) numerator *= n-i; res = numerator/denominator; } return res; }
那么,用这个函数计算Cn时,需要进行2n次乘法和2次除法。但是在计算分子的时候,你可能就不放心了:如果溢出怎么办?即使对于long long型,溢出也不是不可能。
现在退而求其次,使用递推公式来求Cn。这里用了一个数组保存上次计算的结果,计算时Cn,不必重新计算前面的C0~Cn-1,从而避免了递归的开销和计算的浪费。下面是完整的程序代码:
#include <stdio.h> #include <stdlib.h> #define MAXN 36 unsigned long long catalan(unsigned long long *array,int n) { static int MaxIndex = -1; if(n<=MaxIndex) return array[n]; if(MaxIndex == -1){ //haven't been initialized. array[0] = 1; MaxIndex = 0; } //for calculating C[n] with C[0],...,C[n-1] //there are C[0],...,C[MaxIndex] while(MaxIndex<n) { int i; MaxIndex++; array[MaxIndex] = 0; for(i=0;i<MaxIndex;i++) array[MaxIndex] += array[i] * array[MaxIndex-1-i]; } return array[MaxIndex]; } int main() { int n; unsigned long long *array; array = malloc((MAXN+1) * sizeof(unsigned long long)); while(1) { scanf("%d",&n); if(n<0) { printf("[error]negative number.\n"); return -1; } else if(n>=MAXN) { printf("[error]larger than 35.\nan unsigned long long can't store it.\n"); return -1; } printf("C%d %lld\n",n,catalan(array,n)); } }
现在对这两个算法进行比较,前者利用组合数计算的算法我称为公式法,后者利用数组保存先前元素、计算所需元素时再按需更新的我称为递推法。它们都没有用到递归。
- 从取值范围来看,递推法要强得多。注释上已经说明了这个程序所能生成的最大卡特兰数的n为35,大于35时,unsigned long long就不能表示了。而用组合数来计算,虽然也是unsigned long long型,但由于多个大整数连续相乘的存在,最大的n只支持14,再大的时候结果就不正确了。假设有某种容器能保存更大的整数,可以把数组也做成动态增长的,随需随扩,而不必预先计算好需要分配的数量,相关的机制就不在这里研究了。
- 从运行速度来看,公式法计算了2n次乘法和2次除法。递推法情况比较复杂,最好情况是计算n时,0...n-1均已生成,那么需要n次乘法和n-1次加法,规模为O(n);最坏情况是前面的都没有生成,规模是O(n2);同时这个算法还可以进一步优化:注意到Cn=C0Cn-1+C1Cn-2+...+Cn-2C1+Cn-1C0=∑CkCn-k(n>=1,k=0,...,n-1)中,求和是左右对称的,也即C0Cn-1=Cn-1C0,这样实际运算时做的乘法数目可以减少一半。这样一来,后者的平均性能应该与前者近似。
- 从适用性来看,公式法只适合卡特兰数计算,而递推法可以用来解决更广泛的问题,比如把Cn=C0Cn-1+C1Cn-2+...+Cn-2C1+Cn-1C0改写成Cn=C0Cn-2+C1Cn-3+...+Cn-3C1+Cn-2C0。这是个我随手写的式子,如果再从头用母函数来推导,费时费力,而且未必有能够简单表示的解。而使用递推法,只需要根据这个递推公式稍微在程序里改一下就能用了,适用性强的不是一点半点。
看来,直接用程序来解决,未必比进行严密地推导得出结论要差。当然,这两种方法能够全面掌握才是最好不过。
后记:
这篇文章大概花了两整天的时间来完成,边写边整理思路。而这篇文章想写已经很久了,有图为证:
![]()
当然,这个草稿里直到这周周一时都仅仅是两个链接而已,中间没怎么关注。写之前没想到会写这么长,不过目前还是比较满意的:对于卡特兰数,从特殊到一般,不拘泥于《编程之美》上的形式,把常见问题都解决了一遍,并用母函数进行推导,而且加上了程序实现。虽然不敢说挖掘了什么新东西,但是把自己原先混乱的思路给好好整理了一下,也顺利从坑中爬出,涨了不少经验,为了便于阅读,本文加了大量锚点和彩色标识,并且尽量用不太枯燥的语言编写,希望读者也能有所收获。
参考资料:
- 《编程之美》4.3:特殊的卡特兰数形式、买票找零问题、矩阵连乘问题、多边形划分三角形问题、街区上班问题、圆上点对互联问题、二叉数构造问题
- 维基百科卡塔兰数:标准的卡特兰数形式、除了以上几种问题外的满二叉树问题、矩形覆盖问题
- 凸多边形的三角形划分解题报告(作者莫名堂堂主):唤起了我对母函数解法的回忆(这篇博文里的推导结果不是维基的标准形式,建议以维基为准)、同时给了我编程解法的启发。
- Catalan数——卡特兰数(作者Hackbuteer1):当初最先看的参考资料,提供了照相问题的解。不过似乎整理自强奸阿里巴巴一个笔试题(楼主baihacker)。对于原帖的NIM问题现在已经理解(最简单的理解在该帖43楼),准备以后总结,不过如果有疑问可以留言给我。
- 《计算机程序设计艺术(卷一)》:其实我只是不想人云亦云而翻书确认了一下Knuth援引的卡特兰数通项的证明方法;以前也曾经说过,这个大部头现在是没时间深入研究了,目前只是作为工具书,用到了就查查而已。
- 小思卡特兰数(作者daybreakcx):矩形覆盖问题以及其他没有解的问题的解,还有把照相排队问题一般化成填数问题的分析、以及n>m时买票找零问题的分析。