R语言之功效分析篇
转载自:http://blog.csdn.net/lilanfeng1991/article/details/33728435
样本大小 :指实验设计中每种条件/组中观测的数目;
显著性水平(alpha):由I型错误的概率来定义,可看做是发现效应不发生的概率;
功效:通过1减去二型错误的概率来定义,即真实效应发生的概率;
效应值:指在重力备择或研究假设下效应的量。
1、用pwr包做功效分析
pwr包中的函数
| 函数 | 功效计算的对象 |
| pwr.2p.test() | 两比例(n相等) |
| pwr.2p2n.test() | 两比例(n不相等) |
| pwr.anova.test() | 平衡的单因素ANOVA |
| pwr.chisq.test() | 卡方检验 |
| pwr.f2.test() | 广义线性模型 |
| pwr.p.test() | 比例(单样本) |
| pwr.r.test() | 相关系数 |
| pwr.t.test() | t检验(单样本、两样本、配对) |
| pwr.t2n.test() | t检验(n不相等的两样本) |
(1)t检验问题一:
反应时间有1.25的偏差,反应时间1s的差值是巨大的差异,可设定要检测的效应值为d=1/1.25=0.8或更大。若差异存在,则希望有90%的把握检测到它,因随机变异性的存在,也希望有95%的把握不会误报差异显著,对于该研究坱要多少受试者呢?
- library(pwr)
- pwr.t.test(d=.8,sig.level=0.05,power=.9,type="two.sample",alternative="two.sided")

每组中需要34个受试者(总共68人),这样才能保证有90%的把握检测到0.8的效应值,并且最多 5%的可能性会误报差异存在。
(2)t检验问题二:
若检测到总体均值0.5个标准差的差异,且将误报差异的几率限制在1%内,另,获得的受试者只有40个,则该研究中,能检测到这么大总体均值差异的概率是多少?
- pwr.t.test(n=20,d=.5,sig.level=.01,type="two.sample",alternative="two.sided")
结果表明,在0.01的先验显著性水平下,每组20个受试者,因变量的标准差为1.25s,有低于14%的可能性断言差值为0.625s或者不显著(d=0.5=0.625/1.25)。换句话说,将有86%的可能性错过要寻找的疚值。即需要慎重考虑要投入到该研究中的时间和精力。
(3)方差分析
eg:
问题:现对五个组做单因素方差分析,要达到0.8的功效,效应值为0.25,并选择0.05的显著性水平,计算各组需要的样本大小
- pwr.anova.test(k=5,f=.25,sig.level=.05,power=.8)

结果表明,总体样本大小为5*39,即195。
(4)相关性
问题:
研究抑郁与孤独的关系
H0:r<=0.25;H1:r>0.25;
- pwr.r.test(r=.25,sig.level=.05,power=.90,alternative="greater")

要满足以上要求,需要134个受试者来评价抑郁与孤独的关系,以便在零假设为候的情况下有90%的信心拒绝它。
(5)线性模型
f^2=R^2/(1-R^2)(1)
f^2=(Rab^2-Ra^2)/(1-Rab^2)(2) (Ra^2表示集合A中变量对总体方差的解释率,Rab^2集合A和B中变量对总体方差的解释率)
当评价一组预测变量对结果的影响程度时,适宜第一个公式来计算f2;
当要评价一组预测变量对结果的影响超过第二组变量时(协变量)多少时,适宜用第二个公式。
问题:
假设想研究老板的领导风格对员工满意度的影响,是否超过薪水和工作小费对员工满意度的影响。领导风格可有讨论会个变量来评估,薪水和小费与三个变量有关。过去的经验表明,薪水和小费能够解释约30%的员工满意度和方差。而从现实出发,领导风格至少能解释35%的方差。假定显著性水平为0.05,则在90%的置信度情况下,坱要多少受试者能够得到这样的方差贡献率?
sig.level=0.05, power=0.90,u=3(总预测变量数送去集合B中的预测变量数),效应值为f2=(0.35-0.30)/(1-0.35)=0.0769
- pwr.f2.test(u=3,f2=0.0769,sig.level=0.05,power=0.90)
多元回归中,分母的自由度等于N-k-1,N是总观测数,k是预测变量数;本例中,N-7-1=185,即需要样本大小N=185+7+1=193
(6)比例检验
当两样本组中n相同时,pwr.2p.test(h=,n=,sig.level=,power) h是效应值,n是各组相同的样本量,h=2*arcsin(p1^1/2)-s*arcsin(p2^1/2),可用ES.h(p1,p2)函数进行计算;
当两样本组中n不同时,使用函数:pwr.2p2n.test(h,n1=,n2=,sig.level=,power=)
问题:
若对某流行药物能缓解60%使用者的症状感到怀疑,而一种更贵的新药叵能缓解65%使用者的症状,就会被投放到市场中,在研究中需要多少受试者才能够检测到两种药物存在这一特定的差异?假设要90%的把握得出新药更有效的结论,并且希望95%的把握不会误得结论。另只对评价新药是否比标准药物更好感兴趣,因此只需单边检验
- pwr.2p.test(h=ES.h(.65,.6),sig.level=.05,power=.9,alternative="greater")

根据结果可知,为满足以上要求,在本研究中需要1605个试用新药,1605个试用已有药物。
(7)卡方检验
卡方检验常用来评价两个类别变量的关系。
问题:
假设想研究人种与工作晋升的关系,预期样本中70%是白种人,10%是美国黑人,20%西班牙裔人。
且认为相比30%的美国黑人和50%的西班牙裔人,60%的白种人更容易晋升,研究假设的晋升概率如下表所示:
| 人种 | 晋升比例 | 未晋升者比例 |
| 白种人 | 0.42 | 0.28 |
| 美国黑人 | 0.03 | 0.07 |
| 西班牙裔 | 0.10 | 0.10 |
计算假设的效应值
- prob<-matrix(c(.42,.28,.03,.07,.10,.10),byrow=TRUE,nrow=3)
- ES.w2(prob)
计算所需样本大小
- pwr.chisq.test(w=.1853,df=2,sig.level=.05,power=.9)
结果表明,在既定的效应值、功效水平和显著性水平下,该研究需要369个受试者才能检验人种与工作晋升的关系。
(8)在新情况下中选择合适的效应值
功效分析中,若对主题有一定的了解,可根据相应的测量经验,来计算效应值。但若是当面对全新的研究情况,没有任何过去的经验可借鉴时,可根据Cohen提出的一个基准。
Cohen效应值基准
| 统计方法 | 效应值测量 | 建议的效应值基准 | ||
| 小 | 中 | 大 | ||
| t检验 | d | 0.20 | 0.50 | 0.80 |
| 方差分析 | f | 0.10 | 0.25 | 0.40 |
| 线性模型 | f2 | 0.02 | 0.15 | 0.35 |
| 比例检验 | h | 0.20 | 0.50 | 0.80 |
| 卡方检验 | w | 0.10 | 0.30 | 0.50 |
- library(pwr)
- es<-seq(.1,.5,.01)
- nes<-length(es)
- samsize<-NULL
- for(i in 1:nes){
- result<-pwr.anova.test(k=5,f=es[i],sig.level=.05,power=.9)
- samsize[i]<-ceiling(result$n)
- }
- plot(samsize,es,type="l",lwd=2,col="red",
- ylab="Effect Size",
- xlab="Sample Size(per cell)",
- main="One Way ANOVA with Power=.90 and Alpha=.05")
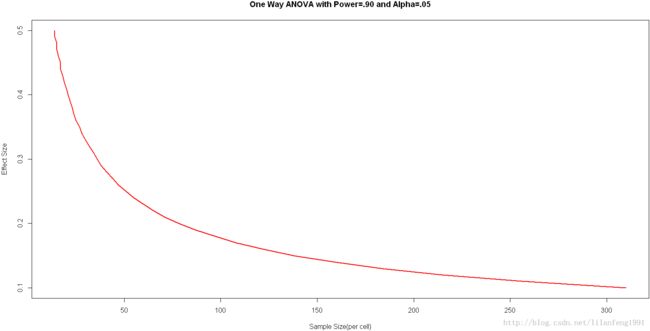
2.绘制功效分析图形
- library(pwr)
- r<-seq(.1,.5,.01)
- nr<-length(r)
- p<-seq(.4,.9,.1)
- np<-length(p)
- samsize<-array(numeric(nr*np),dim=c(nr,np))
- for(i in 1:np){
- for(j in 1:nr){
- result<-pwr.r.test(n=NULL,r=r[j],sig.level=.05,power=p[i],alternative="two.sided")
- samsize[j,i]<-ceiling(result$n)
- }
- }
- xrange<-range(r)
- yrange<-round(range(samsize))
- colors<-rainbow(length(p))
- plot(xrange,yrange,type="n",
- xlab="Correlation Coefficient(r)",
- ylab="Sample Size(n)")
- for(i in 1:np){
- lines(r,samsize[,i],type="l",lwd=2,col=colors[i])
- }
- abline(v=0,h=seq(0,yrange[2],50),lty=2,col=colors[i])
- abline(h=0,v=seq(xrange[1],xrange[2],.02),lty=2,col="gray89")
- title("Sample Size Estimation for Correlation Studies\n Sig=0.05(Two-tailed)")
- legend("topright",title="Power",as.character(p),fill=colors)
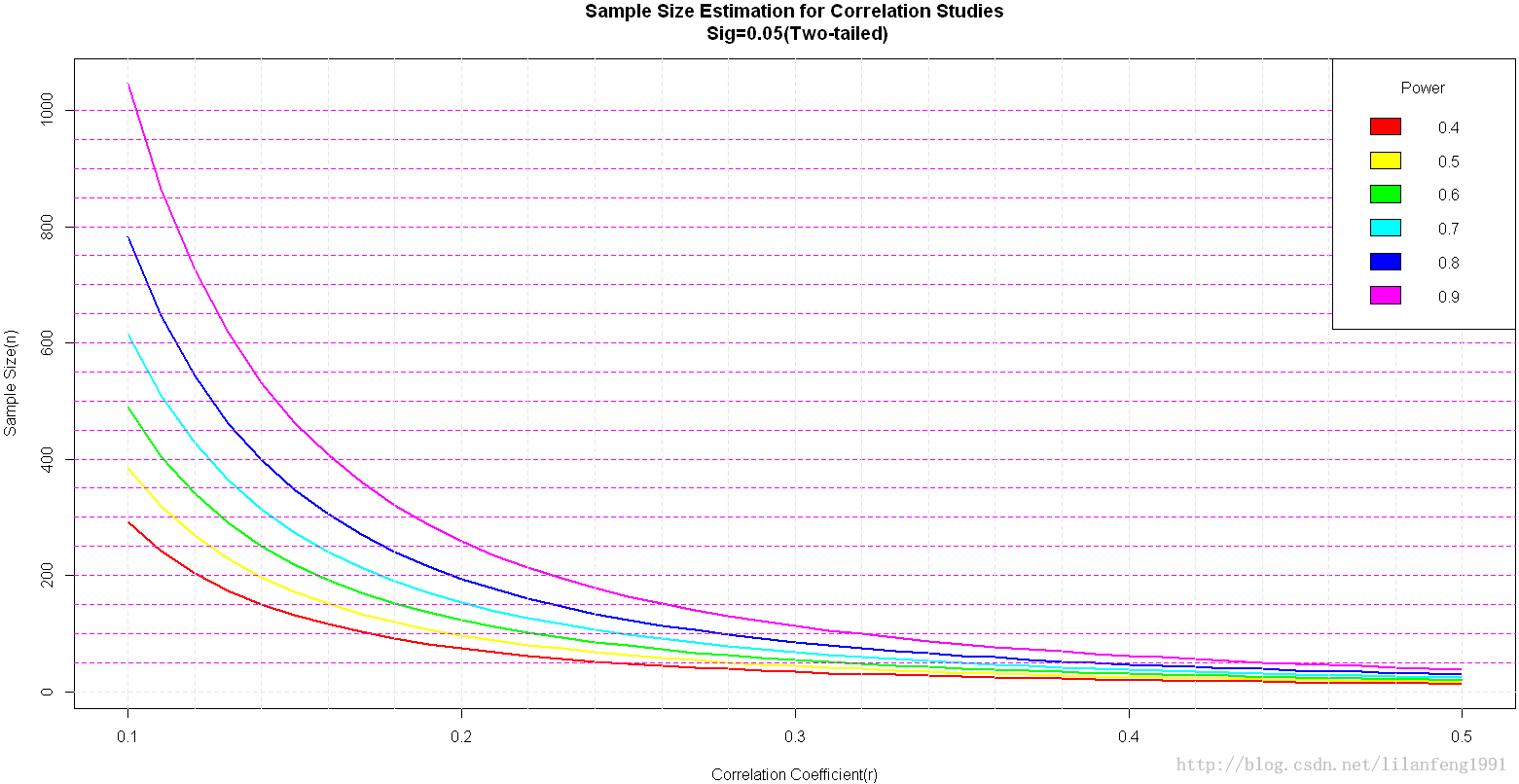
3.其他软件包
- install.packages("piface",repos="http://R-Forge.R-project.org")
- library(piface)
- piface()
| 软件包 | 目的 |
| asypow | 通过渐近似然比方法计算功效 |
| PwrGSD | 组序列设计的功效分析 |
| pamm | 混合模型中随机效应的功效分析 |
| powerSurvEpi | 流行病研究的生存分析中功效和样本量的计算 |
| powerpkg | 患病同胞配对法和TDT(Transmission Disequilibrium Test,传送不均衡检验)设计的功效分析 |
| powerGWASinteraction | GWAS交互作用的功效计算 |
| pedantics | 一些有助于种群基因研究功效分析的函数 |
| gap | 一些病例队列研究设计中计算功效和样本量的函数 |
| ssize.fdr | 微阵列实验中样本量的计算 |