【转载】Beam Search Algorithm (Draft by Andrew Jungwirth)
讲beam search的。从前接触过这个算法,据说这个文章讲得透彻,还没来得急看。原文链接:http://jhave.org/algorithms/graphs/beamsearch/beamsearch.shtml
==================================================================================
Objectives
- To show how the Beam Search Algorithm uses a heuristic function and a given beam width in an attempt to simulate the Breadth-First Search in a memory-efficient way.
- To emphasize the importance of limiting a graph-search's memory consumption when finding solutions to large problem spaces.
- To demonstrate the strengths and weaknesses of the Beam Search Algorithm.
Preparation
In order to understand this algorithm, you must be familiar with the concept of a graph as a group of nodes/vertices and edges connecting these nodes. It is also helpful to understand the how a search tree can be used to show the progress of a graph search. Additionally, knowledge of the Breadth-First Search Algorithm is required because Beam Search is a modification of this algorithm.
Beam Search Algorithm
Even though the Breadth-First Search Algorithm is guaranteed to find the shortest path from a start node to a goal node in an unweighted graph, it is infeasible to use this algorithm on large search spaces because its memory consumption is exponential. This causes the algorithm run out of main memory before a solution can be found to most large, nontrivial problems. For this reason, Beam Search was developed in an attempt to achieve the optimal solution found by the Breadth-First Search Algorithm without consuming too much memory.
In order to accomplish this goal, Beam Search utilizes a heuristic function, h, to estimate the cost to reach the goal from a given node. It also uses a beam width, B, which specifies the number of nodes that are stored at each level of the Breadth-First Search. Thus, while the Breadth-First Search stores all the frontier nodes (the nodes connected to the closing vertices) in memory, the Beam Search Algorithm only stores the B nodes with the best heuristic values at each level of the search. The idea is that the heuristic function will allow the algorithm to select nodes that will lead it to the goal node, and the beam width will cause the algorithm to store only these important nodes in memory and avoid running out of memory before finding the goal state.
Instead of the open list used by the Breadth-First Search Algorithm, the Beam Search Algorithm uses the BEAM to store the nodes that are to be expanded in the next loop of the algorithm. A hash table is used to store nodes that have been visited, similar to the closed list used in the Breadth-First Search. Beam Search initially adds the starting node to the BEAM and the hash table. Then, each time through the main loop of the algorithm, Beam Search adds all of the nodes connected to the nodes in the BEAM to its SET of successor nodes and then adds theB nodes with the best heuristic values from the SET to the BEAM and the hash table. Note that a node that is already in the hash table is not added to the BEAM because a shorter path to that node has already been found. This process continues until the goal node is found, thehash table becomes full (indicating that the memory available has been exhausted), or the BEAM is empty after the main loop has completed (indicating a dead end in the search).
The Beam Search Algorithm is shown by the pseudocode below. This pseudocode assumes that the Beam Search is used on an unweighted graph so the variable g is used to keep track of the depth of the search, which is the cost of reaching a node at that level.
Pseudocode for the Beam Search Algorithm
/* initialization */
g = 0;
hash_table = { start };
BEAM = { start };
/* main loop */
while(BEAM ≠ ∅){ // loop until the BEAM contains no nodes
SET = ∅; // the empty set
/* generate the SET nodes */
for(each state in BEAM){
for(each successor of state){
if(successor == goal) return g + 1;
SET = SET ∪ { successor }; // add successor to SET
}
}
BEAM = ∅; // the empty set
g = g + 1;
/* fill the BEAM for the next loop */
while((SET ≠ ∅) AND (B > |BEAM|)){ // set is not empty and the number of nodes in BEAM is less than B
state = successor in SET with smallest h value;
SET = SET \ { state }; // remove state from SET
if(state ∉ hash_table){ // state is not in the hash_table
if(hash_table is full) return ∞;
hash_table = hash_table ∪ { state }; // add state to hash_table
BEAM = BEAM ∪ { state }; // add state to BEAM
}
}
}
// goal was not found, and BEAM is empty - Beam Search failed to find the goal
return ∞;
Example Trace of the Beam Search Algorithm
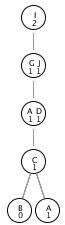
The following traces of the Beam Search Algorithm use two rows to represent each main loop of the algorithm's execution. The first row of each numbered loop displays the nodes added to the SET. These nodes are ordered by their heuristic values, with alphabetical ordering used to sort nodes with identical h values. Since the SET is a mathematical set, if a node is inserted into the SET more than once from multiple parents, it only appears in the SET once. The second row of each numbered loop lists the nodes from the SET that are added to the BEAM in the second part of the main loop. Both rows also display the hash table to show its current state. Notice that the hash table has only seven slots, indicating that the memory size for this example trace is seven. A simple linear hashing scheme with key values determined by the node names' ASCII values mod 7 is used for simplicity. In all three of these lists, nodes are listed in the formatnode_name(predecessor_name). The algorithm is traced four times with different values of B to demonstrate the strengths and weaknesses of the algorithm. Each trace includes a search tree that shows the BEAM at each level of the search. In the graph, the numbers under the node names are the h values for the nodes. These traces show how Beam Search attempts to find the shortest path from node I to node B in the graph shown in Figure 1. (Figure 1 is included above each trace for convenience.)
Trace 1, B = 1
| loop number |
SET (first row per numbered loop) BEAM (second row per numbered loop) |
hash_table |
| BEAM = { I(null) } | hash_table = { _, I(null), _, _, _, _, _ } | |
| 1 | SET = { G(I), J(I), E(I), H(I) } | hash_table = { _, I(null), _, _, _, _, _ } |
| 1 | BEAM = { G(I) } | hash_table = { _, I(null), _, _, _, _, G(I) } |
| 2 | SET = { D(G), J(G), I(G) } | hash_table = { _, I(null), _, _, _, _, G(I) } |
| 2 | BEAM = { D(G) } | hash_table = { _, I(null), _, D(G), _, _, G(I) } |
| 3 | SET = { G(D) } | hash_table = { _, I(null), _, D(G), _, _, G(I) } |
| 3 | BEAM = { } | hash_table = { _, I(null), _, D(G), _, _, G(I) } |
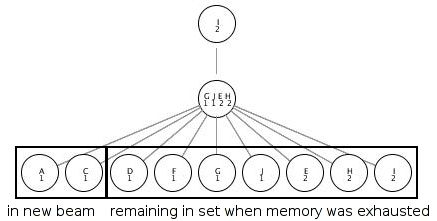
At this point, the BEAM is empty, and the Beam Search Algorithm has reached a dead-end in its search. Since the node G in the SET was already in the hash table, it could not be added to the BEAM, which left the BEAM empty. This trace illustrates the greatest weakness of the Beam Search Algorithm: An inaccurate heuristic function can lead the algorithm into a situation in which it cannot find a goal, even if a path to the goal exists. While increasing the value of B may allow Beam Search to find the goal, increasing B by too much may cause the algorithm to run out of memory before it finds the goal. For this reason, the choice of B has a large impact on Beam Search's performance. Figure 2 shows the BEAM nodes at each level in this dead-end search.
Trace 2, B = 2
| loop number |
SET (first row per numbered loop) BEAM (second row per numbered loop) |
hash_table |
| BEAM = { I(null) } | hash_table = { _, I(null), _, _, _, _, _ } | |
| 1 | SET = { G(I), J(I), E(I), H(I) } | hash_table = { _, I(null), _, _, _, _, _ } |
| 1 | BEAM = { G(I), J(I) } | hash_table = { _, I(null), J(I), _, _, _, G(I) } |
| 2 | SET = { A(J), D(G), G(J), J(G), E(J), I(G) } | hash_table = { _, I(null), J(I), _, _, _, G(I) } |
| 2 | BEAM = { A(J), D(G) } | hash_table = { A(J), I(null), J(I), D(G), _, _, G(I) } |
| 3 | SET = { C(A), G(D), J(A) } | hash_table = { A(J), I(null), J(I), D(G), _, _, G(I) } |
| 3 | BEAM = { C(A) } | hash_table = { A(J), I(null), J(I), D(G), C(A), _, G(I) } |
| 4 | SET = { B(C) [goal found - algorithm returns], A(C) } | hash_table = { A(J), I(null), J(I), D(G), C(A), _, G(I) } |
In this trace, the Beam Search Algorithm successfully found the goal via the path IJACB. Even though a solution was found, this solution is not optimal because IECB is a shorter path to the goal node. Once again, an inaccurate heuristic function reduced the effectiveness of the Beam Search Algorithm. Figure 3 shows the BEAM nodes at each level of the search. Notice that only one node appears in the BEAM at level three in the tree. This demonstrates that Beam Search may not always be able to fill the BEAM at each level in the search. In the last level of the tree, node A was first added to the SET, and then node B (the goal node) was found and caused the search to complete.
Trace 3, B = 3
| loop number |
SET (first row per numbered loop) BEAM (second row per numbered loop) |
hash_table |
| BEAM = { I(null) } | hash_table = { _, I(null), _, _, _, _, _ } | |
| 1 | SET = { G(I), J(I), E(I), H(I) } | hash_table = { _, I(null), _, _, _, _, _ } |
| 1 | BEAM = { G(I), J(I), E(I) } | hash_table = { _, I(null), J(I), _, E(I), _, G(I) } |
| 2 | SET = { A(J), C(E), D(G), F(E), G(J), J(E), E(J), H(E), I(E) } | hash_table = { _, I(null), J(I), _, E(I), _, G(I) } |
| 2 | BEAM = { A(J), C(E), D(G) } | hash_table = { A(J), I(null), J(I), C(E), E(I), D(G), G(I) } |
| 3 | SET = { B(C) [goal found - algorithm returns], A(C), C(A), J(A) } | hash_table = { A(J), I(null), J(I), C(E), E(I), D(G), G(I) } |
With B = 3, the Beam Search Algorithm found the optimal path to the goal. However, the larger beam width caused the algorithm to fill the entire memory available for the hash table. Figure 4 shows the BEAM nodes at each level in the search. In the last level of the tree, nodesA, C, and J were added to the SET, and then the goal node B was found, which caused to search to complete.
Trace 4, B = 4
| loop number |
SET (first row per numbered loop) BEAM (second row per numbered loop) |
hash_table |
| BEAM = { I(null) } | hash_table = { _, I(null), _, _, _, _, _ } | |
| 1 | SET = { G(I), J(I), E(I), H(I) } | hash_table = { _, I(null), _, _, _, _, _ } |
| 1 | BEAM = { G(I), J(I), E(I), H(I) } | hash_table = { H(I), I(null), J(I), _, E(I), _, G(I) } |
| 2 | SET = { A(J), C(E), D(G), F(E), G(J), J(E), E(H), H(E), I(E) } | hash_table = { H(I), I(null), J(I), _, E(I), _, G(I) } |
| 2 | BEAM = { A(J), C(E), D(G) [not enough memory - algorithm returns] } | hash_table = { H(I), I(null), J(I), A(J), E(I), C(E), G(I) } |
Using B = 4, the Beam Search Algorithm quickly ran out of memory. This shows the second major weakness of the Beam Search Algorithm: When Bbecomes large, the algorithm consumes memory very quickly like the Breadth-First Search Algorithm. Figure 5 shows the BEAM at each level in the search. The last level in the tree shows the progress of the search when the algorithm ran out of memory.
Efficiency/Algorithm Analysis
It is generally effective to analyze graph-search algorithms by considering four traits:
- Completeness: A search algorithm is complete if it will find a solution (goal node) when a solution exists.
- Optimality: A search algorithm is optimal if it finds the optimal solution. In the case of the Beam Search Algorithm, this means that the algorithm must find the shortest path from the start node to the goal node.
- Time complexity: This is an order-of-magnitude estimate of the speed of the algorithm. The time complexity is determined by analyzing the number of nodes that are generated during the algorithm's execution.
- Space complexity: This is an order-of-magnitude estimate of the memory consumption of the algorithm. The space complexity is determined by the maximum number of nodes that must be stored at any one time during the algorithm's execution.
Completeness
In general, the Beam Search Algorithm is not complete. This is illustrated in Trace 1 above. Even though the memory was not depleted, the algorithm failed to find the goal because it could not add any nodes to the BEAM. Thus, even given unlimited time and memory, it is possible for the Beam Search Algorithm to miss the goal node when there is a path from the start node to the goal node. A more accurate heuristic function and a larger beam width can improve Beam Search's chances of finding the goal. However, this lack of completeness is one of the foremost weaknesses of the Beam Search Algorithm.
Optimality
Just as the Beam Search Algorithm is not complete, it is also not guaranteed to be optimal. This is shown by Trace 2 above. In this example, Beam Search found the goal node but failed to find the optimal path to the goal, even though the heuristic in Figure 1 is admissible (underestimates the cost to the goal from every node) and consistent (underestimates the cost between neighboring nodes). This happened because the beam width and an inaccurate heuristic function caused the algorithm to miss expanding the shortest path. A more precise heuristic function and a larger beam width can make Beam Search more likely to find the optimal path to the goal.
Time Complexity
The time for the Beam Search Algorithm to complete tends to depend on the accuracy of the heuristic function. An inaccurate heuristic function usually forces the algorithm to expand more nodes to find the goal and may even cause it to fail to find the goal. In the worst case, the heuristic function leads Beam Search all the way to the deepest level in the search tree. Thus, the worst case time is O(Bm), where B is the beam width, and m is the maximum depth of any path in the search tree. This time complexity is linear because the Beam Search Algorithm only expands B nodes at each level; it does not branch out more widely at each level like many search algorithms that have exponential time complexities. The speed with which this algorithm executes is one of its greatest strengths.
Space Complexity
Beam Search's memory consumption is its most desirable trait. Because the algorithm only stores B nodes at each level in the search tree, the worst-case space complexity is O(Bm), where B is the beam width, and m is the maximum depth of any path in the search tree. This linear memory consumption allows Beam Search to probe very deeply into large search spaces and potentially find solutions that other algorithms cannot reach.
Compare with Your Textbook
Algorithms can look differently but still operate in almost the same ways. Compare the pseudocode above with the description in your textbook (if available). Then consider these questions:
- Does your textbook use a hash table to store the nodes that have been expanded? If not, how does it store these nodes?
- Does your textbook explain what type of structure should be used to implement the SET? If so, what structure does it use?
Exploring the Algorithm's Dynamic Behavior
Explore the Algorithm within JHAVÉ
You can practice the Beam Search Algorithm using the algorithm visualization system JHAVÉ. If you have not used JHAVÉ before, please take the time to view the instructions on using JHAVÉ first. If your browser supports Java Webstart, you can launch a visualization of the Beam Search Algorithm directly from this link.
The Beam Search visualization has fifteen example graphs with which you can experiment. The first four examples, perfect1, perfect2,perfect3, and perfect4, have perfect heuristic functions that allow the algorithm to find the optimal path if it has enough memory. The next seven graphs, errant1, errant2, errant3, errant4, errant5, errant6, and errant7, have inaccurate heuristic functions that can lead the algorithm to find paths that are longer than optimal if the beam width is too small. The last four graphs, end1, end2, end3, and end4, result in dead-end searches when using smaller beam widths. For each of these examples, you can set the values for the beam width, B, and the memory size, M, to see how different values of these parameters affect the outcome of the algorithm on the graph. Finally, the level of detail option allows you to control how the animation steps through the pseudocode. The high detail option shows how each node is added to the SET one-by-one and is useful when you are less familiar with the algorithm. The low detail option generates all the nodes in the SET in one step so that you can more easily focus on the other aspects of the algorithm.
Step through the examples in the visualization and test how the different parameters modify the results found by the Beam Search Algorithm. Answer the questions that appear during the visualization to assess your understanding of the algorithm. When you can consistently answer the questions correctly, try the exercises below.
Exercises
- Using the values of B = 2 and M = 10, trace the Beam Search Algorithm on the graph in Figure 6 from start node J to goal node D.
Figure 6
- Did your trace from above find the optimal path from node J to node D? If not, is there a value of B that will find the shortest path with M = 10?
- Is it possible for Beam Search to make a dead-end search (BEAM is empty at the beginning of the main loop) in the graph above (Figure 6) from node J to node D? If so, what value(s) of B produce(s) this situation?
- Modify the heuristic values in the graph above (Figure 6) so that the Beam Search Algorithm can find the optimal path from J to D withB = 1. How much memory is required to find the shortest path in this new graph with B = 1?
Designing Data Sets
Creating input for an algorithm is an effective way to demonstrate your understanding of the algorithm's behavior.
- Design a graph such that Beam Search fails to find the optimal path from the start node to the goal node with
B = 1 but finds this shortest path with B = 2. - Construct a graph so that a Beam Search with B = 2 reaches a dead-end and fails to find the goal node. (Note: Here a dead-end search refers to the situation in which the BEAM is empty at the beginning of the main loop and does not mean the search runs out of memory.)
Modifying the Algorithm
Consider modifying the Beam Search Algorithm as described above so that the lines previously written as
if(hash_table is full) return ∞;
hash_table = hash_table ∪ { state };
BEAM = BEAM ∪ { state };
are reordered as
hash_table = hash_table ∪ { state };
BEAM = BEAM ∪ { state };
if(hash_table is full) return ∞;
Does this have any effect on the results found by the algorithm? Can you devise an example in which the first version of the algorithm finds the goal, but the modified version returns before finding the goal?
Create Your Own Visualization
Using your own source code, presentation software, or manually produced drawings, create your own visualization of the Beam Search Algorithm.
Presentation
Develop a ten-minute presentation on the Beam Search Algorithm that uses the visualization you developed above to explain the strengths and weaknesses of the Beam Search Algorithm.