坐标参数详解
坐标转换的相关问题(椭球体、投影、坐标系统、转换、BEIJING54、XIAN80等...
最近需要将一些数据进行转换,用到了一点坐标转换的知识,发现还来这么复杂^_^,觉得自己真是愧对了武汉大学以及中科院这么多年培养我,让我上了好多课却从来没有好好听,今天才知道其实很有用!不多废话,给您分享下我的坐标转换之路。
Part one: Background
地理坐标系与投影坐标系的区别 (cite from:http://tieba.baidu.com/f?kz=354009166)
1、首先理解地理坐标系(Geographic coordinate system),Geographic coordinate system直译为地理坐标系统,是以经纬度为地图的存储单位的。很明显,Geographic coordinate system是球面坐标系统。我们要将地球上的数字化信息存放到球面坐标系统上,如何进行操作呢?地球是一个不规则的椭球,如何将数据信息以科学的方法存放到椭球上?这必然要求我们找到这样的一个椭球体。这样的椭球体具有特点:可以量化计算的。具有长半轴,短
半轴,偏心率。以下几行便是Krasovsky_1940椭球及其相应参数。
Spheroid: Krasovsky_1940
Semimajor Axis: 6378245.000000000000000000
Semiminor Axis: 6356863.018773047300000000
Inverse Flattening(扁率): 298.300000000000010000
然而有了这个椭球体以后还不够,还需要一个大地基准面将这个椭球定位。在坐标系统描述中,可以看到有这么一行:
Datum: D_Beijing_1954
表示,大地基准面是D_Beijing_1954。
有了Spheroid和Datum两个基本条件,地理坐标系统便可以使用。
完整参数:
Alias:
Abbreviation:
Remarks:
Angular Unit: Degree (0.017453292519943299)
Prime Meridian(起始经度): Greenwich (0.000000000000000000)
Datum(大地基准面): D_Beijing_1954
Spheroid(参考椭球体): Krasovsky_1940
Semimajor Axis: 6378245.000000000000000000
Semiminor Axis: 6356863.018773047300000000
Inverse Flattening: 298.300000000000010000
2、接下来便是Projection coordinate system(投影坐标系统),首先看看投影坐标系统中的一些参数。
Projection: Gauss_Kruger
Parameters:
False_Easting: 500000.000000
False_Northing: 0.000000
Central_Meridian: 117.000000
Scale_Factor: 1.000000
Latitude_Of_Origin: 0.000000
Linear Unit: Meter (1.000000)
Geographic Coordinate System:
Name: GCS_Beijing_1954
Alias:
Abbreviation:
Remarks:
Angular Unit: Degree (0.017453292519943299)
Prime Meridian: Greenwich (0.000000000000000000)
Datum: D_Beijing_1954
Spheroid: Krasovsky_1940
Semimajor Axis: 6378245.000000000000000000
Semiminor Axis: 6356863.018773047300000000
Inverse Flattening: 298.300000000000010000
从参数中可以看出,每一个投影坐标系统都必定会有Geographic Coordinate System。
投影坐标系统,实质上便是平面坐标系统,其地图单位通常为米。
那么为什么投影坐标系统中要存在坐标系统的参数呢?
这时候,又要说明一下投影的意义:将球面坐标转化为平面坐标的过程便称为投影。
好了,投影的条件就出来了:
a、球面坐标
b、转化过程(也就是算法)
也就是说,要得到投影坐标就必须得有一个“拿来”投影的球面坐标,然后才能使用算法去投影!
即每一个投影坐标系统都必须要求有Geographic Coordinate System参数。
3、我们现在看到的很多教材上的对坐标系统的称呼很多,都可以归结为上述两种投影。其中包括我们常见的“非地球投影坐标系统”。):
大地坐标(Geodetic Coordinate):大地测量中以参考椭球面为基准面的坐标。地面点P的位置用大地经度L、大地纬度B和大地高H表示。当点在参考椭球面上时,仅用大地经度和大地纬度表示。大地经度是通过该点的大地子午面与起始大地子午面之间的夹角,大地纬度是通过该点的法线与赤道面的夹角,大地高是地面点沿法线到参考椭球面的距离。
方里网:是由平行于投影坐标轴的两组平行线所构成的方格网。因为是每隔整公里绘出坐标纵线和坐标横线,所以称之为方里网,由于方 里线同时 又是平行于直角坐标轴的坐标网线,故又称直角坐标网。
在1:1万——1:20万比例尺的地形图上,经纬线只以图廓线的形式直接表现出来,并在图角处注出相应度数。为了在用图时加密成 网,在内外图廓间还绘有加密经纬网的加密分划短线(图式中称“分度带”),必要时对应短线相连就可以构成加密的经纬线网。1:2 5万地形图上,除内图廓上绘有经纬网的加密分划外,图内还有加密用的十字线。
我国的1:50万——1:100万地形图,在图面上直接绘出经纬线网,内图廓上也有供加密经纬线网的加密分划短线。
直角坐标网的坐标系以中央经线投影后的直线为X轴,以赤道投影后的直线为Y轴,它们的交点为坐标原点。这样,坐标系中就出现了四 个象限。纵坐标从赤道算起向北为正、向南为负;横坐标从中央经线算起,向东为正、向西为负。
虽然我们可以认为方里网是直角坐标,大地坐标就是球面坐标。但是我们在一副地形图上经常见到方里网和经纬度网,我们很习惯的称经 纬度网为大地坐标,这个时候的大地坐标不是球面坐标,她与方里网的投影是一样的(一般为高斯),也是平面坐标
四、GIS中的坐标系定义与转换
1. 椭球体、基准面及地图投影
GIS中的坐标系定义是GIS系统的基础,正确定义GIS系统的坐标系非常重要。GIS中的坐标系定义由基准面和地图投影两组参数确定,而基准面的定义则由特定椭球体及其对应的转换参数确定,因此欲正确定义GIS系统坐标系,首先必须弄清地球椭球体(Ellipsoid)、大地基准面(Datum)及地图投影(Projection)三者的基本概念及它们之间的关系。 基准面是利用特定椭球体对特定地区地球表面的逼近,因此每个国家或地区均有各自的基准面,我们通常称谓的北京54坐标系、西安80坐标系实际上指的是我国的两个大地基准面。我国参照前苏联从1953年起采用克拉索夫斯基(Krassovsky)椭球体建立了我国的北京54坐标系,1978年采用国际大地测量协会推荐的1975地球椭球体建立了我国新的大地坐标系--西安80坐标系,目前大地测量基本上仍以北京54坐标系作为参照,北京54与西安80坐标之间的转换可查阅国家测绘局公布的对照表。 WGS1984基准面采用WGS84椭球体,它是一地心坐标系,即以地心作为椭球体中心,目前GPS测量数据多以WGS1984为基准。
上述3个椭球体参数如下:
椭球体与基准面之间的关系是一对多的关系,也就是基准面是在椭球体基础上建立的,但椭球体不能代表基准面,同样的椭球体能定义不同的基准面,如前苏联的Pulkovo 1942、非洲索马里的Afgooye基准面都采用了Krassovsky椭球体,但它们的基准面显然是不同的。
地图投影是将地图从球面转换到平面的数学变换,如果有人说:该点北京54坐标值为X=4231898,Y=21655933,实际上指的是北京54基准面下的投影坐标,也就是北京54基准面下的经纬度坐标在直角平面坐标上的投影结果。
2. GIS中基准面的定义与转换
虽然现有GIS平台中都预定义有上百个基准面供用户选用,但均没有我们国家的基准面定义。假如精度要求不高,可利用前苏联的Pulkovo 1942基准面(Mapinfo中代号为1001)代替北京54坐标系;假如精度要求较高,如土地利用、海域使用、城市基建等GIS系统,则需要自定义基准面。
GIS系统中的基准面通过当地基准面向WGS1984的转换7参数来定义,转换通过相似变换方法实现,具体算法可参考科学出版社1999年出版的《城市地理信息系统标准化指南》第76至86页。假设Xg、Yg、Zg表示WGS84地心坐标系的三坐标轴,Xt、Yt、Zt表示当地坐标系的三坐标轴,那么自定义基准面的7参数分别为:三个平移参数ΔX、ΔY、ΔZ表示两坐标原点的平移值;三个旋转参数εx、εy、εz表示当地坐标系旋转至与地心坐标系平行时,分别绕Xt、Yt、Zt的旋转角;最后是比例校正因子,用于调整椭球大小。
MapX中基准面定义方法如下:
Datum.Set(Ellipsoid, ShiftX, ShiftY, ShiftZ, RotateX, RotateY, RotateZ, ScaleAdjust, PrimeMeridian)
其中参数: Ellipsoid为基准面采用的椭球体;
ShiftX, ShiftY, ShiftZ为平移参数;
RotateX, RotateY, RotateZ为旋转参数;
ScaleAdjust为比例校正因子,以百万分之一计;
PrimeMeridian为本初子午线经度,在我国取0,表示经度从格林威治起算。
3. GIS中地图投影的定义
我国的基本比例尺地形图(1:5千,1:1万,1:2.5万,1:5万,1:10万,1:25万,1:50万,1:100万)中,大于等于50万的均采用高斯-克吕格投影(Gauss-Kruger),又叫横轴墨卡托投影(Transverse Mercator);小于50万的地形图采用正轴等角割园锥投影,又叫兰勃特投影(Lambert Conformal Conic);海上小于50万的地形图多用正轴等角园柱投影,又叫墨卡托投影(Mercator),我国的GIS系统中应该采用与我国基本比例尺地形图系列一致的地图投影系统。
在MapX中坐标系定义由基准面、投影两部分参数组成,方法如下:
CoordSys.Set(Type, [Datum], [Units], [OriginLongitude], [OriginLatitude],
[StandardParallelOne], [StandardParallelTwo], [Azimuth], [ScaleFactor],
[FalseEasting], [FalseNorthing], [Range], [Bounds], [AffineTransform])
其中参数:Type表示投影类型,Type为1时地图坐标以经纬度表示,它是必选参数,它后面的参数都为可选参数;
Datum为大地基准面对象,如果采用非地球坐标(NonEarth)无需定义该参数;
Units为坐标单位,如Units为7表示以米为单位;
OriginLongitude、OriginLatitude分别为原点经度和纬度;
StandardParallelOne、StandardParallelTwo为第一、第二标准纬线;
Azimuth为方位角,斜轴投影需要定义该参数;
ScaleFactor为比例系数;
FalseEasting, FalseNorthing为东伪偏移、北伪偏移值;
Range为地图可见纬度范围;
Bounds为地图坐标范围,是一矩形对象,非地球坐标(NonEarth)必须定义该参数;
AffineTransform为坐标系变换对象。
相应高斯-克吕格投影、兰勃特投影、墨卡托投影需要定义的坐标系参数序列如下:
高斯-克吕格:投影代号(Type),基准面(Datum),单位(Unit),
中央经度(OriginLongitude),原点纬度(OriginLatitude),
比例系数(ScaleFactor),
东伪偏移(FalseEasting),北纬偏移(FalseNorthing)
兰勃特: 投影代号(Type),基准面(Datum),单位(Unit),
中央经度(OriginLongitude),原点纬度(OriginLatitude),
标准纬度1(StandardParallelOne),标准纬度2(StandardParallelTwo),
东伪偏移(FalseEasting),北纬偏移(FalseNorthing)
墨卡托: 投影代号(Type),基准面(Datum),单位(Unit),
原点经度(OriginLongitude),原点纬度(OriginLatitude),
标准纬度(StandardParallelOne)
在城市GIS系统中均采用6度或3度分带的高斯-克吕格投影,因为一般城建坐标采用的是6度或3度分带的高斯-克吕格投影坐标。高斯-克吕格投影以6度或3度分带,每一个分带构成一个独立的平面直角坐标网,投影带中央经线投影后的直线为X轴(纵轴,纬度方向),赤道投影后为Y轴(横轴,经度方向),为了防止经度方向的坐标出现负值,规定每带的中央经线西移500公里,即东伪偏移值为500公里,由于高斯-克吕格投影每一个投影带的坐标都是对本带坐标原点的相对值,所以各带的坐标完全相同,因此规定在横轴坐标前加上带号,如(4231898,21655933)其中21即为带号,同样所定义的东伪偏移值也需要加上带号,如21带的东伪偏移值为21500000米。
假如你的工作区位于21带,即经度在120度至126度范围,该带的中央经度为123度,采用Pulkovo 1942基准面,那么定义6度分带的高斯-克吕格投影坐标系参数为:(8,1001,7,123,0,1,21500000,0)。
那么当精度要求较高,实测数据为WGS1984坐标数据时,欲转换到北京54基准面的高斯-克吕格投影坐标,如何定义坐标系参数呢?你可选择WGS 1984(Mapinfo中代号104)作为基准面,当只有一个已知控制点时(见第2部分),根据平移参数调整东伪偏移、北纬偏移值实现WGS84到北京54的转换,如: (8,104,7,123,0,1,21500200,-200),也可利用 AffineTransform坐标系变换对象,此时的转换系数(A、B、C、D、E、F)中A、B、D、E为0,只有X、Y方向的平移值C、F ;当有3个已知控制点时,可利用得到的转换系数(A、B、C、D、E、F)定义 AffineTransform坐标系变换对象,实现坐标系的转换,如:(8,104,7,123,0,1,21500000,0,map.AffineTransform),其中AffineTransform定义为AffineTransform.set(7,A、B、C、D、E、F)(7表示单位米);当然有足够多已知控制点时,直接求定7参数自定义基准面就行了。
.userData { BEHAVIOR. url(#default#userdata) }
Part Two: About BEIJING54
美国国家测绘局(National Imagery and Mapping Agency)公布了世界大多数国家的当地基准面至WGS1984基准面的转换3参数(平移参数),可从 http://164.214.2.59/GandG/wgs84dt/dtp.html 下载,其中包括有香港Hong Kong 1963基准面、台湾 Hu-Tzu-Shan 基准面的转换3参数,但是没有中国大陆的参数。
实际工作中一般都根据工作区内已知的北京54坐标控制点计算转换参数,如果工作区内有足够多的已知北京54与WGS84坐标控制点,可直接计算坐标转换的7参数或3参数;当工作区内有3个已知北京54与WGS84坐标控制点时,可用下式计算WGS84到北京54坐标的转换参数(A、B、C、D、E、F):x54 = AX84 + BY84 + C,y54 = DX84 + EY84 + F,多余一点用作检验;在只有一个已知控制点的情况下(往往如此),用已知点的北京54与WGS84坐标之差作为平移参数,当工作区范围不大时精度也足够了。
从Mapinfo中国的URL(http://www.mapinfo.com.cn/download)可下载到包含北京54、西安80坐标系定义的Mapinfow.prj文件,其中定义的北京54基准面参数为:(3,24,-123,-94,-0.02,0.25,0.13,1.1,0),西安80基准面参数为:(31,24,-123,-94,-0.02,0.25,0.13,1.1,0),文件中没有注明其参数的来源,我发现它们与Mapinfo参考手册附录G"定义自定义基准面"中的一个例子所列参数相同,因此其可靠性值得怀疑,尤其从西安80与北京54采用相同的7参数来看,至少西安80的基准面定义肯定是不对的。因此,当系统精度要求较高时,一定要对所采用的参数进行检测、验证,确保坐标系定义的正确性。
(cite from:http://bbs.esrichina-bj.cn/ESRI/viewthread.php?tid=33238&highlight=beijing54)
<<使用project工具wgs84到beijing54的投影转换应该需要转换七参数吧~
但是使用arcmap中的导出功能时,可以把数据按照data frame的投影方式导出,如果把一幅84的地图按照54的数据框架导出,这个时候导出的数据是否实现了从84到54的转变?若实现了,可是没有输入转换七参数啊~若没有实现,也只是定义了坐标系统而已吗?
>>gis27:这个问题我也思考过,后来觉得ArcMap中的动态投影时针对我国的Beijing54或Xi'an80和其他坐标系统转换时,由于Datum不同,需要转换参数,而我国的转换参数不公开,那么ArcMap如何做到的呢,有2中猜测,
第一、ESRI会将不知道转换参数的情况下将转换参数全设置为0
第二、ESRI有自己的参照方法
我更倾向于第一种,但自己没有实际测试过
以下是ESRI官方的回答(cite from:http://support.esri.com/index.cfm?fa=knowledgebase.techarticles.articleShow&d=32082)
Question
Answer
No, the datum transformation parameters for the Beijing 1954 datum are not available. The People's Republic of China does not publish these parameters as they are deemed a National security issue.
HowTo: Apply custom geographic (datum) transformation and project data in ArcMap.
| Article ID: | 23217 |
|---|---|
| Software: | ArcGIS - ArcEditor 8.1.2, 8.2, 8.3, 9.0, 9.1 ArcGIS - ArcInfo 8.1.2, 8.2, 8.3, 9.0, 9.1 ArcGIS - ArcView 8.1.2, 8.2, 8.3, 9.0, 9.1 |
| Platforms: | N/A |
Summary
Procedure
- Open ArcMap with a new, empty map, and add the dataset which has the projection defined, that you want to project to a new coordinate system.
- Click View > Data Frame Properties > Coordinate System tab.
- In the 'Select a Coordinate System:' box, open Predefined, and from the available coordinate systems, select the output projection and datum required, then click Apply.
- Click on the Transformations button, and in the Geographic Coordinate System Transformations GUI, verify that the "Convert from" and "into" boxes are correctly populated.
- Click New, and from the Method Name dropdown list, select the correct transformation method from the available choices.
- Enter the required parameters, then click OK on the New Geographic Transformations dialog.
- Click OK on the Geographic Coordinate System Transformations dialog.
- Click OK on the Data Frame Properties dialog.
- Right-click on the layer name in the ArcMap Table of Contents (TOC); click Data > Export
data > All Features, and select 'Use the same coordinate system as the data frame'. - Set the output location, name the new dataset, and click OK. The new shapefile or geodatabase feature class will be written in the desired location, in the new coordinate system.
To help with similar issues in the future, you can download the EPSG
database of projections, datum transformation parameters, and get other useful information at the EPSG Web site.
The EPSG (European Petroleum Survey Group) database contains parameters for over 1,800 coordinate systems, and over 800 datum transformations, as well as a wealth of other projection-related information.
我将MAPINFO 的七参数(24,-123,-94,-0.02,0.25,0.13,1.1,0)输入到ARCGIS中,其步骤如下:
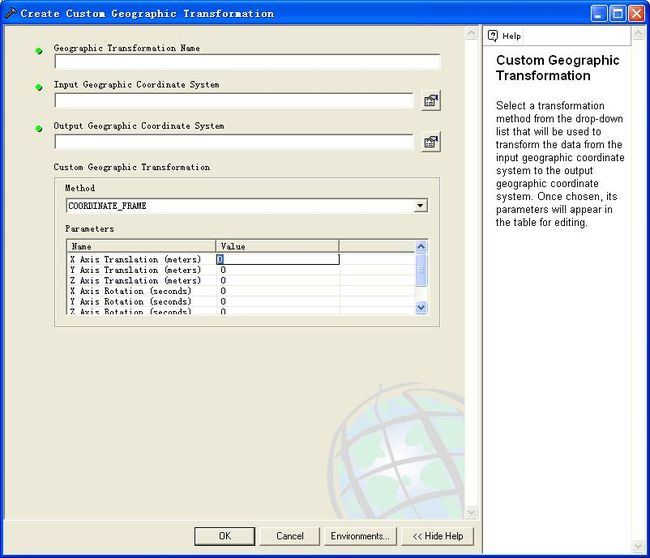
Data Management Tools --> Projection and Transformatioin --> Create custom Geographic Transformation 如下图所示:
选择 coordinate_frame并输入新的七个参数 ,得到一个新的从WGS_84到 BEIJING54的转换函数,
然后使用Data Management Tools --> Projection and Transformatioin --> 中的RASTER 或者FEATURE方法转换 或者按《Coordinate Transformation of Hong Kong Spatial Data in ArcGIS Desktop》白皮书中方法,但结果并不好,结果变形很明显:
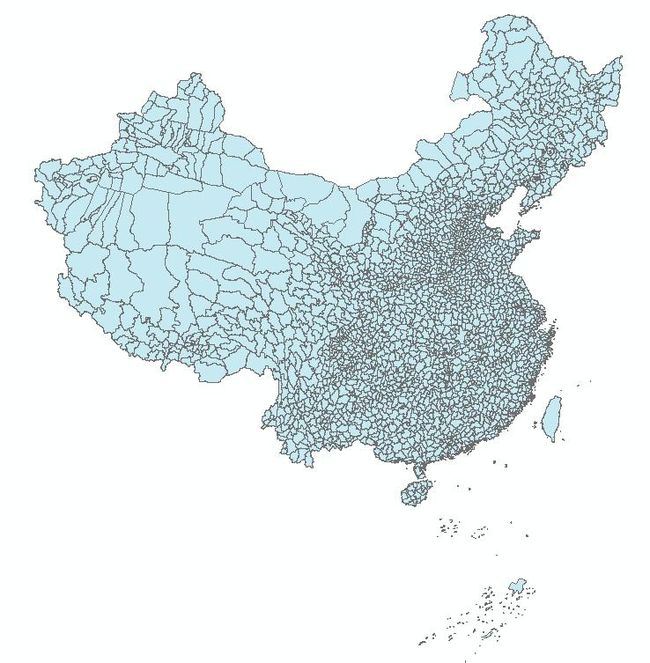
(1)BEIJING54 BEFORE TRANSFORM
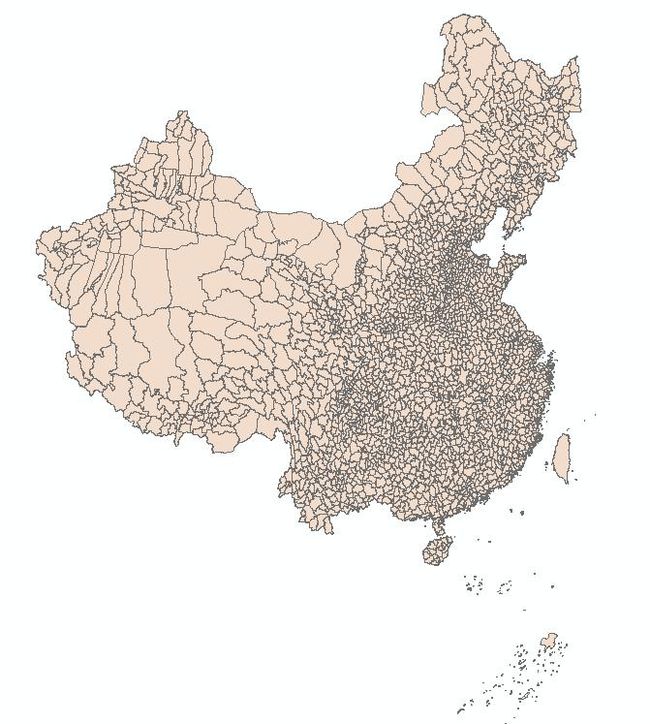
(2)WGS_84 AFTER TRANSFORM
(3) 如果不转换直接保留WGS——84坐标系,或者从其它坐标系(如L/L经纬度),如下图,变形并不大:
PART THREE: OTHERS
一、北京54坐标到西安80坐标转换小结
1、北京54和西安80是两种不同的大地基准面,不同的参考椭球体,因而两种地图下,同一个点的坐标是不同的,无论是三度带六度带坐标还是经纬度坐标都是不同的。
2、数字化后的得到的坐标其实不是WGS84的经纬度坐标,因为54和80的转换参数至今没有公布,一般的软件中都没有54或80投影系的选项,往往会选择WGS84投影。
3、WGS84、北京54、西安80之间,没有现成的公式来完成转换。
4、对于54或80坐标,从经纬度到平面坐标(三度带或六度带)的相互转换可以借助软件完成。
5、54和80间的转换,必须借助现有的点和两种坐标,推算出变换参数,再对待转换坐标进行转换。(均靠软件实现)
6、在选择参考点时,注意不能选取河流、等高线、地名、高程点,公路尽量不选。这些在两幅地图上变化很大,不能用作参考。而应该选择固定物,如电站,桥梁等。
二、西安80坐标系与北京54坐标系转换
西安80坐标系与北京54坐标系其实是一种椭球参数的转换作为这种转换在同一个椭球里的转换都是严密的,而在不同的椭球之间的转换是不严密,因此不存在一套转换参数可以全国通用的,在每个地方会不一样,因为它们是两个不同的椭球基准。那么,两个椭球间的坐标转换,一般而言比较严密的是用七参数布尔莎模型,即 X 平移, Y 平移, Z 平移, X 旋转(WX), Y 旋转(WY), Z 旋转(WZ),尺度变化(DM )。要求得七参数就需要在一个地区需要 3 个以上的已知点。如果区域范围不大, 最远点间的距离不大于 30Km( 经验值 ) ,这可以用三参数,即 X 平移, Y 平移, Z 平移,而将 X 旋转, Y 旋转, Z 旋转,尺度变化面DM视为 0 。
在MAPGIS平台中实现步骤:
第一步:向地方测绘局(或其它地方)找本区域三个公共点坐标对(即54坐标x,y,z和80坐标x,y,z);
第二步:将三个点的坐标对全部转换以弧度为单位。(菜单:投影转换/输入单点投影转换,计算出这三个点的弧度值并记录下来)
第三步:求公共点求操作系数(菜单:投影转换/坐标系转换)。如果求出转换系数后,记录下来。
第四步:编辑坐标转换系数。(菜单:投影转换/编辑坐标转换系数。)最后进行投影变换,“当前投影”输入80坐标系参数,“目的投影”输入54坐标系参数。进行转换时系统会自动调用曾编辑过的坐标转换系数。
如何实现从wgs-84到beijing54的坐标转换(cite from: 瑞诺新图)
摘要:关于这个坐标系的转化网上有很多文章探讨了各种转换的方法。通过自己的学习,我自己做了一下总结,同时给出了其中要遇到的部分术语和数据,方便以后查阅使用。
主要介绍的是:3参数(七参数)转换法,三参数坐标纠正法
一:3参数(七参数)转换法
从本质上来说,转换的步骤应该大致遵循这样的规则:
首先,将84的经纬度坐标(B84,L84,H84)转换为以地心为中心点的大地坐标(X84,Y84,Z84);
然后根据七参数法(或3参数法)将其转换为54下的地心坐标(X54,Y54,Z54);
然后根据54下的椭球参数,将第二步得到的地心坐标转换为大地坐标(B54,L54,H54);
最后根据工程需要以及各种投影(如高斯克吕格)规则进行投影得到对应的投影坐标。
只有在第二步的时候涉及到七个参数的计算,其他的步骤都有现成的公式可供计算,稍后我会将各种论文贴上来。如果这里涉及到您的利益还请跟我联系,我将马上删除下载链接,我本意只是用于学习使用。
其实如果在公司或者做项目的时候,当对这起个参数要求的很急的时候,我们可以从政府部门或者通过坐标转换软件求出这七个参数或者三个参数,这个可以大大提高效率,节省时间。这些坐标转换软件有:坐标转换大师(这个不错),coorconvert.exe(一般),COORD.exe(这个不错)。
一旦求出了七个参数,可以进行坐标转换的软件除了上述这些小软件可以进行转换外,一些比较有名的GIS开发软件或者开发平台都提供了利用七个参数转换整个数据的功能或者提供了转换单个点的功能,这些在ARC GIS,superMap,mapGis中都有。
二:三参数坐标纠正法
这个方法是这次我在实践中得出来的。因为求出七个参数太过麻烦,所以选用了本方法。本方法的使用范围为:大比例尺地形图比较适用,如县范围等。
具体方法:
1.从测区取出适量的坐标控制点,坐标控制点是些这样的点,他们拥有84下的经纬度坐标,同时也拥有54下的投影坐标;
2.取出后利用将经纬度坐标在esupermap平台中编写程序将其转成84下的高斯克吕格投影坐标(可以看成是一种虚假的投影);
3.由2步中得到的投影坐标和原54下的投影坐标相比较得到一个差值p1(x1,y1,z1),并将其保存起来;
4.重复第二步一直到把所有的点都计算完,计算完后将差值进行汇总并得到一个平均值p(x,y,z).
通过此方法得到的三个参数经过测试和验证,他的精度在厘米或者亚米级的进度,这个对于一般的定位来说已经足够了。他正宗的参数法法的精度还要高。
总结:当然,如果要提高精度的话,最好还是用七参数法,他的定位精度基本上都在厘米或者毫米级。
54大地参数:
参考椭球体:Krasovsky_1940
长半轴:6378245
短半轴:6356863.0188
扁率:298.3
84大地参数:
参考椭球体:WGS 84
长半轴:6378137
短半轴:6356752.3142
扁率:298.257224
80大地参数:
参考椭球体:IAG 75
长半轴:6378140
短半轴:6356755.2882
扁率:298.257000
评:个人认为该作者从GPS结合的角度来转换坐标不失为一个很好的方法,但仅对于小区域和大比例尺有效。 对于全国范围,迫切需要的是统一的七参数或者三参数模型,才能得到一个较好的转换结果。
更多的关于 地图投影及坐标转换的系统知识 ,请参见 祝国瑞 先生的 《地图学》,祝老师终其一生的精力致力于此领域,让人钦偑,其著作很详实且用心。当时上课时还能自己推算各个投影带及各种参数的设置,可惜现在什么都不懂了,劝正在学校的大学生们一定要好好自己的专业学习!