Andrew Stankevich's Contest #2 Solution
Andrew Stankevich's Contest #2
Solution
Problem A: NonAbsorbing DFA
Problem B: TheTowers of Hanoi Revisited
Problem C:Hyperhuffman
Problem D: LittleJumper
Problem E:Quantization Problem
Problem F: Roads
Problem G:Robbers
Problem H: ToralTickets
July 30th,2013 by chlxyd,xioumu
Problem A:Non Absorbing DFA
给一个编译原理中的DFA图,图有一个起点,多个终点,图的边表示为一个F矩阵,f[i][j]表示i点用字母j可以连向f[i][j]点。还给了一个G,对于G[i][j] = 1表示,i点用字母j连出去的边时空边(也就是不会消耗字母j).
求有多少不同的长度为N的字符串符合这个DFA图(可以重起点走到终点)
Solution
Tag:图论,DP
若没有空边的话,直接用个简单的Dp就可以求出答案了,所以现在只要处理掉空边就行了。
若G(I,j)空边组成了一个环,那么到I节点的字母j永远不会走出环。所以若存在环,直接把环上的边都删了就行。
若G(i,j)没有组成环,那么直接把的G(I,j)指向这条路径上第一条非空边指向的点即可。
/*
* Author: chlxyd
* Created Time: 2013/7/20 14:36:12
* File Name: A.cpp
*/
#include<iostream>
#include<sstream>
#include<fstream>
#include<vector>
#include<list>
#include<deque>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cmath>
#include<ctime>
using namespace std;
const double eps(1e-8);
typedef long long lint;
#define clr(x) memset( x , 0 , sizeof(x) )
#define sz(v) ((int)(v).size())
#define rep(i, n) for (int i = 0; i < (n); ++i)
#define repf(i, a, b) for (int i = (a); i <= (b); ++i)
#define repd(i, a, b) for (int i = (a); i >= (b); --i)
#define clrs( x , y ) memset( x , y , sizeof(x) )
const int maxn = 1000 + 10;
int vs[maxn], vt[maxn], v[maxn];
int n, m, len, S, tn;
char word[maxn];
vector<int> e[maxn], wo[maxn], g[maxn];
void add(vector<int> *e, vector<int> *wo, int x, int y, int w) {
e[x].push_back(y);
wo[x].push_back(w);
}
void add2(int x, int y) {
g[x].push_back(y);
}
void init() {
scanf("%s", word);
m = strlen(word);
scanf("%d", &n);
scanf("%d%d", &S, &tn);
clr(vs);
clr(vt);
S--;
vs[S] = 1;
rep (i, tn) {
int x;
scanf("%d", &x);
x--;
vt[x] = 1;
}
rep (i, n) {
e[i].clear();
g[i].clear();
wo[i].clear();
}
//printf("%d %d\n", n, m);
rep (i, n)
rep (j, m) {
int x;
scanf("%d", &x);
x--;
add(e, wo, i, x, j);
}
rep (i, n)
rep (j, m) {
int x;
scanf("%d", &x);
add2(i, x);
}
scanf("%d", &len);
//printf("%d\n", len);
}
int dfs(int x, int w) {
if (v[x]) return -1;
v[x] = 1;
rep (i, sz(e[x])) {
if (w == wo[x][i]) {
int j = e[x][i];
if (g[x][i]){
int h = dfs(j, w);
if (h == -1)
return -1;
e[x][i] = h;
g[x][i] = 0;
return h;
}
else if (!g[x][i]) {
return j;
}
}
}
return -1;
}
void getG2() {
rep (i, n) {
rep (k, sz(e[i])) {
if (g[i][k]) {
memset(v, 0, sizeof(v));
dfs(i, wo[i][k]);
}
}
}
}
void add(vector<int> &a, vector<int> b) {
int an = sz(a), bn = sz(b);
rep (i, min(an, bn)) {
a[i] += b[i];
}
repf (i, an, bn - 1) {
a.push_back(b[i]);
}
rep (i, max(an, bn)) {
if (a[i] >= 10) {
if (i + 1 >= sz(a))
a.push_back(0);
a[i + 1] += a[i] / 10;
a[i] %= 10;
}
}
}
void myset(vector<int> &a, int w) {
a.clear();
a.push_back(w);
}
void myput(vector<int> &a) {
repd (i, sz(a) - 1, 0) {
printf("%d", a[i]);
}
puts("");
}
vector<int> f[70][maxn];
//int f[70][maxn];
void gao(int l, int w) {
if (sz(f[l][w]) != 0) return;
//if (f[l][w] != -1) return;
if (l == 0) {
if (vt[w] == 0) {
//f[l][w] = 0;
myset(f[l][w], 0);
}
else {
//f[l][w] = 1;
myset(f[l][w], 1);
}
//printf("%d: %d %d %d\n", vvt[w], l, w, f[l][w]);
return ;
}
//f[l][w] = 0;
myset(f[l][w], 0);
rep (i, sz(e[w])) {
int j = e[w][i];
if (g[w][i] == 0) {
gao(l - 1, j);
//f[l][w] = f[l][w] + f[l - 1][j];
add(f[l][w], f[l - 1][j]);
}
}
//printf("%d %d %d\n", l, w, f[l][w]);
}
void workDP() {
repf (i, 0, len)
repf (j, 0, n)
f[i][j].clear();
//memset(f, -1, sizeof(f));
gao(len, S);
//printf("%d\n", f[len][S]);
myput(f[len][S]);
}
int main(){
int T;
scanf("%d", &T);
rep(ca, T) {
if (ca != 0) puts("");
init();
getG2();
workDP();
}
return 0;
}
Problem B: The Towers of Hanoi Revisited
N个盘,m个柱子的汉诺塔,问把所有盘子移到m柱子的最小步数。
Solution
Tag:DP
Dp[i][j]表示用j个柱子把i个盘子移到最后一个盘子的最小步数,那么我们的策略一定是把k个盘子移到某一个柱子上,然后把剩下i-k个盘子用j-1个柱子移到最后,最后把k个盘子用j个柱子移到最后,dp[i][j]=min(dp[k][j]*2+dp[i-k][j-1]).dp同时记录路径,然后再按照路径做一次dfs把方案输出。
#pragma comment(linker, "/STACK:102400000,102400000")
/*
* Author: chlxyd
* Created Time: 2013/7/20 13:39:39
* File Name: B.cpp
*/
#include<iostream>
#include<sstream>
#include<fstream>
#include<vector>
#include<list>
#include<deque>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cmath>
#include<ctime>
using namespace std;
const double eps(1e-8);
typedef long long lint;
#define clr(x) memset( x , 0 , sizeof(x) )
#define sz(v) ((int)(v).size())
#define rep(i, n) for (int i = 0; i < (n); ++i)
#define repf(i, a, b) for (int i = (a); i <= (b); ++i)
#define repd(i, a, b) for (int i = (a); i >= (b); --i)
#define clrs( x , y ) memset( x , y , sizeof(x) )
stack<int> top[100] ;
vector<string> ret ;
int n , m ;
int topp ;
struct vtype {
int n , dir , s , t , use ;
vtype (int _n = 0, int _dir = 0 , int _s = 0 , int _t = 0 , int _use = 0 ) :
n(_n),dir(_dir),s(_s),t(_t),use(_use){
}
};
long long f[100][100] ;
int g[100][100] ;
void move( int n , int dir , int s , int t , int use ) {
//cout<<n<<" "<<dir<<" "<<s<<" "<<t<<" "<<use<<endl;
if ( n == 1 ) {
if ( top[t].empty() )
printf("move %d from %d to %d\n" , n + dir , s , t ) ;
else if ( !top[t].empty() )
printf("move %d from %d to %d atop %d\n" , n + dir , s , t , top[t].top() ) ;
top[s].pop() ; top[t].push(n+dir) ;
return ;
}
int jl = 1 ;
repf( i , 1 , m ) {
if ( i == t ) continue ;
if ( top[i].size() == 0 || dir + 1 < top[i].top() ) {
move( g[n][use] , dir , s , i , use ) ;
jl = i ;
break ;
}
}
move( n - g[n][use] , dir + g[n][use] , s , t , use - 1 ) ;
move( g[n][use] , dir , jl , t , use ) ;
}
long long dfs( int i ,int j ) {
if ( j == 3 ) {
g[i][j] = i - 1 ;
if ( i >= 63 ) i = 60 ;
return (1LL<<i)-1;
}
if ( i == 1 ) {
return f[i][j] = 1 ;
}
if ( f[i][j] ) return f[i][j] ;
repf( k , 1 , i - 1 ) {
if ( f[i][j] == 0 || f[i][j] > dfs(k,j) * 2 + dfs(i-k,j-1) ) {
g[i][j] = k ;
f[i][j] = dfs(k,j) * 2 + dfs(i-k,j-1) ;
}
}
return f[i][j] ;
}
int main(){
//freopen("B.in","r",stdin);
//freopen("B.out","w",stdout);
int T ;
scanf("%d" , &T ) ;
bool first = true ;
while ( scanf("%d %d" , &n , &m ) == 2 ) {
if ( !first ) puts("") ;
first = false ;
topp = 0 ;
repf( i , 1 , m ) {
while ( !top[i].empty() ) {
top[i].pop() ;
}
}
printf("%lld\n" , dfs(n,m) ) ;
repd( i , n , 1 ) top[1].push(i) ;
move( n , 0 , 1 , m , m ) ;
}
}
Problem C: Hyperhuffman
按照哈弗曼编码对字符编码,问一篇文章的长度。
Solution
Tag:贪心
按照哈弗曼编码的规则,每次从集合中取两个最小的形成一个新节点就可以了。同时记录一下每个点的高度。最后求出各个叶子的高度。
/*
* Author: chlxyd
* Created Time: 2013/7/20 12:54:56
* File Name: C.cpp
*/
#include<iostream>
#include<sstream>
#include<fstream>
#include<vector>
#include<list>
#include<deque>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cmath>
#include<ctime>
using namespace std;
const double eps(1e-8);
typedef long long lint;
#define clr(x) memset( x , 0 , sizeof(x) )
#define sz(v) ((int)(v).size())
#define rep(i, n) for (long long i = 0; i < (n); ++i)
#define repf(i, a, b) for (long long i = (a); i <= (b); ++i)
#define repd(i, a, b) for (long long i = (a); i >= (b); --i)
#define clrs( x , y ) memset( x , y , sizeof(x) )
multiset<pair<long long ,int> > st ;
#define maxn 500010
long long n , T ;
int a[maxn] ;
int h[maxn*2] ;
int now[maxn][3] ;
int main(){
scanf("%lld" , &T ) ;
repf( t , 1 , T ) {
if ( t != 1 ) puts("");
st.clear() ;
scanf("%lld" , &n ) ;
repf( i, 1 , n ) {
scanf("%d" , &a[i] ) ;
st.insert(make_pair(a[i],i)) ;
}
repf( i , 1 , n * 2 ) h[i] = 1 ;
long long top = n ;
repf( i , 1 , n - 1 ) {
pair<long long,int> x = *st.begin() ;
st.erase(x) ;
pair<long long,int> y = *st.begin() ;
st.erase(y) ;
now[i][0] = x.second;
now[i][1] = y.second;
now[i][2] = top + 1 ;
h[top+1] = 1 ;
st.insert(make_pair(x.first+y.first,++top));
}
//repf( i , 1 , 5 ) cout<<h[i]<<endl;
repd( i , n - 1 , 1 ) {
h[now[i][0]] = h[now[i][2]] + 1 ;
h[now[i][1]] = h[now[i][2]] + 1 ;
}
//repf( i , 1 , n ) cout<<h[i]<<endl;
long long ans = 0 ;
repf( i , 1 , n ) ans += (h[i]-1) * a[i] ;
printf("%lld\n" , ans ) ;
}
}
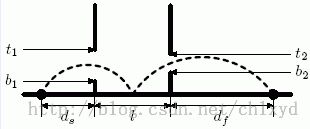
Problem D: Little Jumper
一只青蛙从左边的洞跳到中间,然后跳到右边的洞,问它最小的最大的起跳速度。
Solution
Tag:物理
有一个很直观的感觉就是在中间某个位置的时候最大速度是最小的,然后向两边就递增。
于是三分中间停留点,然后问题被分为相同的两个部分(左边和右边),答案为两者的大值。
对于已经知道起点和终点的情况,可以通过物理(数学?)公式计算得出当前的最小速度。
/*
* Author: chlxyd
* Created Time: 2013/7/21 15:49:49
* File Name: D.CPP
*/
#include<iostream>
#include<sstream>
#include<fstream>
#include<vector>
#include<list>
#include<deque>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cmath>
#include<ctime>
using namespace std;
const double eps(1e-8);
typedef long long lint;
#define clr(x) memset( x , 0 , sizeof(x) )
#define sz(v) ((int)(v).size())
#define rep(i, n) for (int i = 0; i < (n); ++i)
#define repf(i, a, b) for (int i = (a); i <= (b); ++i)
#define repd(i, a, b) for (int i = (a); i >= (b); --i)
#define clrs( x , y ) memset( x , y , sizeof(x) )
int sgn( double x ) {
return ( x > eps ) - ( x < - eps ) ;
}
double b1 , t1 , b2 , t2 , ds , df , g , l ;
double vfind( double x1 , double x2 , double k ) {
return g * (x2-x1) * ( 1 + k * k ) / ( 2 * k ) ;
}
double calc( double x1 , double x2 , double b , double t ) {
//cout<<x1<<" "<<x2<<" "<<b<<" "<<t<<endl;
double da = b / (x1*x2) ;
double ua = t / (x1*x2) ;
da = 2 * da * x1 - da * ( x1 + x2 ) ;
ua = 2 * ua * x1 - ua * ( x1 + x2 ) ;
if ( sgn( da - ua) > 0 ) swap( da , ua ) ;
//cout<<da<<" "<<ua<<endl;
if ( sgn( da - 1)<=0 && sgn( 1 - ua ) <= 0 )
return vfind( x1 , x2 , 1 ) ;
else if ( sgn( 1 - da) < 0 ) return vfind( x1 , x2 , da ) ;
else return vfind( x1 , x2 , ua ) ;
}
double cal( double len ) {
return max( calc( -ds , len , b1 , t1 ) , calc( -df , l - len , b2 , t2 ) ) ;
}
double solve() {
double L = 0 , R = l ;
double mid , midmid ;
repf( i , 1 , 100 ) {
mid = ( L + R ) / 2 ;
midmid = ( mid + R ) / 2 ;
if ( sgn( cal(mid) - cal(midmid) ) > 0 ) L = mid ;
else R = midmid ;
}
return sqrt(cal(( L + R ) / 2)) ;
}
int main(){
while ( scanf("%lf %lf %lf %lf %lf %lf %lf %lf" , &b1 , &t1 , &b2 , &t2 , &l , &ds , &df, &g ) == 8 ) {
//return 0 ;
printf("%.6lf\n" , solve() ) ;
}
}
Problem E: Quantization Problem
有n个组,每组都是m个元素,你原先有一个长为x的序列,你最开始在第一组,然后每一次从这一组中选择一个数,根据你选的下标,下次在下标对应的那个组里面选,一直选到x个,最后要选出来的数字和原先的序列差之和最小。
Solution
Tag:DP
DP[i][j]表示选到了第i个长度,在第j个元组里面选,那么DP[i+1][k] = min( dp[i+1][k] , dp[i][j] + abs(val[j][k]-x[i]))。
/*
* Author: chlxyd
* Created Time: 2013/7/21 13:16:22
* File Name: E.cpp
*/
#include<iostream>
#include<sstream>
#include<fstream>
#include<vector>
#include<list>
#include<deque>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cmath>
#include<ctime>
using namespace std;
const double eps(1e-8);
typedef long long lint;
#define clr(x) memset( x , 0 , sizeof(x) )
#define sz(v) ((int)(v).size())
#define rep(i, n) for (int i = 0; i < (n); ++i)
#define repf(i, a, b) for (int i = (a); i <= (b); ++i)
#define repd(i, a, b) for (int i = (a); i >= (b); --i)
#define clrs( x , y ) memset( x , y , sizeof(x) )
#define inf 1000000100
int dp[1010][130] ;
int jl[1010][130] ;
int v[130][130] ;
int a[1010] ;
int n , m , s ;
void dfs( int i , int j ) {
if ( i == 0 ) return ;
dfs( i - 1 , jl[i][j] ) ;
printf("%d" , j ) ;
if ( i == n ) printf("\n") ;
else printf(" ") ;
}
int main(){
int T;
scanf("%d" , &T ) ;
bool first = true ;
while ( scanf("%d" , &n ) == 1 ) {
if ( !first ) puts("") ;
first = false ;
repf( i , 1 , n ) scanf("%d" , &a[i] ) ;
scanf("%d %d" , &m , &s ) ;
repf( i , 0 , m - 1 )
repf( j , 0 , s - 1 ) {
scanf("%d" , &v[i][j] ) ;
}
repf( i , 1 , n )
rep( j , s ) {
dp[i][j] = inf ;
jl[i][j] = 0 ;
}
rep( i , s ) dp[1][i] = abs( a[1] - v[0][i] );
repf( i , 1 , n - 1 ) {
rep( j , s ) {
int k = j & (m-1) ;
rep( l , s ) {
if ( dp[i+1][l] > dp[i][j] + abs(a[i+1]-v[k][l]) ) {
dp[i+1][l] = dp[i][j] + abs(a[i+1]-v[k][l]) ;
jl[i+1][l] = j ;
}
}
}
}
//cout<<dp[2][1]<<endl;
int minn = inf , mem = 0;
rep( j , s ) {
if ( minn > dp[n][j] ) {
minn = dp[n][j] ;
mem = j ;
}
}
printf("%d\n" , minn ) ;
dfs( n , mem ) ;
}
}
problem F: Roads
有N个点M条边的图,每条边有权值,要求修改最少的边权值使得图的前N-1条边(这N-1条边组成的连的图是棵树)是图的最小生成树。
Solution
Tag:最小生成树,带权二分图匹配
对于前N-1条边,设为A类边,我们只会让它们的边权减少。其他的边设为B类边,只会让它们的边权值增大。对于所有A类边组成的最小生成树中,每加一条B类边都会形成一个环,对于这个环中的A类边设他权为ci,最后边权减少了li,而这条B类边权为cj,增加了lj则要有ci – li <=cj + lj,即为ci – cj <= li + lj. 然后.watashi博客中说这个是“二分图最大权匹配(Maximum WeightedMatching)的对偶问题二分图最小权覆盖(Minimum Weighted Cover)”,上网找了很久也没找到“最小权覆盖”是个啥。而我的理解是KM算法就是用由这个式子为原理来求带权匹配的(在算法执行过程中的任一时刻,对于任一条边(i,j), A[i]+B[j]>=w[i,j]始终成立)。所以我们可以建个二分图一边是A类边,一边是B类边。若两条边有连一条权威ci – cj的边,最后用Km求解。
/*
* Author: xioumu
* Created Time: 2013/7/24 15:27:37
* File Name: F.cpp
* solve: F.cpp
*/
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<string>
#include<map>
#include<set>
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
#define sz(v) ((int)(v).size())
#define rep(i, n) for (int i = 0; i < (n); ++i)
#define repf(i, a, b) for (int i = (a); i <= (b); ++i)
#define repd(i, a, b) for (int i = (a); i >= (b); --i)
#define clr(x) memset(x,0,sizeof(x))
#define clrs( x , y ) memset(x,y,sizeof(x))
#define out(x) printf(#x" %d\n", x)
#define sqr(x) ((x) * (x))
typedef long long lint;
const int maxint = -1u>>3;
const double eps = 1e-8;
const int maxn = 400 + 10;
int sgn(const double &x) { return (x > eps) - (x < -eps); }
struct Graph {
int w[maxn][maxn], lx[maxn], ly[maxn], matx[maxn], maty[maxn], n;
bool fx[maxn], fy[maxn];
void get_max(int &x, int y) {
x = max(x, y);
}
void get_min(int &x, int y) {
x = min(x, y);
}
void clear() {
memset(w, 0, sizeof(w));
n = 0;
}
void insert(int u, int v, int c) {
get_max(n, max(u + 1, v + 1));
w[u][v] = c;
}
int match() {
memset(ly, 0, sizeof(ly));
for (int i = 0; i < n; ++i) {
lx[i] = -maxint;
for (int j = 0; j < n; ++j) {
get_max(lx[i], w[i][j]);
}
}
memset(matx, -1, sizeof(matx));
memset(maty, -1, sizeof(maty));
for (int i = 0; i < n; ++i) {
memset(fx, false, sizeof(fx));
memset(fy, false, sizeof(fy));
if (!dfs(i)) {
--i;
int p = maxint;
for (int k = 0; k < n; ++k) {
if (fx[k] == true) {
for (int j = 0; j < n; ++j) {
if ((fy[j] == false)) {
get_min(p, lx[k] + ly[j] - w[k][j]);
}
}
}
}
for (int j = 0; j < n; ++j) {
ly[j] += fy[j] * p;
}
for (int k = 0; k < n; ++k) {
lx[k] -= fx[k] * p;
}
}
}
int ans = 0;
for (int i = 0; i < n; ++i) {
ans += w[maty[i]][i];
}
return ans;
}
bool dfs(int u) {
fx[u] = 1;
for (int v = 0; v < n; ++v) {
if (lx[u] + ly[v] == w[u][v] && fy[v] == false) {
fy[v] = true;
if (maty[v] == -1 || dfs(maty[v])) {
matx[u] = v;
maty[v] = u;
return true;
}
}
}
return false;
}
}G;
int n, m;
vector<int> e[maxn], d[maxn], eid[maxn], sta;
int v[maxn], cost[maxn];
bool dfs(int w, int y) {
if (w == y) return true;
if (v[w]) return false;
v[w] = 1;
rep (i, sz(e[w])) {
int j = e[w][i];
sta.push_back(eid[w][i]);
if (dfs(j, y)) return true;
sta.pop_back();
}
return false;
}
void add(int x, int y, int z, int id) {
e[x].push_back(y);
eid[x].push_back(id);
d[x].push_back(z);
}
void init() {
G.clear();
scanf("%d%d", &n, &m);
//G.set(m - n + 1, n - 1);
rep (i, n) {
e[i].clear();
eid[i].clear();
d[i].clear();
}
rep (i, n - 1) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
x--, y--;
cost[i] = z;
add(x, y, z, i);
add(y, x, z, i);
}
repf (j, n - 1, m - 1) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
x--, y--;
cost[j] = z;
sta.clear();
memset(v, 0, sizeof(v));
dfs(x, y);
rep (i, sz(sta)) {
if (cost[j] < cost[sta[i]]) {
G.insert(j - (n - 1), sta[i], abs(cost[j] - cost[sta[i]]));
}
//else G.insert(j - (n - 1), sta[i], 0);
}
}
}
void gao() {
vector<int> ans;
int h = G.match();
//printf("%d\n", h);
rep (i, n - 1)
printf("%d\n", cost[i] - abs(G.ly[i]), G.ly[i]);
repf (i, n - 1, m - 1)
printf("%d\n", cost[i] + abs(G.lx[i - (n - 1)]), G.lx[i - (n - 1)]);
}
int main() {
int T;
scanf("%d", &T);
rep (ca, T) {
if (ca != 0) puts("");
init();
gao();
}
return 0;
}
Problem G: Robbers
一群海盗劫了Y块钱,每人分了Xi块。后来又劫了M块钱,每个人分Ki块。问要如何分配Ki能使所有|Ki/M – Xi/Y| 的和最小。
Solution
Tag:贪心
枚举每一块钱。对于每一块钱,枚举分配给谁,记分配这块钱之前与Xi/Y的差距和分配之后与Xi/Y的差距的差为Di,这个Di表示分配给他后|Ki/M – Xi/Y| 的和会减少多少或增加多少,找到最大的Di的人,把这块钱分配给他。
/*
* Author: chlxyd
* Created Time: 2013/7/20 13:11:33
* File Name: G.cpp
*/
#include<iostream>
#include<sstream>
#include<fstream>
#include<vector>
#include<list>
#include<deque>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cmath>
#include<ctime>
using namespace std;
const double eps(1e-8);
typedef long long lint;
#define clr(x) memset( x , 0 , sizeof(x) )
#define sz(v) ((int)(v).size())
#define rep(i, n) for (int i = 0; i < (n); ++i)
#define repf(i, a, b) for (int i = (a); i <= (b); ++i)
#define repd(i, a, b) for (int i = (a); i >= (b); --i)
#define clrs( x , y ) memset( x , y , sizeof(x) )
const int maxn = 1000 + 10;
double v[maxn];
int now[maxn];
int a[maxn];
int n, m, y;
int sgn(double x) {
return (x > eps) - (x < -eps);
}
int main(){
int T;
scanf("%d", &T);
rep (ca, T) {
if (ca != 0) puts("");
scanf("%d%d%d", &n, &m, &y);
rep (i, n) {
scanf("%d", &a[i]);
v[i] = 1.0 * a[i] / y;
}
memset(now, 0, sizeof(now));
rep (i, m) {
double mi;
int id = -1;
rep (j, n) {
double old = abs(1.0 * now[j] / m - v[j]);
double ne = abs(1.0 * (now[j] + 1) / m - v[j]);
double dif = ne - old;
if (id == -1 || sgn(mi - dif) > 0) {
id = j;
mi = dif;
}
}
now[id]++;
}
rep (i, n) {
if (i != 0) printf(" ");
printf("%d", now[i]);
}
printf("\n");
}
return 0;
}
Problem H: Toral Tickets
一张有N*M的方格纸,每个方格可以染白色或者黑色,可以先卷成圆柱后在卷成一个游泳圈状。求不同的染红方案数
Solution
Tag:波利亚计数定理
相当于方格可以一整行位移和一整列位移,可以旋转。然后直接用波利亚计数定理算就行了。
/*
* Author: xioumu
* Created Time: 2013/7/26 21:26:22
* File Name: H.cpp
* solve: H.cpp
*/
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<string>
#include<map>
#include<set>
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
#define sz(v) ((int)(v).size())
#define rep(i, n) for (int i = 0; i < (n); ++i)
#define repf(i, a, b) for (int i = (a); i <= (b); ++i)
#define repd(i, a, b) for (int i = (a); i >= (b); --i)
#define clr(x) memset(x,0,sizeof(x))
#define clrs( x , y ) memset(x,y,sizeof(x))
#define out(x) printf(#x" %d\n", x)
#define sqr(x) ((x) * (x))
typedef long long lint;
const int maxint = -1u>>1;
const double eps = 1e-8;
const int maxn = 20 + 10;
int sgn(const double &x) { return (x > eps) - (x < -eps); }
int n, m;
int a[maxn][maxn];
int ch1[maxn * maxn], ch2[maxn * maxn], ch3[maxn * maxn];
int fa[maxn * maxn], v[maxn * maxn], sum[maxn * maxn];
int find(int w) {
if (fa[w] == w) return w;
int k = find(fa[w]);
fa[w] = k;
return k;
}
void rotate(int a[maxn][maxn], int n, int m) {
int b[maxn][maxn];
memcpy(b, a, sizeof(b));
rep (i, n)
rep (j, m) {
a[i][j] = b[j][n - i - 1];
}
}
void makeCh(int a[maxn][maxn], int b[maxn][maxn]) {
rep (i, n)
rep (j, m) {
int r = find(a[i][j]);
int w = find(b[i][j]);
if (r != w) {
if (r > w) swap(r, w);
fa[w] = r;
sum[r] += sum[w];
}
}
}
void getChange() {
int cnt = 0;
int b[maxn][maxn];
rep (i, n * m) {
fa[i] = i;
sum[i] = 1;
}
rep (i, n) {
rep (j, m) {
a[i][j] = cnt++;
}
}
memcpy(b, a, sizeof(a));
rep (i, n - 1) {
rep (j, m) {
swap(b[i][j], b[i + 1][j]);
}
}
makeCh(a, b);
memcpy(b, a, sizeof(a));
rep (j, m - 1)
rep (i, n) {
swap(b[i][j], b[i][j + 1]);
}
makeCh(a, b);
memcpy(b, a, sizeof(a));
rotate(b, n, m);
if (n != m) {
rotate(b, m, n);
}
makeCh(a, b);
}
void gao() {
int gn = 0;
int ans = 0;
memset(v, 0, sizeof(v));
rep (i, n * m) {
int res = 0;
int r = find(i);
if (v[r] == 0) {
v[r] = 1;
ans += pow(2, sum[r]);
gn++;
}
}
ans /= gn;
printf("%d\n", gn);
printf("%d\n", ans);
}
int main() {
while (scanf("%d%d", &n, &m) == 2) {
if (m > n) swap(n, m);
getChange();
gao();
}
return 0;
}