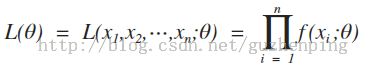数学篇----参数估计之最大似然估计法[概率论]

前言

    参数估计问题分：点估计、区间估计。

    点估计是适当地选择一个统计量作为未知参数的估计（称为估计量），若已取得一样本，将样本值代入估计量，得到估计量的值，以估计量的值作为未知参数的近似值（称为估计值）。（另一种解释：依据样本估计总体分布中所含的未知参数或未知参数的函数。）

    有很多求点估计的方法：最大似然估计法、矩估计法、最小二乘法、贝叶斯估计法。重点就是最大似然法。

    最大似然估计法的基本思想：若已观察到样本（X1，X2，··· ，Xn）的样本值（x1,x2,...,xn），而取得这一样本值得概率为p（在离散型的情况），或（X1，X2，··· ，Xn）落在这一样本值（x1,x2,...,xn）的邻域内的概率为p（在连续型的情况），而p与未知参数有关，我们就取θ的估计值使概率p取得最大。

    说说区间估计，因为点估计不能反映估计的精度，所有才用。

1 基本概念

似然：可以理解为“可能性”，这样就有“概率”的意思了。

符号：θ可能取值的范围。

符号：在不致混淆的情况下统称估计量和估计值为估计，记为。

估计量：

估计值：

注：（X1，X2，··· ，Xn）是一个样本，（x1,x2,...,xn）是相应的样本值。

概念如下图：

2 为什么叫“最大”

    费希尔（R.A.Fisher）的想法：固定样本观察值x1,x2,...,xn，在θ取值的可能范围内挑选使似然函数L(x1,x2,...,xn;θ)达到最大的参数，作为参数θ的估计值。即取使：

                   

    为了使似然函数的结果最大，所选的参数θ一定也要大，记为。这个被称为最大似然估计（不单单是估计了），其中是参数θ的最大似然估计值，是参数θ的最大似然估计量。

3 求解过程

    会遇到两类求解：总体X是连续型，总体X是离散型。但是差不多，连续型的求解可以变成离散型的。

    已知条件：总体X属连续型，概率密度 f(x;θ)，θ∈。

    设X1，X2，··· ，Xn是来自X的一个样本，则X1，X2，··· ，Xn的联合密度为：

                                             

   

    设x1,x2, ... ,xn是相应于样本X1，X2，··· ，Xn的一个样本值，则随机点（X1，X2，··· ，Xn）落在点（x1,x2, ... ,xn）的领域内的概率近似地为：

                                             ，其值随θ的取值而变化。

   

    与离散型的情况一样，我们取θ的估计值使概率取得最大值，但因子不随θ而改变，故只需考虑函数：

                                           的最大值。这里L(θ)称为样本的似然函数。

   

  

    若，

则称为θ的最大似然估计值，称为θ的最大似然估计量。

====================分割性===================================分割性====================================分割性=====================

   

    到这，确定最大似然估计量的问题就归结为微分学中的求最大值问题。

    若 f(x;θ) 关于θ可微，这时可以从下面的方程解得：

                          

    因为L(θ)与 lnL(θ) 在同一θ处取得极值，因此，θ的最大似然估计θ也可以从下面的方程解得:

                          ，这个叫对数似然方程。

 （我也不太懂大牛们为什么取对数求解，需要学习。）

附：

其他同学的总结，最大似然估计法的一般步骤：

• 写出似然函数；
• 对似然函数取对数，并整理；
• 求导数；
• 解似然方程。

参考资料：《概率论与数理统计（第四版）》  浙江大学  盛骤 谢式千 潘承毅 编

内容来自：谷震平的博客，希望尊重版权，尊重原创。

链接：http://blog.csdn.net/guzhenping