scheme序对与表的进阶
在上一篇博客中介绍了序对与表的内在关系,蜻蜓点水,只涉及了点皮毛。因为这两个概念的重要性,有必要再深入的理解,所以继续思考SICP中涉及这两个概念的地方。
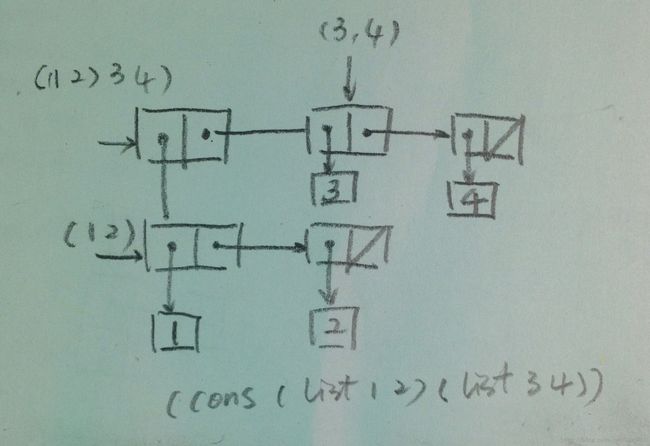
已知表是由序对构造而成,同时表和序对都满足闭包特性。上一篇中已经给出了表'((1 2) 3 4)是由(cons (list 1 2) (list 3 4))。那么(list (list 1 2) (list 3 4))是哪样呢?与(cons (list 1 2) (list 3 4))有哪样区别呢?
左图表示的是(list (list 1 2) (list 3 4)),右图表示的是(cons (list 1 2) (list 3 4))。所以当用cdr分别求上面两个值时,得出的结果分别是'((3 4))和'(3 4)。scheme语言的本身就是用list表示的,例如上面的语句(list 1 2)在解释器内部就是一个表,表的三个元素分别是list、1和2。对它们分别求值,数字1、2的值是数字本身,而scheme约定表括号内的第一个元素是操作符,操作对象就是后面其他的元素,在这里就是1和2。所以这个式子的求值结果就是有list操作符作用在1和2上,产生包含元素1和2的表,用'( 1 2 )表示。(list (list 1 2) (list 3 4))根据表的闭包特性,表操作符的操作对象可以是另一个表(此表的值也通过子表达(list x x)求值得到),这里就是将表'(1 2)和'(3 4)作为元素再生成表'((1 2) (3 4))。到这里看以看到“数据”和“代码”其实是一回事,看你从哪个角度去看,也进一步说明“递归”是程序的本质特性之一。
用树结构来表示上述两个表,更加形象,尤其涉及到递归操作时。
每一个非叶子节点代表一个表,左图有三个表组成,右图两个表。