【连通性状态压缩DP】poj1739
极其恶心的一道状态压缩dp,很多细节的地方想得我头昏脑胀,做这道题差不多花了整整一天的时间吧(调到凌晨6.00),想啊想,草稿纸都花了几十张,方法和标准做法有点不一样,和cdq2008年论文中提到的方法差不多。
首先这道题是要我们求从一个图的左下角至右下角的哈密顿路径的条数,因为起点和终点确定了,所以可以转化为求哈密顿回路,默认左下角和右下角的方块已经连通就可以了。
关于状态的设计也是参考cdq2008年论文里介绍的‘插头’和‘轮廓线’的方法:
轮廓线的定义就是已决策方格和未决策方格的分割线,然后我们按照从左到右,从上到下的方法进行DP,那么这一条轮廓线的长度肯定是小于等于m+1的。
插头分为左插头和右插头,其中左插头和右插头两两匹配,类似于括号序列由此我们便可以用三进制(1表示左插头,2表示右插头,0表示无插头)的方法进行状态压缩。
转移一共有6种转移:
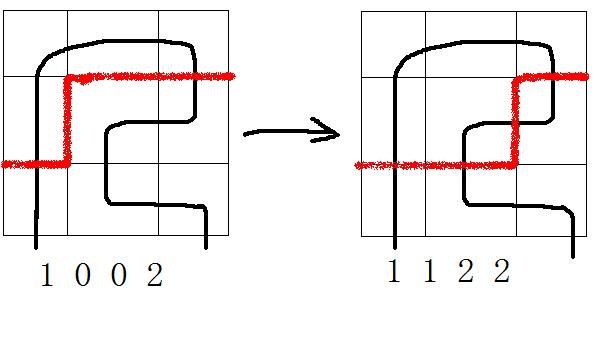
1.这个方格上面没有插头,那么也就是意味着路径在这里打了个弯,因此生成一左一右两个插头:
2.这个方格上方或左方有一个插头,那么他可以继续延续,插在下方或者是右方:
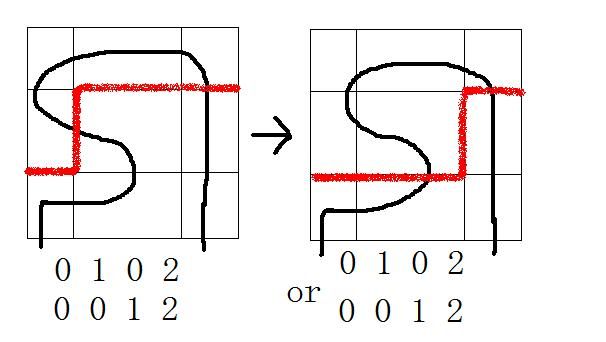
3.这个方格上有一右一左两个插头,直接删除合并:
4.这个方格上游一左一右两个插头,直接pass,因为用他转移的话路径将会出现不连通的环;
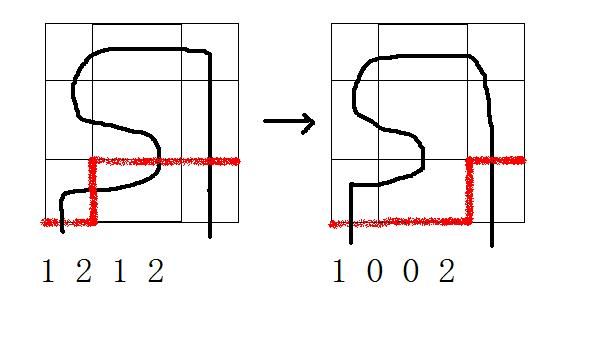
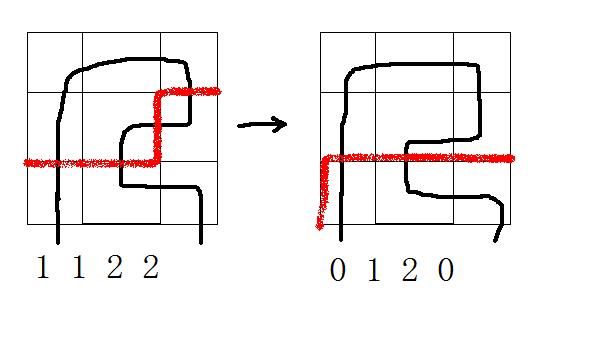
5.这个方格上有两个左插头,同样意味着路径在这里打了个弯,我们需要把这两个左插头删掉,并且把较靠右的左插头所匹配的右插头改成左插头(开始想成把右边第一个右插头删掉,无限WA。。):
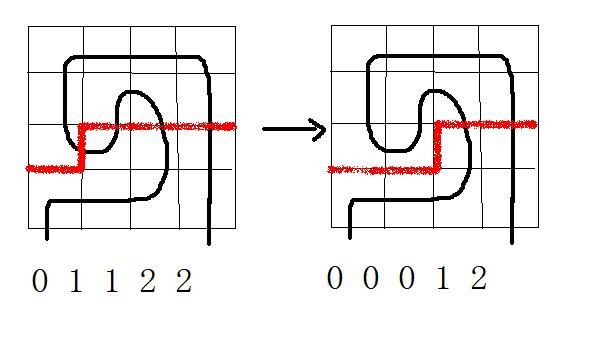
6.这个方格上有两个右插头,同上:
原题是多组数据,所以把所有状态预处理出来比较好,8*8的极限数据也只扩展出千把个状态。
哎,这次程序又写丑了,才跑个800MS,倒数第几。。。看来还是不能偷懒,要写预处理(貌似在一个很大的数组里面来回寻址很耗时间)。
奇丑无比的代码:
program poj1739; var f,q:array[0..1,0..265000] of longint; h:array[0..265000] of boolean; i,j,k,max,n,m,o,t:longint; map:array[0..8,0..8] of char; procedure update(a,b:longint); begin if j=m then if b<=max then b:=b<<2 else exit; t:=o xor 1; inc(f[t][b],a); if not h[b] then begin inc(q[t][0]); q[t][q[t][0]]:=b; h[b]:=true; end; end; procedure work(st,ff:longint); var w1,w2,s1,s2,k,z:longint; begin w1:=2*j-2;w2:=2*j; s1:=(st>>w1)and 3; s2:=(st>>w2)and 3; k:=st xor (s1<<w1) xor (s2<<w2); z:=1; if map[i,j]='#' then begin if (s1=0)and(s2=0)then update(ff,st); exit; end; if (s1=0)and(s2=0) then update(ff,k+(1<<w1)+(2<<w2)) else if s1=0 then begin update(ff,k+(s2<<w1)); update(ff,k+(s2<<w2)); end else if s2=0 then begin update(ff,k+(s1<<w1)); update(ff,k+(s1<<w2)); end else if (s1=1)and(s2=1)then begin repeat inc(w2,2); t:=(st>>w2)and 3; if t=1 then inc(z); if t=2 then dec(z); until z=0; update(ff,k xor (3<<w2)); end else if (s1=2)and(s2=2)then begin repeat dec(w1,2); t:=(st>>w1)and 3; if t=2 then inc(z); if t=1 then dec(z); until z=0; update(ff,k xor (3<<w1)); end else if (s1=2)and(s2=1)then update(ff,k); end; begin readln(n,m); while (n<>0)or(m<>0) do begin for i:=1 to n do begin for j:=1 to m do read(map[i,j]); readln; end; o:=0; q[0,0]:=1;q[0,1]:=0; f[0,0]:=1;max:=(1<<(2*m))-1; for i:=1 to n do for j:=1 to m do begin for k:=1 to q[o,0] do work(q[o,k],f[o,q[o,k]]); fillchar(h,sizeof(h),false); fillchar(f[o],sizeof(f[o]),0); q[o,0]:=0;o:=o xor 1; end; writeln(f[o,(1<<2)+(2<<(2*m))]); fillchar(f,sizeof(f),0); fillchar(q,sizeof(q),0); readln(n,m); end; end.