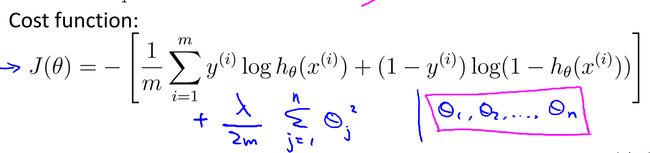斯坦福机器学习公开课笔记(四)--规格化

公开课地址：https://class.coursera.org/ml-003/class/index 

授课老师：Andrew Ng

1、the problem of overfitting(过拟合的问题)

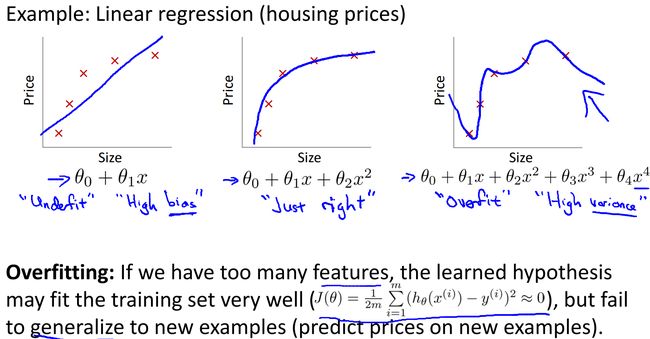
回到我们最早提到的预测房屋价格与房屋面积关系的线性回归问题，最简单的模型是线性关系，但是在很多情况下线性关系是不适用的，需要引入二阶三阶等。不过在引入高阶后又存在新的问题，样本数据能很好的拟合了，但是对于新来的数据却不能保证正确性，这就很可能出现了所说的过拟合：

从上图可以看到，左侧线性拟合效果很差，存在较大的偏差值，右侧函数的阶数明显过高，存在较大的方差值，只有中间的二阶函数才是比较正确的结果。我们也可以判断从右侧的函数走向预测正确的可能性很低，而中间函数的走向能看到规律性，预测正确的可能性很大。与此相似的是，在逻辑回归中也存在过拟合的问题，如下图所示：

那么怎么解决过拟合问题呢？存在以下几种方法：

上面列出的一个是减少特征的数目，可以通过人工决定要剩下多少特征或者是让算法去决定，另一个是规格化，我们可以留下所有的特征，但要让函数式子中参数theta值尽量小。这样的目的是尽量让函数项最少，所有theta都取0才好。具体内容下面会细讲。

2、cost function(代价函数)

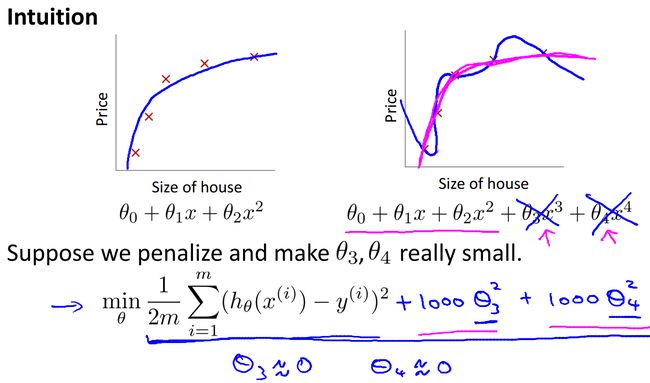
依然是逃不掉的代价函数，既然我们在上面提到让theta值尽可能小，那么需要对代价函数进行修改。

如上图所示，我们在代价函数里面增加了高阶项系数theta3和theta4额外两项，这两项对整个代价函数影响很大，求解时不难想到这两个系数的取值会尽量接近于0，函数中高阶项也因此趋近0. 我们写成更一般的形式，注意后面不含theta0这一项：

和线性回归相比，后面增加了一项，这就是规格化后的代价函数。这里lambda的意思是规格化参数，这个取值是自己设定的，当lambda取值过小对防止过拟合意义不大，不能保证theta们尽量取0，当取值过大时，就会存在下面的问题：

虽然不存在过拟合了，但是变成了欠拟合，房屋售价预测变成下面这样：

这种取值固定的函数显然就没什么意义了。

3、regularized linear regression(规格化线性回归)

代价函数改变了，梯度下降也自然要改变，除了theta0以外，其余的theta要多减去一项：

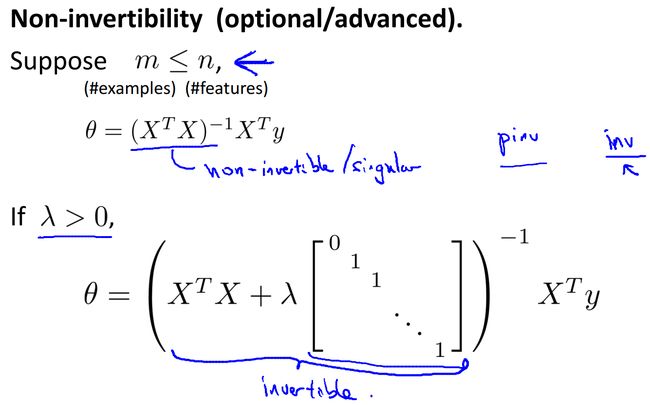
如果不用梯度下降而采用正规化等式进行计算，让J对theta的导数全为0，可以求出theta（这里省略推导过程）：

容易知道括号内的矩阵和满秩，故一定可逆。

4、regularized logistic regression(规格化逻辑回归)

逻辑回归的规格化和线性回归的规格化类似，也是先修改代价函数：

然后修改梯度下降的过程：

-------------------------------------弱弱的分割线----------------------------------

所谓规格化就是为了防止过拟合而采取的一种方法，通过加入对参数的惩罚项来让参数的取值尽可能的小，从而让函数中不存在那么多高阶的函数项。不过，对于规格化系数也就是惩罚系数的选择是这个方法中需要注意的问题，这种选择和梯度下降中的系数类似，过大过小都不好。