A*算法

关于A*算法实用性优化的个人想法

　　这里的A*优化只是针对网上一些关于A*算法介绍的文章来写的，至于我接触过的A*代码可能都算不上专业级别因此我从这些代码开始优化也只是觉得这些代码的优点在于说明算法，而在效率与实用性方面就有些欠缺。

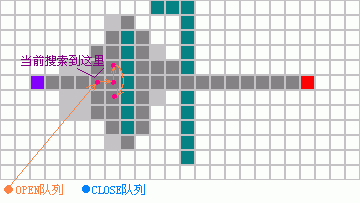
　　A*是启发试搜索加动态规划。具体实现依靠两个队列Open队列和Close队列。从一点开始探走几个相邻的格子如果可以移动且当前移动为起点到哪个格子的历史最佳方法则把那个格子按照估价值从小到大插入Open队列里面，几个方向试探结素后取出估价值最小的节点放入Close再从这里开始试探几个相邻的方向同样放入Open队列里面，放入Open的条件是1.这步在地图上面是可以移动的，2.这步所在节点在Open里面并不存在，3.从起点到这步的实际距离比这点的历史最小距离还短满足这三个条件就把节点放入Open队列。具体的算法网友们已经描述的再清楚不过了大致算法如下:

findpath() { 　把S点加入Open队列（按该点到E点的距离排序+走过的步数从小到大排序） 　1、排序队列Open队列中距离最小的第一个点出列，并保存入Close队列中 　2、从出列的点出发，分别向4个（或8个）方向中的一个各走出一步 　3、并估算第2步所走到位置到目标点的距离，并把该位置按估价距离从小到大排序后并放入Open队列中 　4、如果该点从四个方向上都不能移动，则把该点从Close队列中删除 　5、回到第一点，直到找到E点则结束 　从目标点回溯树，直到树根则可以找到最佳路径，并保存在path[]中 }

具体实现和详细算法可以看这段代码(sort_queue和store_queue是open和close队列)

　　我觉得要使它可以胜任即时战略游戏第一点要改的就是规定搜寻的规模，即限制close_queue的大小，一旦超过大小而并没有到达终点，则取一个搜寻过的最接近终点的点(从它到终点的估价距离最短)作为搜索的终点。二一旦Open队列空了无法取出节点时搜索结束没有找到终点，此时还是按照上面的方法找一个最接近终点的点代替终点。

　　
　　这样搜索就不会漫无边际地进行下去了。上面的程序大家稍微观察就会发现几处影响速度的致命地方，启发试搜索是不变的，而看程序每次加入取出两个队列时都要进行繁琐的内存分配，这是项耗费时间的工作，其次需要检查是否在队列中，这点也是很慢的，最后就是保存动态规划数据(历史最短距离)的数组进行还原，并且每次寻路都要还原若大的数组，这是无法接受的。

　　我所说的优化是从数据结构入手解决上面的问题让Open/Close两队列处理时不再涉及内存分配问题，首先建立一个与地图上面每个节点一一对应的节点数组Node[maph][mapw];Node里面有一个指针Next和Father，Next指相所在队列的下一个节点，Father指向它的父节点。由于Open/Close两队列不可能出现一个节点在某个队列同时出现两次的情况因此Open队列描述时只要让它指向一个节点地址&Node[y][x]然后让Node[y][x]的Next指向队列下一个节点，如果没有节点则这点的Next为NULL，同样的道理Close也是这样描述的如此来看每次搜寻的时候就不必内存分配了，插入节点(x,y)时只要改动Node[maph][mapw]上面的数据和Open/Close两个指针就轻松搞定了见程序的AddToOpenQueue等几个函数。在初始化的时候一次性分配**Node为Node[maph][mapw](TAstarNode的定义如下表)Open/Close为两个TAstarNode指针以后就不再分配内存了，初始化让Open/Close都等于NULL在Open中加入节点(x,y)就按照普通连表的方法插入&Node[y][x]换而言之，就是让Open/Close指向Node[maph][mapw]中的某个元素，然后这个元素又指向下一个元素形成链表，由于算法中每次加入Open/Close的节点前检查如果存在了就不再加入因此Open/Close不会有重复的元素。

struct TAstarNode { 　ADWORD Pos;　　　　　// ((y<<16)|x)初始化时设定以后不变 　short ActualCost;　　// 保存从起点到该节点的实际开销 　short EstimateCost;　// 保存此点的估价开销由JudgeCost函数提供初始化为MAX 　short SumCost; 　　　// 前面两者的和，用于插入排序 　TAstarNode *Father;　// 此点的父节点 　TAstarNode *Prev;　　// 在Open或者Next链表的上一个节点用来方便从两队列中删除 　TAstarNode *Next;　　// 在Open或者Next链表中的下一个节点 　char Modified;　　　 // 1位该节点是否被修改过，2/3位代表是否于Open/Close表 } **Node,*Open,*Close; // Node[maph][mapw]和Open/Close队列

右图为Node[h][w]和Open表的示范，初始化Node时设置EstimateCost为MAX另外需要一个变量描述改动状态(Modified)，如果改动过最佳记录则状态第0位为1，如果在Open队列中则地1位为1，如果在Close中则第2位为1那么只要通过位运算就可以知道节点和队列的关系了，另外用一个数组来记录修改过最佳距离的节点位置，并且依据前面的状态变量来判断如果以前已经记录过就不再记录了，当路径搜索完以后就根据这个数组来还原数据了。 　　请看右边的搜索试列图，可以简单看出OPEN队列在插入/删除时并不需要内存分配而只要改变其指针和Node[h][w]中节点的Next指针就行了。这是激动人心的提高，

　　

　　我们首先加入了搜索限制其次除去了内存分配，再者把每次查找一个节点是否在Open/Close链表中从搜索链表化简成检查标志，路径算法已经省去了许多不必要的工序了，再看下实用性方面，首先判断地图是否可以移动不要在算法中直接判断而最好设置一个虚函数MoveAble(x,y)来实现(程序中我用函数指针代替)，因为在游戏中某块地图对于地面单位和空中单位还有水下单位可以移动的情况都不同因此直接操作地图元素并不是明智的选择，再者估价函数JudgeCost(x,y)也应该设置成虚函数或者函数指针来实现，毕竟求估价值的方法很灵活，这里不能限制死了。

　　还有每次寻路搜索哪些方向呢？用DirMask来描述0-7位代表从上开始顺时针一圈的八个方向情况，0代表不搜索，1代表搜索，那么四个方向搜索可以用0x55(1010101b)来代替，八个方向可以用0xff来设定，如此一来你可以设定只进行搜索3个方向的寻路，这样可以满足一些简单的寻路任务了，比如RPG中NPC敌人的移动就可以这样来设定。最后就是范围问题的设定了，Open表的最大大小可以设置为100-200(四个方向)或200-300(八个方向)而Close表的大小即处理节点的最多数目可以设置成(MapH*MapW)/16这样的设定在士兵走入一个桶形地形时并不会花费很大的开销去寻找通路，而是走到桶形地形的尖端。其具体值可以适当调整，当然数值越大搜索就越广，开销也就越大(MapH*Map)/16这个数值我自己感觉比较接近星际的寻路特点

　　其它优化，由于Open队列中的数据全部是连表插入排序的，当数据多时效率并不会见得高。这时如果还要继续优化手段也很多，比如建立Hash散列表，或者用二叉树来代替连表排序，大家可以参考前导公司的写的A*代码里面就用了散列表这点很优秀，但它任然摆脱不了大量的内存分配/释放。因此此处我觉得不怎么高明。

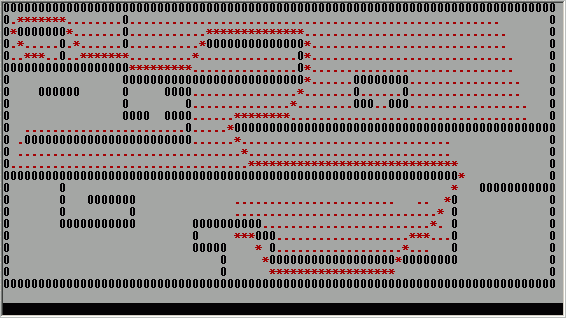
　　到是估价值的计算方法很多，但是写的好坏也关系到搜索的规模：坐标差之绝对值乘加权值求和，平方和开方还有些怪的呢，可以看看前导的代码估价函数是怎么写的。我看到网上有文章说当前节点到终点的估计距离不能比实际距离大，说什么才能叫做A*算法，否则只能叫A算法(人工智能书上说的)，因为不一定是最短路径，呵呵但是如果只是满足估价值小于真实值也不一定就可以找到最短路径故暂且不论，先看JudgeCost的意义--使搜索更靠近终点，势必减小JudgeCost将会增加搜索的宽度及规模，增加JudgeCost则使搜索跟快地向终点靠拢。下面是使用不同估价函数的对比：

JudgeCost=abs(dx)+abs(dy)	JudgeCost=abs(dx),abs(dy)加权求和

　　上图两种估价函数的求法，星号是路径点是搜索过的节点，当JudgeCost大于真实值时从一个节点出发算法更愿意搜索一个靠终点近的点，换言之JudgeCost越大算法就越买力向终点靠拢，从左右两副图可以清楚看到(点击放大)。所以我们使用坐标差加权求和来处理或者直接求和乘与一个数字(比如8)在地形复杂的时候就更加显出这种方法的实用性了，良种式子的规模差距还要比上图严重的多。所以通用地用加权求和dx=abs(x-endx),dy=abs(y-endy);if (dx>dy) result =10*dx+6*dy; else result=10*dy+6*dx;就是这个意思，所用的乘10和乘6是试验证明比较好用的数字了，如此一来搜索的规模就被控制得又减小了，是不可忽视的。这里有例子程序，可以测试搜索规模等。

　　还有几点要注意的，集体寻路要采用跟随政策，共用一条路径，中途遇到移动物分三步走：尝试加入一个斜方的路径节点看是否可以饶过;不能就等待移动物体自己走开;到了时间不走再另外搜寻路径，大场景要预先设定一些路径节点中转站再进行远距离搜索时可以大大提高效率，用方向保存路径比用坐标保存节省至少1/4的空间。。。。碰到敌人部队就开枪，自己部队则可以不走了，或者发送两条指令给挡住路的士兵的指令队列1.移开当前位置并等待;2.回到当前位置，这样可以产生一个一个顺序让路的精彩效果，红警里面早已有实现:-)

　　讲远了，那是行军问题了，前段时间给一个高中生辅导NOI复赛，那小子竟然在讲到广度优先时问了路径算法，一时兴起就写了这篇文章以及一段三百多行的程序，顺便供大家参考:-)　一家之言，欢迎来信讨论: [email protected]