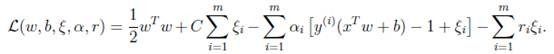斯坦福大学公开课 :机器学习课程(Andrew Ng)——7、监督学习:Support Vector Machine,立
10)规则化和不可分割情况(Regularization and the non-separable case)
11)坐标上升法(Coordinate ascent)
12)SMO优化算法(Sequential minimal optimization)
12.1)SMO算法
12.2)SMO算法中拉格朗日乘子的启发式选择方法
13)总结
10)规则化和不可分割情况(Regularization and the non-separable case)
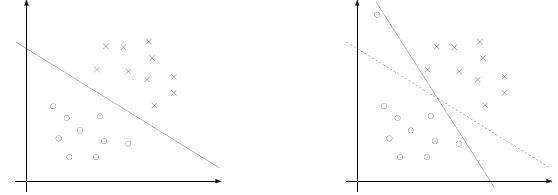
之前的讨论都是建立在样例线性可分的假设上,当样例线性不可分时,我们可以尝试使用核函数将特征映射到高维,这样很可能就可分了。然而,映射后我们也不能100%保证可分。这时候我们应该允许一些点游离并在模型中违背限制条件(函数间隔大于1)。对应下面两幅图,我们更希望得到第一幅而不是第二幅:
因此,我们设计新模型如下(也称软间隔):
引入非负参数![]() 后(称为松弛变量),就允许某些样本点的函数间隔小于1(即,不像之前严格大于等于1),甚至在最大间隔区间里面函数间隔是负数,即个别样本点甚至可以在相反分类的区域中。而放松限制条件后,我们需要重新调整目标函数,以对离群点进行处罚,目标函数后面加上的
后(称为松弛变量),就允许某些样本点的函数间隔小于1(即,不像之前严格大于等于1),甚至在最大间隔区间里面函数间隔是负数,即个别样本点甚至可以在相反分类的区域中。而放松限制条件后,我们需要重新调整目标函数,以对离群点进行处罚,目标函数后面加上的![]() 就表示离群点越多,目标函数值越大,而我们要求的是尽可能小的目标函数值。这里的C是离群点的权重,C越大表明离群点对目标函数影响越大,也就是越不希望看到离群点。我们看到,目标函数控制了离群点的数目和程度,使大部分样本点仍然遵守限制条件。
就表示离群点越多,目标函数值越大,而我们要求的是尽可能小的目标函数值。这里的C是离群点的权重,C越大表明离群点对目标函数影响越大,也就是越不希望看到离群点。我们看到,目标函数控制了离群点的数目和程度,使大部分样本点仍然遵守限制条件。
此模型修改后,引起下面一些东西的变化:
a)拉格朗日公式改变如下:
b)利用和上一节类似的推导过程,得出极值的改变结果如下:
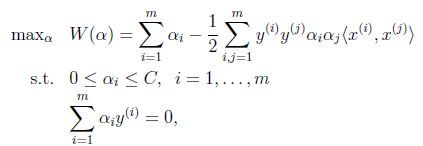 ,我们发现没有了参数
,我们发现没有了参数![]() ,与之前模型唯一不同在于
,与之前模型唯一不同在于![]() 又多了
又多了![]() 的限制条件。
的限制条件。
c)KKT条件的变化如下:
第一个式子表明在两条间隔线外的样本点前面的系数为0,第二个式子表明离群样本点前面的系数为C,第三个式子表明支持向量(也就是在超平面两边的最大间隔线上的)样本点前面的系数在(0,C)之间。通过KKT条件可知,某些在最大间隔线上的样本点也不是支持向量,相反也可能是离群点。
d)b*的求值公式也发生了改变,改变结果在SMO算法里面介绍。
11)坐标上升法(Coordinate ascent)
在讨论极值![]() 的求解之前,我们先看看坐标上升法的基本原理。
的求解之前,我们先看看坐标上升法的基本原理。
假设要求解下面的优化问题:![]() ,这里W是
,这里W是![]() 向量的函数。之前我们在回归中提到过两种求最优解的方法,一种是梯度下降法,另外一种是牛顿法。现在我们再讲一种方法称为坐标上升法(求解最小值问题时,称作坐标下降法,原理一样)。
向量的函数。之前我们在回归中提到过两种求最优解的方法,一种是梯度下降法,另外一种是牛顿法。现在我们再讲一种方法称为坐标上升法(求解最小值问题时,称作坐标下降法,原理一样)。
方法过程:
最里面语句的意思是固定除![]() 之外的所有
之外的所有![]() ,这时W可看作只是关于
,这时W可看作只是关于![]() 的函数,那么直接对
的函数,那么直接对![]() 求导优化即可。这里我们进行最大化求导的顺序i是从1到m,可以通过更改优化顺序来使W能够更快地增加并收敛。如果W在内循环中能够很快地达到最优,那么坐标上升法会是一个很高效的求极值方法。
求导优化即可。这里我们进行最大化求导的顺序i是从1到m,可以通过更改优化顺序来使W能够更快地增加并收敛。如果W在内循环中能够很快地达到最优,那么坐标上升法会是一个很高效的求极值方法。
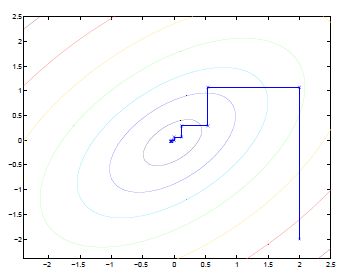
下面通过一张图来展示:
椭圆代表了二次函数的各个等高线,变量数有2个,对应x、y坐标轴。起始坐标是(2,-2),图中的直线是迭代优化的路径,可以看到每一步都会向最优值前进一步,而且前进路线是平行于坐标轴的,因为每一步只优化一个变量。
12)SMO优化算法(Sequential minimal optimization)
SMO算法几乎是最快的二次规划优化算法,特别针对线性SVM和数据稀疏时性能更优。
12.1)SMO算法
在上面的某一节中提到,α*的求解要交给SMO算法,下面我们就针对对偶函数的优化问题进行讲解:
要解决的是在参数![]() 上求最大值W的问题,至于
上求最大值W的问题,至于![]() 和
和![]() 都是已知数。C由我们预先设定,也是已知数。
都是已知数。C由我们预先设定,也是已知数。
与坐标上升的思路不同的是,由于问题中规定: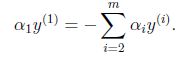 ,我们需要一次选取两个参数做优化(想一想为什么)。假如我们选择
,我们需要一次选取两个参数做优化(想一想为什么)。假如我们选择![]() 和
和![]() 这两个参数,有下面的等式限制:
这两个参数,有下面的等式限制:
 ,由于
,由于![]() 都是已知固定值,因此为了方面,可将等式右边标记成实数值
都是已知固定值,因此为了方面,可将等式右边标记成实数值![]() ,即:
,即:![]() 。
。
当![]() 和
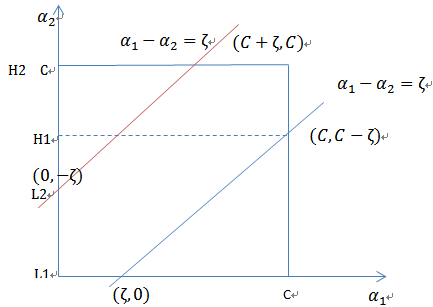
和![]() 异号时,也就是一个为1,另一个为-1时,他们可以表示成一条直线,斜率为1。如下图:
异号时,也就是一个为1,另一个为-1时,他们可以表示成一条直线,斜率为1。如下图:
![]() ,展开后W可以表示成
,展开后W可以表示成![]() 。其中a,b,c是常量参数。这样,通过对W进行求导可以得到
。其中a,b,c是常量参数。这样,通过对W进行求导可以得到![]() ,然而要保证
,然而要保证![]() 满足
满足![]() ,我们使用
,我们使用![]() 表示求导求出来的
表示求导求出来的![]() ,然而最后的
,然而最后的![]() ,要根据下面情况得到:
,要根据下面情况得到:
这样得到![]() 后,我们可以得到
后,我们可以得到![]() 的新值
的新值![]() 。 至此,α*求出后,就可以根据上一节讲的内容求w和b了。
。 至此,α*求出后,就可以根据上一节讲的内容求w和b了。
意思是,第一步选取一对![]() 和
和![]() ,选取方法使用启发式方法(后面讲)。第二步,固定除
,选取方法使用启发式方法(后面讲)。第二步,固定除![]() 和
和![]() 之外的其他参数,确定W极值条件下的
之外的其他参数,确定W极值条件下的![]() ,
,![]() 由
由![]() 表示。
表示。
SMO之所以高效就是因为在固定其他参数后,对一个参数优化过程很高效。
12.2)SMO算法中拉格朗日乘子的启发式选择方法
选择第一个拉格朗日乘子用的启发式选择方法主要思想是:每次选择拉格朗日乘子的时候,优先选择样本前面系数![]() 的
的![]() 作优化(论文中称为无界样例),因为在界上(
作优化(论文中称为无界样例),因为在界上(![]() 为0或C)的样例对应的系数
为0或C)的样例对应的系数![]() 一般不会更改。
一般不会更改。
选择第二个拉格朗日乘子用的启发式选择方法主要思想是:第二个乘子的迭代步长大致正比于![]() ,选择第二个乘子能够最大化
,选择第二个乘子能够最大化![]() ,即当
,即当![]() 为正时选择负的绝对值最大的
为正时选择负的绝对值最大的![]() ,反之,选择正值最大的
,反之,选择正值最大的![]() 。
。
最后的收敛条件是在界内(![]() )的样例都能够遵循KKT条件,且其对应的
)的样例都能够遵循KKT条件,且其对应的![]() 只在极小的范围内变动。至于如何写具体的程序,请参考John C. Platt在论文中给出的伪代码。
只在极小的范围内变动。至于如何写具体的程序,请参考John C. Platt在论文中给出的伪代码。
13)总结
这份SVM的讲义重点概括了SVM的基本概念和基本推导,中规中矩却又让人醍醐灌顶。
从重新审视logistic回归,引出函数间隔(functional margin)和几何间隔(geometric margin);又从间隔问题引出最优间隔分类器(optimal margin classifier);为了解决最优分类器中提到的优化目标函数W的问题,进一步引出拉格朗日对偶(Lagrange duality)和最优间隔分类器问题的拉格朗日对偶形式;推导对偶形式时进一步引出了核(kernel)的概念;最后讨论了不可线性分割情况下的处理以及最终的SMO算法。
拉格朗日对偶的重要作用在于将w的计算提前并消除w,使得优化目标函数W变为拉格朗日乘子的单一参数优化问题(即w至于α有关)。SMO算法的主要目的是求解α。这样,通过拉格朗日对偶和SMO算法,SVM有了良好的理论基础和实现!
SVM的思想确实非常简单,它不再像logistic回归一样企图用整个样本点评价分类效果,而是在样本中去找分隔线,仅通过分隔线附近的样本点评价分类效果。
另外,其他很多议题如SVM背后的学习理论、参数选择问题、二值分类到多值分类等等还没有涉及到,以后有时间再学吧。