POJ1315:Don't Get Rooked
点击打开题目链接
Don't Get Rooked
Description
In chess, the rook is a piece that can move any number of squares vertically or horizontally. In this problem we will consider small chess boards (at most 4x4) that can also contain walls through which rooks cannot move. The goal is to place as many rooks on a board as possible so that no two can capture each other. A configuration of rooks is legal provided that no two rooks are on the same horizontal row or vertical column unless there is at least one wall separating them.
The following image shows five pictures of the same board. The first picture is the empty board, the second and third pictures show legal configurations, and the fourth and fifth pictures show illegal configurations. For this board, the maximum number of rooks in a legal configuration is 5; the second picture shows one way to do it, but there are several other ways. 
Your task is to write a program that, given a description of a board, calculates the maximum number of rooks that can be placed on the board in a legal configuration. Input
The input contains one or more board descriptions, followed by a line containing the number 0 that signals the end of the file. Each board description begins with a line containing a positive integer n that is the size of the board; n will be at most 4. The next n lines each describe one row of the board, with a '.' indicating an open space and an uppercase 'X' indicating a wall. There are no spaces in the input.
Output
For each test case, output one line containing the maximum number of rooks that can be placed on the board in a legal configuration.
Sample Input 4 .X.. .... XX.. .... 2 XX .X 3 .X. X.X .X. 3 ... .XX .XX 4 .... .... .... .... 0 Sample Output 5 1 5 2 4 Source
Mid-Central USA 1998
|
====================================题目大意======================================
在一个有着可以阻碍攻击的墙的棋盘上摆放车，使其相互之间不能攻击，输出能够摆放车的最大数量。
=====================================算法分析=====================================
题目数据水，只要DFS+回溯写对了怎么着都能过。但是这里面有一个不得不说一下的优化。
当判断一个方格中能不能摆放车时，一般的方法是搜索能够攻击到这个方格的其他所有方格中有没有車，但这会造成很多的重复
搜索。
事实上，在摆放车的时候直接将其能够攻击到其它所有方格标记为不可摆放不就行了？
定义一个对应地图的布尔数组HashMap来标记方格。
定义一个函数UpdateHashMap(Row,Col,Val)来将位于方格(Row,Col)中的车能够攻击到的其他所有方格的HashMap值设为Val。
在摆放车的时候调用UpdateHashMap(Row,Col,1)，在回溯的时候调用UpdateHashMap(Row,Col,0)。
就可以直接通过方格对应的HashMap值是否为0来判断其是否可以摆放车了。
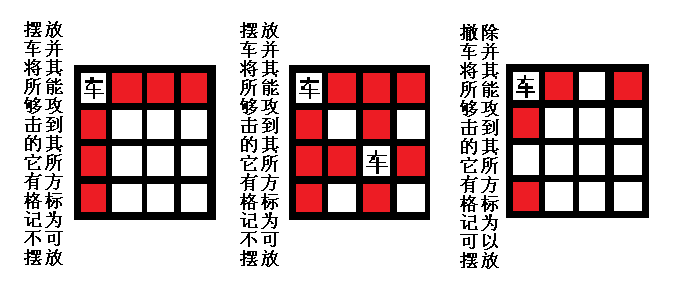
我一开始就是这么做的，结果提交WA了，后来想了想才发现出错的原因，举个出错的例子。
出错的原因很简单，一个车在撤除自己的攻击影响时撤除了其他车的攻击影响。解决方法也很容易想到：
将HashMap改为整形数组，将函数UpdateHashMap(Row,Col,Val)的作用改为将位于方格(Row,Col)中的车能够攻击到的其他所有方格
的HashMap值加Val。
在摆放车的时候调用UpdateHashMap(Row,Col,1)，在回溯的时候调用UpdateHashMap(Row,Col,-1)即可。
=======================================代码=======================================
#include<stdio.h>
const int Dir[4][2]={{0,-1},{0,1},{1,0},{-1,0}};
int N,Ans,HashMap[10][10];
char Map[10][10];
void UpdateHashMap(int Row,int Col,int Val)
{
for(int n=0;n<4;++n)
{
int tmprow=Row;
int tmpcol=Col;
while(1)
{
if(!(0<=tmprow&&tmprow<N)) { break; }
if(!(0<=tmpcol&&tmpcol<N)) { break; }
if(Map[tmprow][tmpcol]!='.') { break; }
HashMap[tmprow][tmpcol]+=Val;
tmprow+=Dir[n][0];
tmpcol+=Dir[n][1];
}
}
}
void DFS(int Row,int Col,int ChessNum)
{
if(Col==N)
{
++Row; Col=0;
}
if(Row==N)
{
Ans=(Ans>ChessNum?Ans:ChessNum); return;
}
if(Map[Row][Col]=='.'&&!HashMap[Row][Col])
{
UpdateHashMap(Row,Col,1);
DFS(Row,Col+1,ChessNum+1);
UpdateHashMap(Row,Col,-1);
}
DFS(Row,Col+1,ChessNum);
}
int main()
{
while(scanf("%d",&N)==1&&N)
{
Ans=0;
for(int i=0;i<N;++i)
{
scanf("%s",Map[i]);
}
DFS(0,0,0);
printf("%d\n",Ans);
}
return 0;
}