迭代式汉诺塔(利用栈实现非递归)

汉诺塔问题的描述：
　　汉诺塔(Tower of Hanoi)问题又称“世界末日问题”有这样一个故事。古代有一个焚塔，塔内有3个基座A,B,C，开始时A基座上有64个盘子，盘子大小不等，大的在下，小的在上。有一个老和尚想把这64个盘子从A座移到B座，但每次只容许移动一个盘子，且在移动过程中，3个基座上的盘子都始终保持大盘在下，小盘在上。移动过程中可以利用C基座做辅助。
　　

　　这个问题当时老和尚和众僧们，经过计算后，预言当所有的盘子都从基柱A移到基座B上时，世界就将在一声霹雳中消灭，而梵塔、庙宇和众生也都将同归于尽。其实，不管这个传说的可信度有多大，如果考虑把64个盘子，由一个塔柱上移到另一根塔柱上，并且始终保持上小下大的顺序。假设有n个盘子，移动次数是f(n).显然f(1)=1,f(2)=3,f(3)=7,且f(k+1)=2*f(k)+1。此后不难证明f(n)=2n-1。n=64时， f(64)= 2^64-1=18446744073709551615     假如每秒钟一次，共需多长时间呢？一年大约有 31536926 秒，计算表明移完这些金片需要5800多亿年，比地球寿命还要长，事实上，世界、梵塔、庙宇和众生都早已经灰飞烟灭。 

       假设有三个盘子时：

利用递归的方法可以推出如下算法：
第一步 把A上的n-1个圆盘移到C上； 
第二步 把A上的一个圆盘移到B上； 
第三步 把C上的n-1个圆盘移到B上；

         递归其实是用栈存储当前的运行时执行状态来执行递归函数，在它每次从递归调用返回时，都会弹出运行时栈顶的顶部状态，使得它可以继续做余下的事情。下面就是根据系统递归调用的执行方式自己使用显示栈来消除递归。

以下为实现代码（直接使用标准c++中的stack容器）：

#include <iostream>
#include <stack>

struct Quad {
	Quad();
	Quad(int n, char a, char b, char c): _n(n), _x(a), _y(b), _z(c) {
	}
	int _n; 		// 要移动的盘子数量
	char _x, _y, _z; 	// 保存柱子名称
}; // 保存当前状态

void hanoi(int, char, char, char);

int main(int argc, char *argv[])
{
	hanoi(3, 'A', 'B', 'C');

	return 0;
}

void hanoi(int n, char x, char y, char z)
{
	std::stack<Quad> s;
	s.push(Quad(n, x, y, z));
	while (!s.empty()) {
		Quad q = s.top();
		s.pop();
		n = q._n;
		x = q._x;
		y = q._y;
		z = q._z;
		if (n == 1) {
			std::cout << "Move top disk from peg " << q._x
				 << " to peg " << q._z << "\n";
		}
		else {
			s.push(Quad(n - 1, y, x, z));
			s.push(Quad(1, x, y, z));
			s.push(Quad(n - 1, x, z, y));
		}
	}
}

         其中Quad结构用于保存4个元素，包括一个整数和三个字符，通过把一个保存当前状态的Quad对象压入到栈上来替换每个递归调用，直到栈空为止。

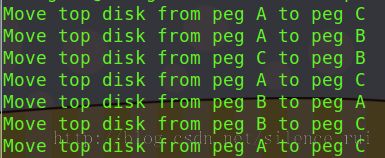
运行结果：