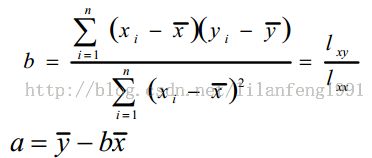R语言之回归分析篇
转载自:http://blog.csdn.net/lilanfeng1991/article/details/18841177
回归分析:
相关分析:是否相关,相关方向,相关程度
7.1 一元线性回归
7.1.1 拟合模型
回归分析是将相关的因素进行测定,确定其因果关系,并以数学模型来表现其具体关系式,从而进行的各类统计分析。
其主要步骤有:建立回归模型、求解回归模型中的参数、对回归模型进行检验等
最小二程法:
例:
用R做线性回归:一个人的最大心率和年龄的关系是由方程MaxRate=220-Age来决定的。假设这是符合经验数据的,有15个来自不同年龄层的人接受了最大心率测试,数据如下:
Age(x)18 23 25 35 65 54 34 56 72 19 23 42 18 39 37
MaxRate(y)202 186 187 180 156 169 174 172 153 199 193 174 198 183 178
> x=c(18,23,25,35,65,54,34,56,72,19,23,42,18,39,37)
> y=c(202,186,187,180,156,169,174,172,153,199,193,174,198,183,178)
> plot(x,y) #绘制散点图
> fm=lm(y~x) #拟合线性回归模型
> abline(fm) #绘制回归线
> fm
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x
210.0485 -0.7977
7.1.2 检验假定
模型的有效性可使用命令EDA以图形化的方式进行检验。
可用EDA画图来检验数据的正态性
通过观察数据当中是否存在趋势可检验相关性,可通过画残差对时间的图形来解决。
通过画残差对时间和拟合值的图形来检验误差项是否具有同方差。
1 预测残差图(Residuals vs .fitted):画预测值和残差值的图形,检查直线y=0四周的点,看是否无明显的趋势;
2 QQ正态检验(QQplot):若所有的点近似直线,则残差就是正态分布;
3 尺度-位置诊断图(Scale):给出标准化残差的平方根,高的点对应较大的残差。
4 Cook距离(Cook's distance):给出对回归线影响圈套的点。
7.1.3 模型检验
7.1.4 置信区间
7.2 多元线性回归
简单线性回归:一个自变量对因变量的影响程度
多元线性回归:有多个自变量或回归元
7.2.1 模型简介
7.2.2 模型拟合
例:
> x1=1:20
> x2=sample(1:100,20)
> y=x1+x2
> lm(y~x1+x2)
Call:
lm(formula = y ~ x1 + x2)
Coefficients:
(Intercept) x1 x2
-3.654e-14 1.000e+00 1.000e+00
> y=x1+x2+rnorm(20,0,2)
> lm(y~x1+x2)
Call:
lm(formula = y ~ x1 + x2)
Coefficients:
(Intercept) x1 x2
0.05669 0.93572 0.99859
> y=x1+x2+rnorm(20,0,10)
> lm(y~x1+x2)
Call:
lm(formula = y ~ x1 + x2)
Coefficients:
(Intercept) x1 x2
2.2214 0.7479 0.9715
可知:噪声越多,置信估计就越差;样本量越大,置信估计就越好;
7.2.3 实证分析
例:
本例收集1990-2001共12年财政收入相关数据,分析财政收入(y,百亿元)和国民生产总值(x1,百亿元)、税收(x2,百亿元)、进出口贸易总额(x3,百亿元)、 经济活动人口(x4,百万人)之间的关系。
解:
> reg=read.table("C:\\Users\\lenovo\\Desktop\\reg.txt")
> reg
y x1 x2 x3 x4
1990 29.3710 185.984 28.2187 55.601 653.23
1991 31.4948 216.625 29.9017 72.258 660.91
1992 34.8337 266.519 32.9691 91.196 667.82
1993 43.4895 345.605 42.5530 112.710 674.68
1994 52.1810 466.700 51.2688 203.819 681.35
1995 62.4220 574.949 60.3804 234.999 688.55
1996 74.0799 668.505 69.0982 241.338 697.65
1997 86.5114 731.427 82.3404 269.672 708.00
1998 98.7595 769.672 92.6280 268.577 720.87
1999 114.4408 805.794 106.8258 298.963 727.91
2000 133.9523 882.281 125.8151 392.742 739.92
2001 163.8604 943.464 153.0138 421.933 744.32
> pairs(reg)
> pairs(reg)#矩阵散点图
> fm=lm(y~x1+x2+x3+x4) #拟合多元线性模型
> fm=lm(y~x1+x2+x3+x4)
> fm
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x
210.0485 -0.7977
> anova(fm)#模型假设检验-方差分析
Analysis of Variance Table
Response: y
Df Sum Sq Mean Sq F value Pr(>F)
x 1 2724.50 2724.50 130.01 3.848e-08 ***
Residuals 13 272.43 20.96
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> summary(fm)$coef #回归系数的假设检验-t检验
Estimate Std. Error t value Pr(>|t|)
(Intercept) 210.0484584 2.86693893 73.26576 2.124074e-18
x -0.7977266 0.06996281 -11.40215 3.847987e-08
> plot(rownames(reg),reg$y,type="p",xlab="year")
> lines(rownames(reg),fm$fit)#模型拟合效果比较