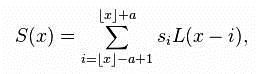Image Scaling
在图像处理技术中,图像缩放是一个比较常见和简单的算法。虽然说简单,但是如果要做到效果好而且速度快还是有一定难度的。最近有涉及到图像缩放的东西,对一些常用的算法进行一些简单的介绍和总结。
在移动上平台上,一般拍照的分辨率都非常大,要对拍照后的图像进行处理则非常耗时,一般需要进行下采样。如果下采样质量较差则会影响后处理的效果,所以要采用一种效率高和质量好的插值算法。
- 最近邻插值
最简单的一种算法,其思想是通过缩放系数得到坐标之间的对应关系,直接取整得到原始图像中的坐标,然后获取其像素值就是缩放后图像的像素值。如下图P和D点最近,则取D点的像素值。
- 双线性插值
对于目标像素,通过缩放比例得到原始图像的浮点型坐标(i+u,j+v),然后取其周围四个点进行如下计算:f(i,j)为其像素值
f(i+u,j+v) = (1-u)*(1-v)*f(i,j) + (1-u)*v*f(i,j+1)+ u*(1-v)*f(i+1,j) + u*v*f(i+1,j+1)
如下图所示:
- 双立方插值
这个算法如下图所示,利用P点的周围16点的值进行非线性计算,在维基百科上有算法的具体介绍:http://en.wikipedia.org/wiki/Bicubic_interpolation。
f(i+u,j+v) = [A] * [B] * [C]
[A] = [ S(u + 1) S(u + 0) S(u - 1) S(u - 2) ]
┏ f(i-1, j-1) f(i-1, j+0) f(i-1, j+1) f(i-1, j+2) ┓
[B]=┃ f(i+0, j-1) f(i+0, j+0) f(i+0, j+1) f(i+0, j+2) ┃
┃ f(i+1, j-1) f(i+1, j+0) f(i+1, j+1) f(i+1, j+2) ┃
┗ f(i+2, j-1) f(i+2, j+0) f(i+2, j+1) f(i+2, j+2) ┛
┏ S(v + 1) ┓
[C]=┃ S(v + 0) ┃
┃ S(v - 1) ┃
┗ S(v - 2) ┛
┏ 1-2*Abs(x)^2+Abs(x)^3 , 0<=Abs(x)<1
S(x)=┃ 4-8*Abs(x)+5*Abs(x)^2-Abs(x)^3 , 1<=Abs(x)<2
┗ 0 , Abs(x)>=2
S(x)是对 Sin(x*Pi)/x 的逼近:
- 卷积插值
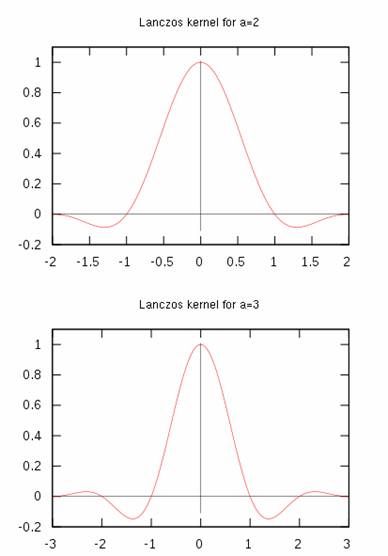
这里介绍一下Lanczos插值方法,Lanczos Kernel是一个sinc函数,效果被认为是效率和效果最折中的插值方法。
Lanczos Kernel表达式:
插值公式:
Lanczos Kernel是一个连续的函数,其导数在任何地方也是连续的,所以对于重建信号S(x)来说也是一个连续的信号。这种方法在突变的采样像素区域如强边缘处会产生振铃效应,但在一定程度上也会有增强边缘的作用。有论文提到过这种插值方法是Best compromise in termsof reduction of aliasing, sharpness, and minimal ringing.可以参考论文Filters for CommonResampling Tasks。
如降采样4.5倍的时候的插值系数为:
{-1, -2, -2,2, 10, 18, 25, 28,25, 18, 10, 2, -2, -2, -1 },
{ 0, -2, -2,0, 6, 14, 22, 27,27, 22, 14, 6, 0, -2, -2 },
有两组系数,原图中9个点采样出2个点,第一个点用第一组系数,第二个点用第二个系数。在C语言实现中可以采用先行后列的加速办法实现。可以采用NEON指令进行优化,结果证明优化后提高了10倍左右。1080p的图像几十ms内完成,达到了实用的要求。有时间的话我会介绍一下如何进行优化。
百科上也介绍了一些Scaling的方法包括Spline Interpolation、SuperSamping等。
http://en.wikipedia.org/wiki/Image_scaling#Pixel_art_scaling_algorithms