由rand7生成rand10以及随机数生成方法的讨论
ZZ 毕达哥拉斯半圆
问题:rand7是一个能生成1-7的整数随机数。要求利用rand7生成1-10的整数随机数。可以 参看原帖。在lz提示下又找到了更简洁的方法,同余循环法,只需要一行代码!我很浅的探讨几种方法,还需要更深入的学习。感慨一下知识的浩瀚和自己的渺小。
1.组合数学方法
我在帖子里给出了这样的方法,这个很简单的算法,却似乎不那么容易被理解。
第1次 1 2 3 4 5 6 7 之中用rand7取一个数
第2次从 2 3 4 5 6 7 8 之中取一个数
第3次从 3 4 5 6 7 8 9 之中取一个数
第4次从 4 5 6 7 8 9 10 之中取一个数
第5次从 5 6 7 8 9 10 1 之中取一个数
第6次从 6 7 8 9 10 1 2 之中取一个数
...
第10次从 10 1 2 3 4 5 6 之中用取一个数
1-10每个数字在上表中都出现了7次,共有70个数字,这样每个数字被命中的概率为1/10。
这里的关键词是"命中".
第11次重新循环,从 1 2 3 4 5 6 7 之中取一个数
第12次从 2 3 4 5 6 7 8 之中取一个数
......
按照这样的方法,1-10每个数字被命中的概率是均匀分布。而1-10次的数组,本质上是生成了所有1-10按照次序的一个轮换结构,也就是组合问题中的生成所有排列。(参见Knuth 第4卷第2册(The Art Of Computer Programming, Volume4, Generating All Tuples and Permutations))在经过比较长的时间之后,就可以观察到均匀分布。事实上,任何随机数算法都需要经过比较长的过程才能观察出他的分布,而概率分布,是在一个统计意义上的概念。
由此还可以得出 用m个随机数生成n个随机数的方法。
1. 当m > n的时候,用舍去法,每次n个随机数,超过这个范围就舍弃,再来一次。
2. 当m < n的时候,用如上的方法建立m大小的数组,其中的数字在1到n按照次序循环轮换,这样n*m个循环之后,就可以得到均匀的n个随机数。
2. 同余循环法
3. 舍去法
这个题在考试中大概是不让用舍去法的,因为他太平凡。但实际上舍入法也很有用,因此还是写出来,后面还会再提到舍入法。
1. 第一次用rand7取出1到5的随机数,记为a
2. 第二次用rand7取出1或2,记为b
3. 如果b = 1, 则c = a, 如果b = 2,则c = a + b
4. 返回c
4. 利用对rand7的组合计算
有很多网友包括我自己也曾经用(rand7()+rand7()+7+rand7()+14+....)%10的方法类生成随机数,还有希望用rand7()*rand7()*rand7().....然后再做各种计算来生成。随后我意识到这样只能得到 近似的均匀。
从统计学的角度上看,n个rand7的计算结果是就是具有独立同分布(iid)的n个随机变量的联合分布,也就是若X1,X2,...Xn~U(1,7)(服从1-7的均匀分布),而计算之后的结果符合f(x1,x2,...xn)的联合概率分布,现在将多元的f(x1,x2,...xn)分布变换到U(1,10),如果不用筛选法,难度是非常大的。而 在本例是不可能的,这是因为:
1)对rand7的一元运算只能有7种结果,不可能产生10个随机数
2)现在有二元运算(X)可以是加减乘除或者任何函数任何映射关系,rand7(X)rand7的可能运算方式是7*7种,,n次二元(X)运算后的可能是运算方式是7^(n+1)种,现在要用7^(n+1)种运算过程得到均匀的10种结果,这是不可能的,(因为7^n不能被10整除),所以只能是近似均匀。
还有人希望用这样的方法:调用两次rand7从而生成一个7进制的数,然后转换成0-49,刚好是50个数的均匀分布,再取模10。这个方法貌似可行,可是很遗憾的是,这样生成的7进制0-66对应到10进制是0-48,而不是49,少了一个数。
5. 连续随机变量的分布
本题的rand7是一个离散随机变量,只取1-7的整数。离散变量的缺点是在数学计算上不方便,因此可以转成连续随机变量。也就是从rand7生成1-7的连续均匀分布,获得1-10的均匀分布。虽然本题不适用这个方法,但是本题除了考试有用,在实际应用中不会出现,更多的方法是从一种分布变换到另外一种分布。
现在的答案很简单,从几何的角度上看,我们可以把[a,b]线段上的点按照一对一映射到另一个线段[c,d]上去,只需要做一个线性变换y=(x-a)/(b-a)*(d-c)+c. 那么,若rand()~U(a,b),则y=(rand()-a)/(b-a)*(d-c)+c~U(c,d),也就是如果rand()是a到b上的均匀分布,则y=(d-c)(x-a)/(b-a)+c是c到d上的均匀分布。对于本例rand10=(rand()-1)/6*9+1. 下面是证明,更一般的情况同理可证:
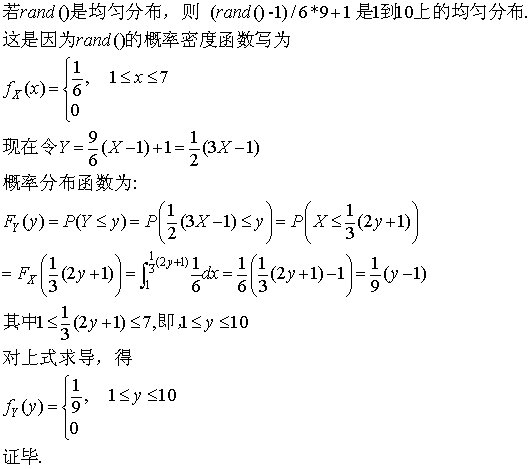
另外有一个重要的定理来表明变换之后的分布。这可以处理如Y=X^2, Y=e^X等多种变换。定理如下:
这个定理还可以更强一些,f(x)是分段还是也可以,甚至只是一个覆盖(包括)就可以了。从符合一种分布的随机数生成另外一种分布的随机数是统计模拟的课题,其中有非常有趣的变换方法,例如,如果X是(0,1)上的均匀分布,则Y=-a*log(X)是指数分布。这些内容,参考《 统计推断》,或者更进一步的材料。
6. 再谈舍入法
C语言的rand函数,可能是用了线性同余算法获得均匀分布,这类叫直接方法。我118楼还提到了利用变换从均匀分布获得其他分布的方法,这些都叫直接法。舍去法也是非常重要的一类随机,用来生成各种分布的随机数,比如Metropolis算法,比较著名的还有Markov Chain Monte Carlo (MCMC)算法,这类方法可以看成是一个黑盒子,要求在算法内部通过几次运算很快收敛到一种概率分布,然后返回一个随机数。参见Casella & Berger 统计推断(Statistical Inference)以及 Kunth第2卷Seminumerical Algorithms, Random Numbers.
1.组合数学方法
我在帖子里给出了这样的方法,这个很简单的算法,却似乎不那么容易被理解。
第1次 1 2 3 4 5 6 7 之中用rand7取一个数
第2次从 2 3 4 5 6 7 8 之中取一个数
第3次从 3 4 5 6 7 8 9 之中取一个数
第4次从 4 5 6 7 8 9 10 之中取一个数
第5次从 5 6 7 8 9 10 1 之中取一个数
第6次从 6 7 8 9 10 1 2 之中取一个数
...
第10次从 10 1 2 3 4 5 6 之中用取一个数
1-10每个数字在上表中都出现了7次,共有70个数字,这样每个数字被命中的概率为1/10。
这里的关键词是"命中".
第11次重新循环,从 1 2 3 4 5 6 7 之中取一个数
第12次从 2 3 4 5 6 7 8 之中取一个数
......
按照这样的方法,1-10每个数字被命中的概率是均匀分布。而1-10次的数组,本质上是生成了所有1-10按照次序的一个轮换结构,也就是组合问题中的生成所有排列。(参见Knuth 第4卷第2册(The Art Of Computer Programming, Volume4, Generating All Tuples and Permutations))在经过比较长的时间之后,就可以观察到均匀分布。事实上,任何随机数算法都需要经过比较长的过程才能观察出他的分布,而概率分布,是在一个统计意义上的概念。
由此还可以得出 用m个随机数生成n个随机数的方法。
1. 当m > n的时候,用舍去法,每次n个随机数,超过这个范围就舍弃,再来一次。
2. 当m < n的时候,用如上的方法建立m大小的数组,其中的数字在1到n按照次序循环轮换,这样n*m个循环之后,就可以得到均匀的n个随机数。
2. 同余循环法
mingliang1212提示我上面这个方法,实际上等价于(rand7() + i)%10,i从0-9反复循环,而每次计算的余数恰好与上面的方法等价。也就是用利用同余的性质生成所有排列,这真是一个巧妙的想法!于是:
于是上面 用m个随机数生成n个随机数的方法的,也有了更简洁的算法,步骤与此类似就不写了。感慨一下数学的力量!也谢谢 mingliang1212
1. i从0到9反复循环
2. (rand7()+i)%10,产生0-9的随机数,等效与第一种组合法(只需要把上面表中的1-10改成0-9)
3. 再+1得到1-10的随机数
优化后只需要一行代码!本文最后给出了这个代码。
2. (rand7()+i)%10,产生0-9的随机数,等效与第一种组合法(只需要把上面表中的1-10改成0-9)
3. 再+1得到1-10的随机数
于是上面 用m个随机数生成n个随机数的方法的,也有了更简洁的算法,步骤与此类似就不写了。感慨一下数学的力量!也谢谢 mingliang1212
3. 舍去法
这个题在考试中大概是不让用舍去法的,因为他太平凡。但实际上舍入法也很有用,因此还是写出来,后面还会再提到舍入法。
1. 第一次用rand7取出1到5的随机数,记为a
2. 第二次用rand7取出1或2,记为b
3. 如果b = 1, 则c = a, 如果b = 2,则c = a + b
4. 返回c
4. 利用对rand7的组合计算
有很多网友包括我自己也曾经用(rand7()+rand7()+7+rand7()+14+....)%10的方法类生成随机数,还有希望用rand7()*rand7()*rand7().....然后再做各种计算来生成。随后我意识到这样只能得到 近似的均匀。
从统计学的角度上看,n个rand7的计算结果是就是具有独立同分布(iid)的n个随机变量的联合分布,也就是若X1,X2,...Xn~U(1,7)(服从1-7的均匀分布),而计算之后的结果符合f(x1,x2,...xn)的联合概率分布,现在将多元的f(x1,x2,...xn)分布变换到U(1,10),如果不用筛选法,难度是非常大的。而 在本例是不可能的,这是因为:
1)对rand7的一元运算只能有7种结果,不可能产生10个随机数
2)现在有二元运算(X)可以是加减乘除或者任何函数任何映射关系,rand7(X)rand7的可能运算方式是7*7种,,n次二元(X)运算后的可能是运算方式是7^(n+1)种,现在要用7^(n+1)种运算过程得到均匀的10种结果,这是不可能的,(因为7^n不能被10整除),所以只能是近似均匀。
还有人希望用这样的方法:调用两次rand7从而生成一个7进制的数,然后转换成0-49,刚好是50个数的均匀分布,再取模10。这个方法貌似可行,可是很遗憾的是,这样生成的7进制0-66对应到10进制是0-48,而不是49,少了一个数。
5. 连续随机变量的分布
本题的rand7是一个离散随机变量,只取1-7的整数。离散变量的缺点是在数学计算上不方便,因此可以转成连续随机变量。也就是从rand7生成1-7的连续均匀分布,获得1-10的均匀分布。虽然本题不适用这个方法,但是本题除了考试有用,在实际应用中不会出现,更多的方法是从一种分布变换到另外一种分布。
现在的答案很简单,从几何的角度上看,我们可以把[a,b]线段上的点按照一对一映射到另一个线段[c,d]上去,只需要做一个线性变换y=(x-a)/(b-a)*(d-c)+c. 那么,若rand()~U(a,b),则y=(rand()-a)/(b-a)*(d-c)+c~U(c,d),也就是如果rand()是a到b上的均匀分布,则y=(d-c)(x-a)/(b-a)+c是c到d上的均匀分布。对于本例rand10=(rand()-1)/6*9+1. 下面是证明,更一般的情况同理可证:
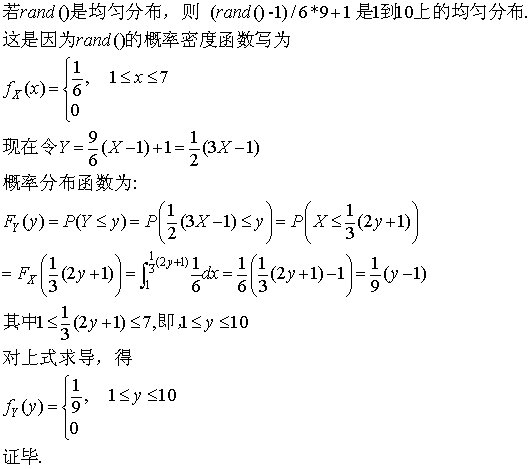
另外有一个重要的定理来表明变换之后的分布。这可以处理如Y=X^2, Y=e^X等多种变换。定理如下:
这个定理还可以更强一些,f(x)是分段还是也可以,甚至只是一个覆盖(包括)就可以了。从符合一种分布的随机数生成另外一种分布的随机数是统计模拟的课题,其中有非常有趣的变换方法,例如,如果X是(0,1)上的均匀分布,则Y=-a*log(X)是指数分布。这些内容,参考《 统计推断》,或者更进一步的材料。
6. 再谈舍入法
C语言的rand函数,可能是用了线性同余算法获得均匀分布,这类叫直接方法。我118楼还提到了利用变换从均匀分布获得其他分布的方法,这些都叫直接法。舍去法也是非常重要的一类随机,用来生成各种分布的随机数,比如Metropolis算法,比较著名的还有Markov Chain Monte Carlo (MCMC)算法,这类方法可以看成是一个黑盒子,要求在算法内部通过几次运算很快收敛到一种概率分布,然后返回一个随机数。参见Casella & Berger 统计推断(Statistical Inference)以及 Kunth第2卷Seminumerical Algorithms, Random Numbers.
7. 本题的代码
//1. 组合数学法的实现
#include <stdio.h>
#include <stdlib.h>
#include <memory.h>
#include <time.h>
static int x[7] = {1, 2, 3, 4, 5, 6, 7}; //轮转数组,初始为1-7
//每调用1次,实现一次1-10的轮转
void shift_array()
{
memcpy(x, x + 1, 6 * sizeof(int));
x[6] = (*x + 6) % 10;
if (!(x[6])) x[6] = 10; //这里可能有更好的写法
}
//返回1-10的随机数,不要忘记先调用srand()
int rand10()
{
shift_array(); //轮转一次
return x[rand() % 7]; //随机返回数组内的一个数字
}
void main(void)
{
unsigned int result[10] = {0};
int k; srand((unsigned int)time(0)); //设定种子
for (k = 0; k < 100000; k++)
result[rand10() - 1]++;
for (k = 0; k < 10; k++)
printf("%d : %.05f\n", k + 1, (double)result[k]gloabl_i/100000);
}
//2. 同余循环法,本方法与上面的区别只在于实现循环方式的不同
static unsigned int gi = 0;
//a = rand() % 7 + 1 :生成1-7的随机数
//b = i++ % 10 : i从0-9循环
//(a + b) % 10,循环产生0-9的随机数,详见第一种方法的论述
//这个结果再+1,生成1-10随机数
//再提醒不要忘记先调用srand()
int new_rand10()
{
return (((rand() % 7 + 1) + (gi++ % 10)) % 10) + 1;
}