Dijkstra 最短路径算法 图示与实现

基本思想：

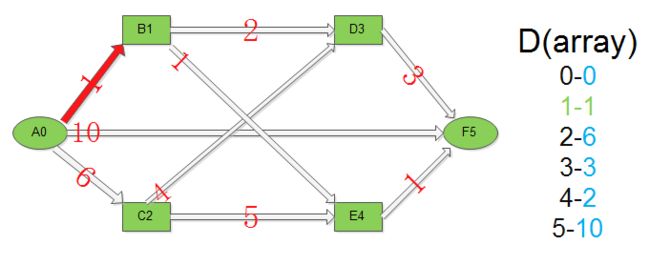
每次从当前的最短路径中选出一个，并利用该节点优化图中起始点至图中其它各未访问到的节点的距离。以下图为例，我们欲求出起始点(A)至其它各节点的最短路径：

用数组D来存储A至其它各节点当前路短的距离，例如：D[1]为A-B的当前最短距离，D[2]为A-C当前最短距离。

起始状态为D[0]=0,根据图的连通关系，可以得到：

D[1] = D[0]+L(0->1) = 1

D[2] = D[0]+L(0->2) = 6

D[5] = D[0]+L(0->5) = 10

把D[0]标记为已处理

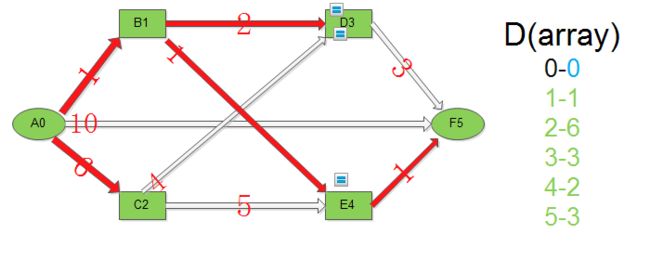
从未处理过的节点中找出d值最小的节点，由于D[1]=1且B1未被处理过，所以B1为这一步的候选节点，接下来可能得到优化后的D数组：

D[3] = 3

D[4] = 2

将D[1]标记为已处理

同理可以找到最优候选节点E4,优化D数组：

D[5] = Min(D[5], D[4]+1) = 3

选取D3节点：

选取E5节点：

选取C2节点：

处理完成，得到A0到其它任意节点的最短距离

/*
 * dijkstra.cc
 *
 *  Created on: Jan 5, 2013
 *      Author: guixl
 */


#include <stdio.h>
#include <string.h>

const int MAX_VERTEX = 100;
const int INF = 1<<30;
int graph[MAX_VERTEX][MAX_VERTEX];

int d[MAX_VERTEX];
int prefix[MAX_VERTEX];
int visit[MAX_VERTEX];
int vertex_number=6;

void BuildGraph() {
	memset(graph, -1, sizeof(graph));
	graph[0][1] = 1;
	graph[0][2] = 6;
	graph[0][5] = 10;
	graph[1][3] = 2;
	graph[1][4] = 1;
	graph[2][3] = 4;
	graph[2][4] = 5;
	graph[3][5] = 3;
	graph[4][5] = 1;
}

void dijkstra() {
	for (int i=0; i<vertex_number; i++)
		d[i] = i==0 ? 0 : INF;
	memset(visit, 0, sizeof(visit));

	for (int i=0; i<vertex_number; i++) {
		int min_v, min_value=INF;
		for (int j=0; j<vertex_number; j++) {
			if (d[j]<min_value && !visit[j])
				min_value = d[min_v=j];
		}
		visit[min_v] = 1;
		for (int j=0; j<vertex_number; j++)
			if (graph[min_v][j] >= 0) {
			if(d[min_v]+graph[min_v][j] < d[j]) {
				d[j] = d[min_v]+graph[min_v][j];
				prefix[j] = min_v;
			}
		}
	}
}

void Print() {
	for (int i=0; i<vertex_number; i++) {
		printf("Shortest path from 0 to %d is %d:\n", i, d[i]);
		for (int s=i; s!=0; s=prefix[s]) {
			printf("%d->%d\n", prefix[s], s);
		}
	}
}

int main(int argc, char** argv) {
	BuildGraph();
	dijkstra();
	Print();
	return 0;
}

运行结果：

guixl@guixl-ThinkPad-T61:~/workspace/blog_source_code/src$ ./test 
Shortest path from 0 to 0 is 0:
Shortest path from 0 to 1 is 1:
0->1
Shortest path from 0 to 2 is 6:
0->2
Shortest path from 0 to 3 is 3:
1->3
0->1
Shortest path from 0 to 4 is 2:
1->4
0->1
Shortest path from 0 to 5 is 3:
4->5
1->4
0->1