斯坦福机器学习公开课笔记(五)--神经网络的表示
公开课地址:https://class.coursera.org/ml-003/class/index
授课老师:Andrew Ng
1、non-linear hypotheses(非线性假设)
前面提到的都是回归方面的东西,现在要开始新的一个专题-神经网络。自然,脑中冒出一个问题,为什么要引入神经网络?
还是考虑房屋售价预测问题,我们可以通过引入多个特征让预测更准确,但我们知道能引入的特征数目不多。如果特征数目变多,例如从100*100个pixels中选出所有XiXj作为逻辑回归的一个参数,那么总共就有5*10^7个特征。如果采用之前的线性假设,那处理这么多特征代价将会很大。为此我们引入了非线性假设来应对高维数据。非线性是指两个变量间的关系,是不成简单比例(即线性)关系的。
上图为一个区分是否为汽车的模型,我们可以看到如果用线性假设,选取图中的像素点,那么X表示成一个2500维向量,XiXj就是300万的特征,代价太大。如果采用非线性假设,如左图所示,那么两个像素点就能构造出一个模型来对是不是汽车进行判断。
2、neurons and brain(神经元和大脑)
为了引入神经网络,首先要介绍一下人的大脑。关于人脑,我们都知道其中有专门负责视觉、听觉、味觉等等的区域,如下面这些图所示:
对人脑有个基本认识足够了,脑科学太高深了。
3、model representation one(模型表示1)
还是人脑,不过现在关注的是人脑中的神经元:
从上图可以看到神经元有树突,轴突等等组成,不过我们只需要知道神经元接受外界刺激信号,然后产生一个输出即可。抽象表示如下:
上图中有三个输入,一个输出,中间黄色的圈代表神经元。考虑到每一个神经元都有一个阈值,超过这个阈值才会产生输出,我们为了简化把这个限制条件以增加一个额外输入的形式体现出来,X0为新增加的输入,其值恒为1,theta0为那条边上的权重,两个值相乘就是阈值。对于多层的情况,我们在输入和中间层增加一个额外输入即可:
现在搞清楚了神经网络的基本结构,下面就是如何计算的问题了:
上图中没有标出额外的输入,但是计算过程中用到了。计算过程就是输入乘以对应的权重,a是激活值,这里代表某个节点的输出。这里需要注意theta的维度,额外输入导致增加一列。
4、model representation two(模型表示2)
我们可以把上面的计算过程以向量化的形式进行表达:
右侧就是向量化的表达形式,这样写比较简化。对于层数更多的神经网络,计算方法是类似的:
5、examples and intuitions one(直观例子1)
这里用神经网络实现一个简单的例子,与的操作:
从上图可以看到,输入是x1,x2,输入边的权值都是20, -30是阈值,输出是对三个值求和再求sigmoid函数,通过输入真值表中的不同取值,我们能看到计算得到的值与我们通过逻辑运算得到的值接近,可以认为这个神经网络就实现了两个输入的与的运算。下面的或运算也是类似的:
6、examples and intuitions one(直观例子2)
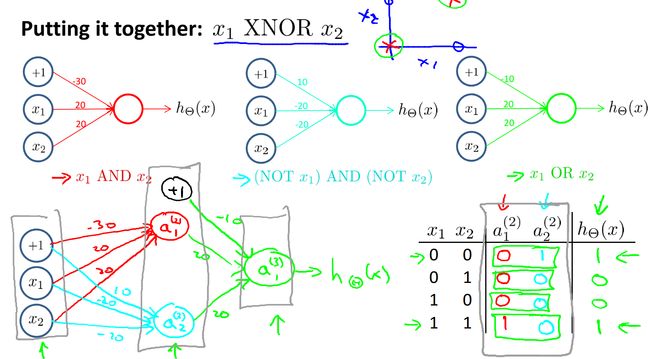
下面考虑一个更复杂的例子,X1 XNOR X2,翻译是同或门。首先我们需要知道:
X1 XNOR X2=(X1 AND X2)OR((NOT X1) AND (NOT X2)),接下来可以首先求出每一个部分的神经网络,最后拼接起来即可。首先是非NOT的:
然后是其他部分:
可以直观发现左下方实现XNOR的神经网络是上面三个神经网络的叠加。
7、multi-class classification(多分类问题)
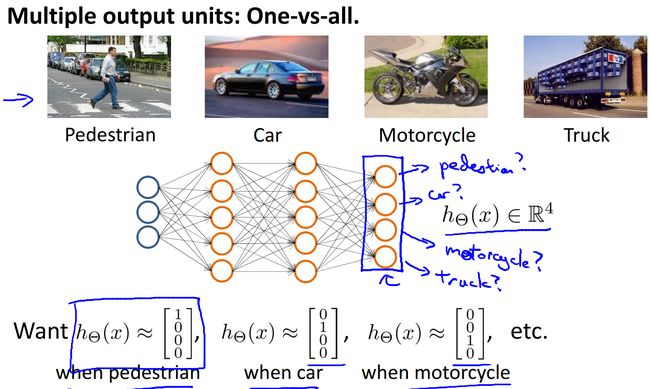
之前在逻辑回归中提到过求解多分类问题需要构造多个函数,每次只能分出一类。现在有了神经网络,我们只需要依据类别数目设置多个输出单元,然后判断对应的输出单元是否为1即可,由于每次输出时只有一个单元为1,这样就能标记出类别信息。
上图就是四个输出单元,第一个输出为1表明是行人,第二个输出为1表明是汽车,依次类推。
-------------------------------------------------弱弱的分割线--------------------------------------------------
这一讲主要是引入了神经网络的概念,让我们见识到非线性问题完全可以用其来解决。相比线性回归,逻辑回归,神经网络更加直观也更为简单一些,只需要设定好神经网络的结构和参数,提供输入就能得到输出。当然,这些只是神经网络最简单的知识,它还有其他更重要的方面有待学习。