MATLAB旋转体的绘制
MATLAB旋转体的绘制
使用mesh绘制旋转体
原理:绘制旋转体,在于确定旋转的曲线以及所要绕着旋转的轴。例如,将一个YoZ平面上的半圆:z^2+(y-r)^2 = 1(z>=0)绕z轴旋转而成的旋转体。示意图如下:
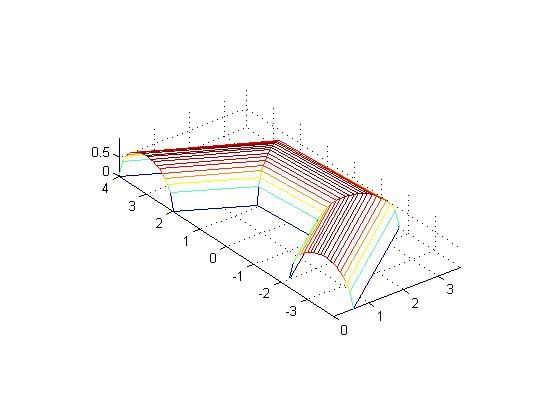
当绕z轴旋转alpha角度时(实际是逆时针旋转,这里为方便观察画成顺时针),z坐标不变,y坐标变为y*cos(alpha),x坐标为y*sin(alpha),使用mesh绘图时,需要提供所有点的坐标,使用矩阵形式。如果是alpha为0,则是对应的一个半圆的坐标,为1,又是一个。所以使用列向量乘以行向量,得到若干半圆的坐标。先画4个半圆观察一下:
r = 2;
y = linspace(r,r+2,20);
z = sqrt(1-(y-1-r).^2);
alpha = 0:1:3;
X = y'*sin(alpha)
Y = y'*cos(alpha)
Z = z'*ones(1,4)
mesh(X,Y,Z)
axis equal vis3d
XYZ之所以不加分号是可以观察一下形成的3个矩阵。其中每一列对应一个半圆的3个坐标。这是效果图:
注意其实旋转方向是正确的,只是MATLAB的y坐标的方向是反着的。
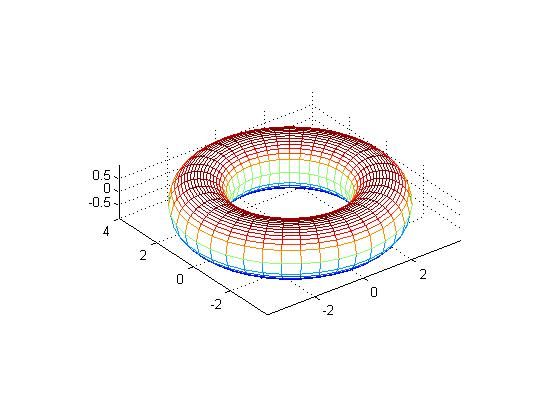
如此,可以改变alpha的取值,便可以得到比较光滑的旋转体了。以下是程序和效果图:
r = 2;
y = linspace(r,r+2,20);
z = sqrt(1-(y-1-r).^2);
alpha = linspace(0,2*pi,40);
X = y'*sin(alpha)
Y = y'*cos(alpha)
Z = z'*ones(1,40)
mesh(X,Y,Z)
hold on
mesh(X,Y,-Z)
axis equal vis3d
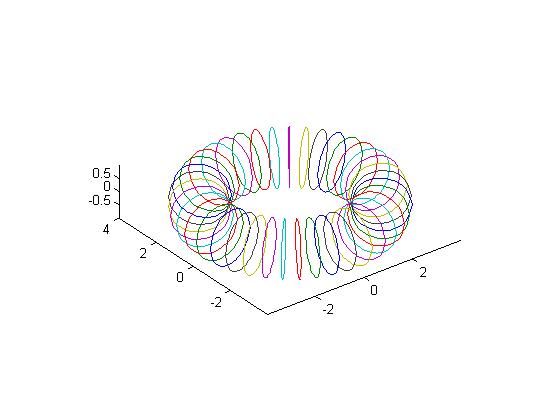
当然亦可以使用plot3,这是plot3的效果图:
mesh与plot3的原理
一下是mesh帮助文档的节选翻译:
mesh(X,Y,Z)画一个线框曲面,曲面的颜色由Z坐标决定,因此颜色是由曲面高度按比例绘制的。如果X和Y是向量,X的长度为n,Y的长度为m,则[m,n] = size(Z)。这时,(X(j),Y(i),Z(i,j))是线框的横截面。补充说明,这是我说的哈:其实可以想象一下从Z轴看下去的俯视图,其形状如下:
| x1 |
x2 |
... |
xn |
|
| y1 |
z11 |
z12 |
... |
z1n |
| y2 |
z21 |
z22 |
... |
z2n |
| ... |
... |
... |
... |
... |
| ym |
zm1 |
zm2 |
... |
zmn |
接着翻译:X和Y的大小必须和Z符合。如果X和Y是矩阵,(X(i,j),Y(i,j),Z(i,j))就是线框的横截面了。
额,都是i和j了,可以先固定一个,例如i=1,j从1取到n,是一条线,再固定j,i从1取到m,又是一条线,如此将所有的线条画出,就ok了。一下实验可以体现其工作特点,可以通过矩阵来对照图形观察一下:
X = [1 -1 -1 1 1;1 -1 -1 1 1;1 -1 -1 1 1;1 -1 -1 1 1;1 -1 -1 1 1]
Y = [1 1 -1 -1 1;1 1 -1 -1 1;1 1 -1 -1 1;1 1 -1 -1 1;1 1 -1 -1 1]
Z = [0 0 0 0 0;1 1 1 1 1;2 2 2 2 2;3 3 3 3 3;4 4 4 4 4]
X'
subplot(1,2,1)
mesh(X,Y,Z)
subplot(1,2,2)
mesh(X',Y,Z)
至于plot3,这是其帮助文件的节选翻译:plot3(X1,Y1,Z1,...),X1,Y1,Z1是向量或者是矩阵,在坐标是X1,Y1,Z1的点画出一条或是多条空间中的直线。依旧用以上的实验看看plot3的效果,发现其实plot3是把矩阵对应列向量的点用直线连接起来的。(当然如果是行向量就另当别论了)
cylinder绘制旋转体
继续翻译啊翻译:[X,Y,Z] = cylinder(r)返回用r定义的侧面x,y,z坐标。cylinder认为r的每一个元素都是一个等高空间的半径。每个圆周被20等分。
[X,Y,Z] = cylinder(r,n)返回被向量r定义的侧面的x,y,z坐标。每个圆周被n等分。
由此可见,cylinder有一个局限,就是画出的图形的z坐标必然在0到1之间。例如帮助文件里的一个例子:
t = 0:pi/10:2*pi;
[X,Y,Z] = cylinder(2+cos(t));
surf(X,Y,Z)
axis square
然而可以使用缩放公式进行修正,比如,实际尺寸应该是从0到2*pi,那么就可以在画图以前对Z坐标进行修正:
t = 0:pi/10:2*pi;
[X,Y,Z] = cylinder(2+cos(t));
Z = Z*2*pi;
surf(X,Y,Z)
axis square tight vis3d
还可以考虑平移+改变方向:
t = 0:pi/10:2*pi;
[X,Y,Z] = cylinder(2+cos(t));
Z = Z*2*pi-pi;
surf(Z,X,Y)
axis square tight vis3d
这是效果图: