【决策单调性的动态规划】noi2009诗人小G

关于决策单调性在网上有一篇非常好的论文----<1D1D动态规划优化初步>.

 

O(N^2)的算法想必大家一定秒出了，可以发现这道题所用的方程是个经典1D1D方程：f[i]=min{f[j]+cost[i,j]}；

那么我们的任务就是证明决策单调性在直接套用模板即可，所谓决策单调性，就是我们要证明这样一个命题：

 

如果 f[k]的最优决策是j，f[k-1]的最优决策是i，（i<j），那么对于所有f[l](l>k),使用j转移都会比使用i转移优，对于所有f[l](l<=k)，使用i转移都会比使用j转移优。

 

首先我们可以得到的已知条件是使用i转移f[k]比使用j转移f[k]要优，j转移f[k+1]比使用i转移f[k+1]要优，经过一页纸的数学公式讨论以后，果断放弃了，发现使用数形结合更好解释。

 

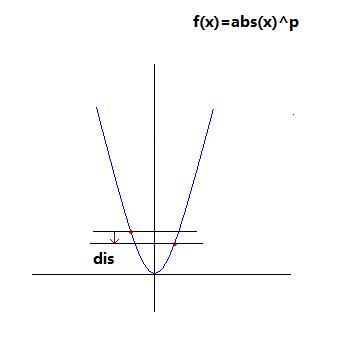
设cost[k,j]=|c[j]|^p,cost[k,i]=|c[i]|^p,首先可知c[j]-c[i]为定值(j>i),那么现在我们要证明的就是随着k的递增，|c[j]|^p-|c[i]|^p是一个单调的函数就可以了，我们把它映射到函数上：

对于k不断增大，可以发现dis=|c[j]|^p-|c[i]|^p是单调变化的(因为带了个绝对值所以不知道怎么求导。。寻找数学帝)

 

就这样解决了。

 

代码：

program ex2; const inf=1e18+1; var f,s:array[0..100000] of extended; l,r,fa,c:array[0..100000] of longint; a:array[0..100000] of ansistring; i,j,k,p,n,d,t,ll,rr,mm,task:longint; o:extended; ans:int64; function m(a:extended;i:longint):extended; begin m:=a;for i:=2 to i do m:=m*a end; function from(i,j:longint):extended; begin from:=f[j]+m(abs(s[i]-s[j]-o),p) end; procedure draw(i:longint);var j:longint; begin if i=0 then exit else draw(fa[i]); for j:=fa[i]+1 to i-1 do write(a[j],' '); writeln(a[i]); end; begin assign(input,'poet.in');reset(input); assign(output,'poet.out');rewrite(output); readln(task); for task:=1 to task do begin readln(n,o,p);o:=o+1; for i:=1 to n do begin readln(a[i]);s[i]:=s[i-1]+length(a[i]); end; for i:=1 to n do s[i]:=s[i]+i; d:=1;t:=1;l[1]:=1;r[1]:=n;c[1]:=0; for i:=1 to n do begin f[i]:=from(i,c[d]); fa[i]:=c[d];l[d]:=i+1; inc(d,ord(l[d]>r[d])); if from(n,i)>from(n,c[t])-0.9 then continue; while (t>=d)and(from(l[t],i)<from(l[t],c[t]))do dec(t); inc(t);l[t]:=r[t-1]+1;r[t]:=n;c[t]:=i; if t>d then begin ll:=l[t-1];rr:=l[t]; while ll<rr do begin mm:=(ll+rr)>>1; if from(mm,c[t-1])>from(mm,i) then rr:=mm else ll:=mm+1; end; r[t-1]:=ll-1;l[t]:=ll; end; end; if f[n]>inf then writeln('Too hard to arrange') else begin ans:=round(f[n]); writeln(ans); end; draw(n); writeln('--------------------'); end; close(input);close(output); end.