Rounding Methods(舍入模式)
What is "Rounding" ?
Rounding means reducing the digits in a number while trying to keep its value similar. The result is less accurate, but easier to use.
Example: 7.3 rounds to 7
Because 7.3 is closer to 7 than to 8
But what about 7.5? Is it closer to 7 or closer to 8? It is half-way in between, so what should we do?
Half Round Up (the common method of rounding)
The common method of rounding is to make 0.5 go up, so 7.5 rounds up to 8 (see Rounding Numbers).
7.5 usually rounds up to 8
But this is not a law or anything, it is just what people normally agree to do, and we get this:
- 7.6 rounds up to 8
- 7.5 rounds up to 8
- 7.4 rounds down to 7
Half Round Down
But 5 could go down if we wanted. In this case 7.5 would round down to 7, and we get this:
- 7.6 rounds up to 8
- 7.5 rounds down to 7
- 7.4 rounds down to 7
But you should let people know you are using "Half Round Down".
Why would you make 0.5 go down? Maybe you have lots of 0.5's in your numbers and want to see what rounding down would do.
Have a Play ... try different rounding methods on the Rounding Tool.
Negative Numbers
But what about -7.5?
- Does it round to -8 (and is that going "up" or "down" ?),
- Or does it round to -7
Help! I am confused!
In fact the whole world is confused about rounding negative numbers ... some computer programs round -7.5 to -8, others to -7
But we can agree here that "up" means heading in a positive direction, like on this number line:
Half Round Up (including negative numbers)
So we get this:
- 7.6 rounds up to 8
- 7.5 rounds up to 8
- 7.4 rounds down to 7
- -7.4 rounds up to -7
- -7.5 rounds up to -7
- -7.6 rounds down to -8
Half Round Down (including negative numbers)
If we were rounding 0.5 down we would get this:
- 7.6 rounds up to 8
- 7.5 rounds down to 7
- 7.4 rounds down to 7
- -7.4 rounds up to -7
- -7.5 rounds down to -8
- -7.6 rounds down to -8
"Symmetric" Rounding
But maybe you think "7.5 rounds up to 8, so -7.5 should go to -8", which is nice and symmetrical.
Well you are in luck because that is rounding towards or away from zero:
Round Half Away From 0
For this method, 0.5 rounds the number so it is further away from zero, like this:
- 7.6 rounds away to 8
- 7.5 rounds away to 8
- 7.4 rounds to 7
- -7.4 rounds to -7
- -7.5 rounds away to -8
- -7.6 rounds away to -8
Round Half Towards 0
Or you can have 0.5 round the number closer to zero, like this:
- 7.6 rounds away to 8
- 7.5 rounds to 7
- 7.4 rounds to 7
- -7.4 rounds to -7
- -7.5 rounds to -7
- -7.6 rounds away to -8
But Being Consistent Can Be Bad
Choosing any of those methods can be bad, though!
Especially if you have lots of 0.5s, like 5.5, 7.5, 6.5, 9.5, etc. The rounding would all be going in the same direction and you would have a bias.
So you can decide to round towards even (or odd) numbers! It works like this:
Round to Even
You round 0.5 to the nearest even digit
Example:
7.5 rounds up to 8 (because 8 is an even number)
but 6.5 rounds down to 6 (because 6 is an even number)
Other numbers (not ending in 0.5) round to nearest as usual, so:
- 7.6 rounds up to 8
- 7.5 rounds up to 8 (because 8 is an even number)
- 7.4 rounds down to 7
- 6.6 rounds up to 7
- 6.5 rounds down to 6 (because 6 is an even number)
- 6.4 rounds down to 6
- etc
Round to Odd
Just like "Round To Even", but 0.5 heads towards odd numbers
Example:
7.5 rounds down to 7 (because 7 is an odd number)
but 6.5 rounds up to 7 (because 7 is an odd number)
Round Randomly
You could also choose to round 0.5 up or down randomly, but how? By tossing a coin? Or a computer function?
With a large list of numbers this may give good results, but would give a different answer each time. Unless you used a fixed list of random choices.
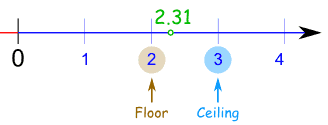
Floor and Ceiling
There are two other methods that don't even consider 0.5. They are called Floor and Ceiling.
Floor and ceiling give you the nearest integer up or down.
Floor
Using "floor", all digits go down, no matter what the dropped digit is:
Example: 7.8 goes down to 7
so does 7.2, 7.5, 7.9, etc.
And 7 goes to 7, too.
Ceiling
And "ceiling" goes up:
Example: 7.1 goes up to 8
so does 7.2, 7.5, 7.8, etc.
But 7 stays at 7.
Summary
| Number | Half Up |
Half Down |
Half Away 0 |
Half To 0 |
Half Even |
Half Odd |
Floor | Ceiling |
|---|---|---|---|---|---|---|---|---|
| 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
| 7.6 | 8 | 8 | 8 | 8 | 8 | 8 | 7 | 8 |
| 7.5 | 8 | 7 | 8 | 7 | 8 | 7 | 7 | 8 |
| 7.4 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 8 |
| 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 |
| -7 | -7 | -7 | -7 | -7 | -7 | -7 | -7 | -7 |
| -7.4 | -7 | -7 | -7 | -7 | -7 | -7 | -8 | -7 |
| -7.5 | -7 | -8 | -8 | -7 | -8 | -7 | -8 | -7 |
| -7.6 | -8 | -8 | -8 | -8 | -8 | -8 | -8 | -7 |
| -8 | -8 | -8 | -8 | -8 | -8 | -8 | -8 | -8 |
Rounding to Tens, Tenths, Whatever ...
In our examples we rounded to a whole number, but you can round to tens, or tenths, etc:
Example: "Half Round Up" to tens:
15 rounds up to 20
14.97 rounds down to 10
Example: "Half Round Up" to hundredths:
0.5168 rounds up to 0.52
1.41119 rounds down to 1.41
原文地址:http://www.mathsisfun.com/numbers/rounding-methods.html