R语言之方差分析篇

转载自：http://blog.csdn.net/lilanfeng1991/article/details/30753509

当包含的因子是解释变量时，通常会从预测转向 级别差异的分析，即称作方差分析（ANOVA）

组间因子

因变量

自变量

均衡设计（balanced design）

组内因子

单因素组间方差分析

单因素组内方差分析

重复测量方差分析

主效应

交叉效应

因素方差分析

混淆因素

干扰变数

协变量

协方差

1、ANOVA模型拟合

1.aov（）函数

语法：aov（formula,data=dataframe）

R表达式中的特殊符号

符号	用法
~	分隔符号，左边为响应变量，右边为解释变量 eg：y~A+B+C
+	分隔解释变量
：	表示变量的交互项 eg：y~A+B+A:B
*	表示所有可能交互项 eg：y~A*B*C可展开为：y~A+B+C+A:B+A:C+B:C+A:B:C
^	表示交互项达到次数 eg：y~(A+B+C)^2展开为：y~A+B+C+A:B+A:C+B:C
.	表示包含除因变量外的所有变量 eg：若一个数据框包括变量y,A、B和C，代码y~.可展开为y~A+B+C

常见研究设计的表达式

设计	表达式
单因素ANOVA	y~A
含单个协变量的单因素ANCOVA	y~x+A
双因素ANOVA	y~A*B
含两个协变量的双因素ANCOVA	y~x1+x2+A*B
随机化区组	y~B+A（B是区组因子）
单因素组内ANOVA	y~A+Error（Subject/A）
含单个组内因子（W）和单个组间因子（B） 的重复测量ANOVA	y~B*W+Error（Subject/W）

非平衡设计时或存在协变量时，效应项的顺序对结果影响较大

越基础的效应应越需要放在表达式前面，首先是协变量、然后是主效应、接着是双因素的交互项，再接着是三因素的交互项

若研究不是正交的，一定要谨慎设置疚的顺序

2、单因素方差分析 

（1）单因素方差分析

 #单因素方差分析（感兴趣地是比较分类因子定义的两个或多个组别中的因变量均值）
 install.packages("multcomp")
 library(multcomp)
 attach(cholesterol)
 str(cholesterol)
 cholesterol
 table(trt)
 aggregate(response,by=list(trt),FUN=mean)
 aggregate(response,by=list(trt),FUN=sd)
 fit<-aov(response~trt)
 summary(fit)
 library(gplots)
 plotmeans(response~trt,xlab="Treatment",ylab="Response",main="Mean Plot\n with 95%CI")

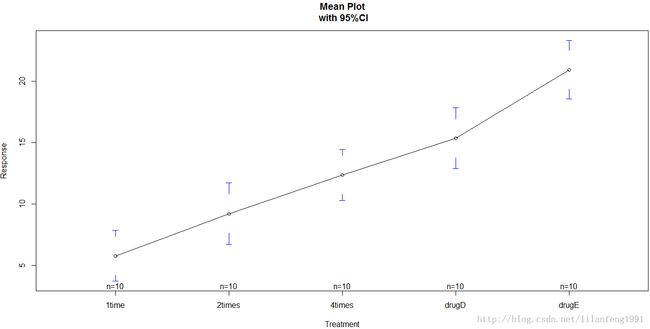
（2）多重比较

多重比较用于解决某一组别与其他的不同

TukeyHSD（）函数提供了对各组均值差异的成对检验，但与HH包存在兼容性问题(（某些版本中）；

 TukeyHSD(fit)
 par(las=2)
 par(mar=c(5,4,6,2))
 plot(TukeyHSD(fit))

 library(multcomp)
 par(mar=c(5,4,6,2))
 tuk<-glht(fit,linfct=mcp(trt="Tukey"))
 plot(cld(tuk,level=0.05),col="lightgrey")

（3）评估检验的假设条件

当因变量服从正态颁，各组方差相等时，可用Q-Q图来检验正态性假设

qqPlot（）要求用lm（）拟合，若数据落 在95%的置信区间范围内，说明满足正态性假设。

R提供的可以做方差齐性检验的函数

Bartlett检验bartlet.test（）

Fligner-Killeen检验 fligner.test（）

Brown-Forsythe检验

离群点检验

car包中的outlierTest（）函数来检测离群点

3、单因素协方差分析

 install.packages("multcomp")
 library(multcomp)
 head(litter,n=21)
 data(litter,package="multcomp")
 attach(litter)
 options(digits=5)
 table(litter$dose)
 aggregate(weight,by=list(litter$dose),FUN=mean)
 fit<-aov(weight~gesttime+litter$dose)
 summary(fit)

因使用了协变量，短途运输 获取调整的组均值即去除协变量疚后的组均值，可使用effects 包中的effects（）函数来计算调整的均值

 library(effects)
 effect("dose",fit)

用户定义的对照的多重比较

 library(multcomp)
 contrast<-rbind("no drug vs.drug"=c(3,-1,-1,-1))
 summary(glht(fit,linfct=mcp(dose=contrast)))

（1）评估检验的假设条件

ANCOVA与ANOVA相同，都城要正态性和同方差性假设

另ANOCVA还假定回归低低斜率相同，eg当ANCOVA模型饮食怀孕时间*剂量的交互项时，可对回归斜率的同质性进行检验。

eg

检验回归斜率的同质性

 library(multcomp)
 fit2<-aov(weight~gesttime*dose,data=litter)
 summary(fit2)

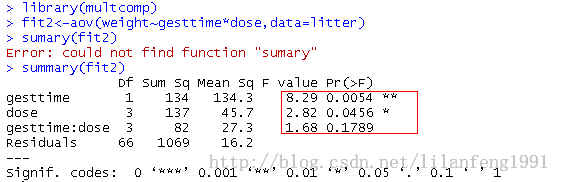
（2）结果的可视化

 install.packages("HH")
 library(HH)
 ancova(weight~gesttime+dose,data=litter)

4、双因素方差分析

 <strong>双因素ANOVA</strong>

 attach(ToothGrowth)
 head(ToothGrowth)
 table(supp,ToothGrowth$dose)
 aggregate(len,by=list(supp,ToothGrowth$dose),FUN=mean)
 aggregate(len,by=list(supp,ToothGrowth$dose),FUN=sd)
 fit<-aov(len~supp*ToothGrowth$dose)
 summary(fit)
 detach(ToothGrowth)

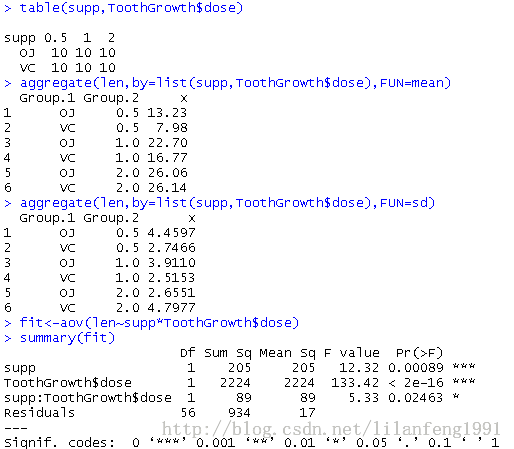
可视化处理

 interaction.plot(ToothGrowth$dose,supp,len,type="b",col=c("red","blue"),pch=c(16,18),main="Interaction between Dose and Supplement Type")

可用gplots包中的plotmans（）来展示交互效应

 install.packages("gplots")
 library(gplots)
 plotmeans(len~interaction(supp,ToothGrowth$dose,sep=" "),
           connect=list(c(1,3,5),c(2,4,6)),
           col=c("red","darkgreen"),
           main="Interaciton Plot with 95% CIS",
           xlab="Treatment and Dose Combination")

用HH包中的interaction2wt（）函数来可视化结果

 library(HH)
 interaction2wt(len~supp*ToothGrowth$dose)

5、重复测量方差分析

所谓重复测量方差分析，即受试者被测量不止一次。

 w1b1<-subset(CO2,Treatment=="chilled")
 w1b1
 fit<-aov(uptake~conc*Type+Error(Plant/(conc)),w1b1)
 summary(fit)
 par(las=2)
 par(mar=c(10,4,4,2))
 with(w1b1,interaction.plot(conc,Type,uptake,type="b",col=c("red","blue"),pch=c(16,18),
                           main="Interaction Plot for Plant Type and Concentration"))

 boxplot(uptake~Type*conc,data=w1b1,col=c("gold","green"),
         main="Chilled Quebec and Mississippi Plants",
         ylab="Carbon dioxide uptake rate umol/m^2 sec")

数据集

宽格式（wide format）：列是变量，行是观测值，且一行一个受试对象

处理重复测量设计时，需要有长格式（long format）数据才能拟合模型；在长格式中，因变量每次测量都要放到它独有的行中。reshape包可为人正直将数据转换为相应的格式。

6、多元方差分析

（1）单因素多元方差分析

 library(MASS)
 head(UScereal)
 attach(UScereal)
 y<-cbind(calories,fat,sugars)
 aggregate(y,by=list(shelf),FUN=mean)
 cov(y)
 fit<-manova(y~shelf)
 summary(fit)
 summary.aov(fit)

（2）评估假设检验

单因素多元方差分析有两个前提假设，一个是多元正态性，一个是方差-协方差同质性。前者可用Q-Q图来检验该假设条件；方差-协方差矩阵同持性即指各组的协方差矩阵相同，可用Box's M检验来估计该假设。

多元正态分布：若有一个p*1的多元正态随机向量x，均值为u，存在协方差矩阵，那么x与u的马氏距离的平方服从自由度为p的卡方分布。

Q-Q图展示卡方颁的分位数，横纵坐标分别是样本量与马氏距离平方值。如果点全部落在斜率为1、截距为0的直线上，则表明数据服从多元

正态分布。

 center<-colMeans(y)
 n<-nrow(y)
 p<-ncol(y)
 cov<-cov(y)
 d<-mahalanobis(y,center,cov)
 coord<-qqplot(qchisq(ppoints(n),df=p),d,main="Q-Q Plot Assessing Multivariate Normality",
               ylab="Mahalanobis D2")
 abline(a=0,b=1)
 identify(coord$x,coord$y,labels=row.names(UScereal))

可用mvoutlier包中的ap.plot（）函数来检验多元离群点

 install.packages("mvoutlier")
 library(mvoutlier)
 outliers<-aq.plot(y)
 outliers

（3）稳健多元方差分析

若多元正态性或者方差-协方差均值假设都不满足，又担心多元离群点，可考虑用稳健或非参版本的MANOVA检验。

rrcov包中的Wilks.test（）函数实现

vegan包中的adonis（）函数提供了非参数MANOVA的等同形式

 library(rrcov)
 Wilks.test(y,shelf,method="mcd")

7、用回归来做ANOVA

用aov（）函数拟合模型

 library(multcomp)
 levels(cholesterol$trt)
 fit.aov<-aov(response~trt,data=cholesterol)
 summary(fit.aov)

用回归lm（）来解决ANOVA问题

 fit.lm<-lm(response~trt,data=cholesterol)
 summary(fit.lm)

因线性模型要求预测变量是数值型，当lm（）函数碰到因子时，它会用一系列因子水平相对应的数值型对照变量为代替因子。若因子有k个水平，它将会创建k-1个对照变量。

 contrasts(cholesterol$trt)

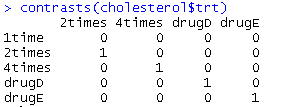
内置对照组

对照变量创建方法	描述
contr.helmert	第二个与第一个水平对照 第三个水平对照前两个均值 第四个水平对照前三个的均值
contr.poly	基于正交多项式的对照，用于趋势分析和等距水平的有序因子
contr.sum	对照变量之和限制为0，也称作偏差找对，对各水平的均值与所有水平的均值进行比较
contr.treatment	各水平对照基线水平，也称虚拟编码
contr.SAS	类似于contr.treatment，只是基线水平变成了最后一个水平

可通过contrasts选项，修改lm（）默认的对照方法

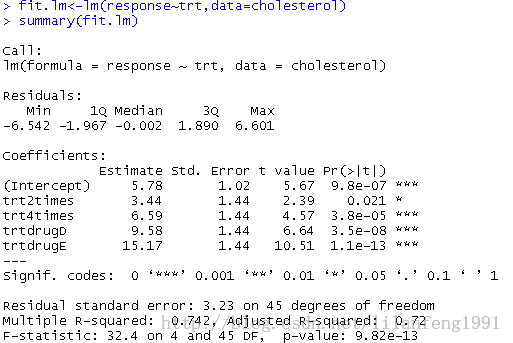
 fit.lm<-lm(response~trt,data=cholesterol,contrasts="contr.helmert")
 fit.lm

还可通过设定options（）函数修改R会话中的默认对照方法

eg：

options(contrasts=c(contr.SAS","contr.helmert"))