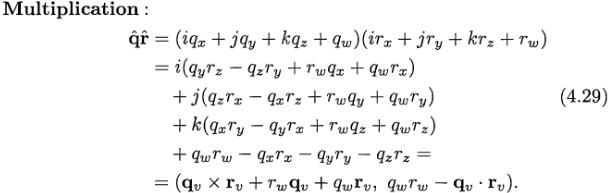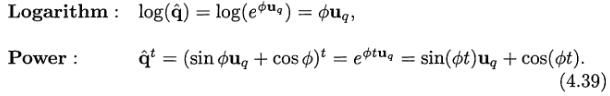实时渲染(第三版):第四章 转换 4.3.1
4.3 四元组
早在1843年,William Rowan Hamilton就发明了四元组作为复数的扩展;但直到1985年,四元组才被Shoemake引入到计算机图形学领域。它是一个强大的工具,可以用来构建拥有引人注目的特性的转换;并且,从某种意义上讲,它比欧拉角和矩阵更加优越(尤其是在旋转和方向上)。给定一个轴和角度,将之转换到四元组,或者反过来将四元组转换到一个轴和角度,是极其简单的;而任何方向上的欧拉角转换都是困难的。四元组可被用于稳定不变的方向插值(欧拉角无法很好地处理这件事情)。
复数有一个实部和一个虚部;它们都用一个实数表示,第二个实数被乘以![]() 。类似地,四元组拥有四个部分,前面的三个和旋转轴密切相关,含有旋转的角度,该角度将影响所有的四个部分(参考节4.3.2)。四元组用四个关联到不同部分的实数表示。我们选择用向量表示四元组,但是,为了区分它们,我们会添加…^符号:q^。我们从四元组的数学背景开始,然后用它来构造有趣又有偶用的转换。
。类似地,四元组拥有四个部分,前面的三个和旋转轴密切相关,含有旋转的角度,该角度将影响所有的四个部分(参考节4.3.2)。四元组用四个关联到不同部分的实数表示。我们选择用向量表示四元组,但是,为了区分它们,我们会添加…^符号:q^。我们从四元组的数学背景开始,然后用它来构造有趣又有偶用的转换。
4.3.1 数学背景
定义:四元组q^可用下面的方式定义,它们都是等价的:
变量qw被叫做四元组q^的实部,qv是虚部。i,j,k叫做虚数单位。
对虚部qv,我们可以使用所有普通的向量操作,如加、缩放、点积、叉积等。根据四元组的定义,两个四元组q^和r^的乘法操作可被展开为下面的形式。注意,虚数单位的乘法是不可交换的。
在公式中可以看到,我们使用了叉积和点积来计算四元组的乘积(实际上,四元组乘积是叉积和点积的来源)。根据四元组的定义,我们还需要加法、共轭、标准化和单位化:
当n(q^)=![]() 被简化(结果如上所示),虚部被抵消,只剩下实部。标准化有时表示为||q^||=n(q^)。上面的意义是可以导出乘法的逆元素(表示为q^-1)。公式q^-1q^ = q^q^-1 = 1必定持有逆元素(和普通数字类似)。 我们从标准化的定义派生了一个公式:
被简化(结果如上所示),虚部被抵消,只剩下实部。标准化有时表示为||q^||=n(q^)。上面的意义是可以导出乘法的逆元素(表示为q^-1)。公式q^-1q^ = q^q^-1 = 1必定持有逆元素(和普通数字类似)。 我们从标准化的定义派生了一个公式:
该公式给出了乘法的逆元素:
乘法逆元素公式中使用了和标量的乘法,它由公式4.29派生:sq^ = (0,s)(qv,qw) = (sqv,sqw), q^s = (qv,qw)(s,0) = (sqv,sqw)。这说明和标量相乘满足交换律:sq^ = q^s = (sqv,sqw)。
从定义还可导出下面的这些规则:
一个单位四元组q^ = (qv, qw), 其n(q^) = 1。根据这点,对于||uq|| = 1的三维向量,q^又可写作:
因为:
我们将在下一节看到,单位四元组特别适合于以最高效率的方式创建旋转和朝向。但在此之前,首先需要介绍一些单位四元组的操作。
对于复数,一个二维单位向量可以写作cosΦ + i sinΦ = eiΦ。对于四元组,等价公式为:
单位四元组的log和指数函数公式如下: