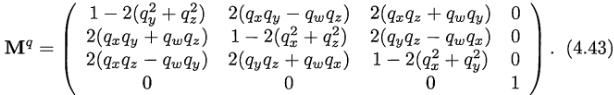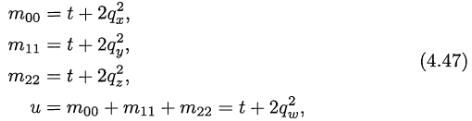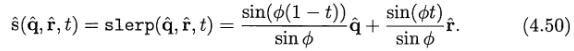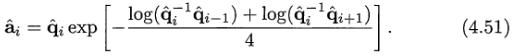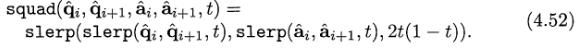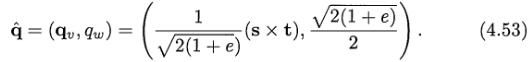实时渲染(第三版):第四章 转换 4.3.2
4.3.2 四元组转换
我们现在开始学习四元组的一个子类别,称为单位四元组,它们都是单位长度。单位四元组的最重要的事实是它们可以表示任何三维旋转,并且这种表示极其简洁简单。
现在,我们来看看单位四元组为啥对旋转和方向如此有用。首先,将拥有四个坐标的点或向量(p = (Px Py Pz Pw)T )放到四元组p^中,假设有一个单位四元组q^ = (sinΦuq, cosΦ)。那么:
![]()
将绕着轴uq旋转p^(也是点p)2Φ弧度。注意,既然q^是一个单位四元组,那么q^-1 = q^*。它可以用于绕着任意轴的旋转,如图4.8所示。
图 4.8 单位四元组表示的旋转转换演示。单位四元组q^ = (sinΦuq, cosΦ)。该转换绕着uq旋转2Φ弧度.
任何非0实数和q^的乘积也表示同样的转换,这意味着,q^和-q^表示同样的旋转。也就是说,将轴uq反向,将实部qw取负,产生的四元组在转换上和原四元组效果相同。它还表示,从矩阵提取四元组,可以返回q^或-q^。
给定两个单位四元组q^和r^,假设它们的串联为首先应用q^,然后是r^,最后是应用的对象p^(可当作点p),则可用公式4.41表示:
![]()
此处,c^ = r^q^,它也是单位四元组,表示的是单位四元组q^和r^的串联。
矩阵转换
某些系统上矩阵乘法实现于硬件,并且矩阵乘法比公式4.40更高效,因此,我们需要将四元组和矩阵进行互转的方法。四元组q^,转换到矩阵Mq的公式如4.42:
此处,标量是s = 2/n(q^)。对于单位四元组,它可以简化为:
四元组构建好之后,就无需再进行三角函数的计算。
将正交矩阵Mq转换到单位四元组q^,稍微复杂点。它的关键如公式4.44,和公式4.43有所不同:
这些等式的含义是,如果qw已知,可以求出向量vq的值,进而可以导出q^。Mq的迹如下计算:
该结果将为单位四元组产生下面的转换:
为拥有数值稳定的事务,应当避免被小数相除。因此,首先设置![]() ,接着,
,接着,
可以判断出m00,m11,m22中的最大值,而u决定qx, qy, qz, 和 qw中的最大值。如果qw是最大的,则可用公式4.46导出四元组。否则,首先使用下面的公式计算qx, qy, qz中的最大值:
之后,使用公式4.44计算q^的其他部分。幸运的是,有这个计算的代码(参考进一步阅读和资源)。
球形线性插值
给定两个单位四元组(q^和r^)和一个参数t∈[0,1],球形线性插值可以计算一个插值四元组。这对对象动画有用;但对相机方向,就没有在插值期间倾斜相机朝上向量(通常是一种干扰效果)那般有用。
该操作的代数形式可被表示为下面的复合四元组s^:
s^(q^,r^,t) = (r^q^-1)tq^ (4.49)
不过,对于软件实现,下面的形式会更加适合(其中,slerp表示球形线性插值):
为计算Φ,可以使用下面的等式:cosΦ = qxrx + qyry + qzrz + qwrw。t∈[0,1],slerp函数计算(唯一(当且仅当q^和r^非反))插值四元组,这些四元组构成了四维单位球体上、从q^(t=0)到r^(t=1)的最短弧。该圆弧所在的圆形成于q^,r^和原点指定的平面和四维单位球体间的交叉点,如图4.9所示。算出的旋转四元组绕着固定轴已恒定速度旋转。这种拥有恒定速度、不会有加速度的曲线,被叫做测地线。
图 4.9 单位四元组表示为单位球体上的点。slerp函数用来在四元组之间进行插值,插值路径是球体上的弧。注意,从q1^到q2^的插值和从q1^到q3再^到q2^的插值不是一回事(虽然它们达到相同的方向)。
slerp函数相当适合于两个方向间的插值,其表现很好(固定轴,恒定速度)。但使用欧拉角进行插值时就不是这样。在实践中,直接计算slerp是个昂贵的操作,它需要调用三角函数。Li提供了更快的增量方法,并且不会牺牲任何精度。
当存在两个以上的方向,假设为q0^,q1^,...qn-1^,并且,我们想要从q0^到q1^到q2^...直到qn-1^,进行插值,那么就可以简单的方式使用slerp。现在,假设我们进行到了qi^,那么可以使用qi^和qi-1^作为参数计算slerp。之后,使用qi^和qi+1^。这将导致突然抖动出现于方向插值中。这点和点的线性插值类似;参考图13.2右上角。
更好的插值方法是使用某种类型的样条线。在qi^和qi+1^之间引入ai^和ai+1^,则可使用它们定义球形立方体插值。让人惊奇的是,这些额外的四元组被如下计算:
qi^和ai^将被用于球形插值四元组,使用一个平滑的立方体样条线,入公式4.52:
从上面的公式可以看出,squad函数构建于重复的球形插值(使用slerp)。插值传递初始的方向,qi^,i∈[0,...,n-1],但不会传递ai^(它们被用来表示初始方向的切方向)。
从一个向量旋转到另一个
一个常用的操作是从方向s转换到另一个方向t,尽可能用最短的路径。四元组大大简化了这一过程,从这也可以看出四元组和它的密切关系。首先,标准化s和t。然后,计算单位旋转轴,假设叫u:u = (s×t)/||s×t||。接着,e = s.t = cos(2Φ),||s×t|| = sin(2Φ),其中2Φ是s和t之前的夹角。则,表示从s旋转到t的四元组为q^ = (sinΦu, cosΦ) =![]() ,用半角关系和三角恒等式简化后为:
,用半角关系和三角恒等式简化后为:
以这种方式(相比于标准化点积s×t)直接生成四元组可避免s,t相隔很近时的数值不稳定。但当s和t在相反的方向时,两种方法都存在不稳定问题,因为会发生被0除。这种特殊情况下,垂直于s的旋转轴可用于旋转t。
有时,我们需要从s旋转到t的矩阵表示。公式4.43在一些代数和三角简化后,旋转矩阵变成为:
在这个公式中,我们使用了下面的中间计算:
如你所见,所有的方根和三角函数都被简化消去,这是创建矩阵的高效方法。
注意,当s和t是平行或接近平行时,你要特别小心,因为此时||s×t||≈0。如果Φ≈0,那么我们可以返回单位矩阵。如果2Φ≈π,那么我们可以绕着任一轴旋转π弧度,该任一轴可通过s和另一不平行与s的向量的叉积获得。Moller 和 Hughes 使用豪斯霍尔德矩阵(Householder matrices)处理这个特例。
示例:定位和定向相机
假设虚拟相机(或视点)的默认位置是(0 0 0)T,默认的视图方向v沿着-z轴,如v = (0 0 0)T。现在,目标是创建一个转换,将相机移动到一个新的位置p,看向方向w。从定向相机开始,旋转默认视图方向到目标视图方向,由R(v, w)负责。定位只要简单地平移到p。于是,产生的结果转换为X = T(p)R(v, w)。在实际使用中,第一个旋转之后,往往需要另一个向量到向量的旋转转换,以旋转视图上方向到某个需求的朝向。