图像处理:基础(模板、卷积运算)
模板:矩阵方块,其数学含义是一种卷积运算。
卷积运算:可看作是加权求和的过程,使用到的图像区域中的每个像素分别于卷积核(权矩阵)的每个元素对应相
乘,所有乘积之和作为区域中心像素的新值。
卷积核:卷积时使用到的权用一个矩阵表示,该矩阵与使用的图像区域大小相同,其行、列都是奇数,
是一个权矩阵。
卷积示例:
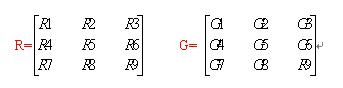
3 * 3 的像素区域R与卷积核G的卷积运算:
R5(中心像素)=R1G1 + R2G2 + R3G3 + R4G4 + R5G5 + R6G6 + R7G7 + R8G8 + R9G9
2.使用模板处理图像的问题:
边界问题:当处理图像边界像素时,卷积核与图像使用区域不能匹配,卷积核的中心与边界像素点对应,
卷积运算将出现问题。
处理办法:
A. 忽略边界像素,即处理后的图像将丢掉这些像素。
B. 保留原边界像素,即copy边界像素到处理后的图像。
如果你刚刚接触图像处理,或者离开大学很长时间,一看到卷积这个东西,肯定和我一样感到晕菜.那么就复习一下,并且实际的写个程序验证一下,我保证你这辈子不会再忘记卷积的概念了.我们来看一下一维卷积的概念.
连续空间的卷积定义是 f(x)与g(x)的卷积是 f(t-x)g(x) 在t从负无穷到正无穷的积分值.t-x要在f(x)定义域内,所以看上去很大的积分实际上还是在一定范围的.
实际的过程就是f(x) 先做一个Y轴的反转,然后再沿X轴平移t就是f(t-x),然后再把g(x)拿来,两者乘积的值再积分.想象一下如果g(x)或者f(x)是个单位的阶越函数. 那么就是f(t-x)与g(x)相交部分的面积.这就是卷积了.
把积分符号换成求和就是离散空间的卷积定义了.那么在图像中卷积卷积地是什么意思呢,就是图像就是图像f(x),模板是g(x),然后将模版g(x)在模版中移动,每到一个位置,就把f(x)与g(x)的定义域相交的元素进行乘积并且求和,得出新的图像一点,就是被卷积后的图像. 模版又称为卷积核.卷积核做一个矩阵的形状.
卷积定义上是线性系统分析经常用到的.线性系统就是一个系统的输入和输出的关系是线性关系.就是说整个系统可以分解成N多的无关独立变化,整个系统就是这些变化的累加.
如 x1->y1, x2->y2; 那么A*x1 + B*x2 -> A*y1 + B*y2 这就是线性系统. 表示一个线性系统可以用积分的形式 如 Y = Sf(t,x)g(x)dt S表示积分符号,就是f(t,x)表示的是A B之类的线性系数.
看上去很像卷积呀,,对如果f(t,x) = F(t-x) 不就是了吗.从f(t,x)变成F(t-x)实际上是说明f(t,x)是个线性移不变,就是说 变量的差不变化的时候,那么函数的值不变化. 实际上说明一个事情就是说线性移不变系统的输出可以通过输入和表示系统线性特征的函数卷积得到.
一:什么是卷积
离散卷积的数学公式可以表示为如下形式:
f(x) = - 其中C(k)代表卷积操作数,g(i)代表样本数据, f(x)代表输出结果。
举例如下:
假设g(i)是一个一维的函数,而且代表的样本数为G = [1,2,3,4,5,6,7,8,9]
假设C(k)是一个一维的卷积操作数, 操作数为C=[-1,0,1]
则输出结果f(x)可以表示为 F=[1,2,2,2,2,2,2,2,1] //边界数据未处理
以上只是一维的情况下,当对一幅二维数字图像加以卷积时,其数学意义可以解释如下:
源图像是作为输入源数据,处理以后要的图像是卷积输出结果,卷积操作数作为Filter
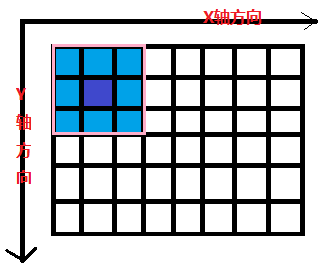
在XY两个方向上对源图像的每个像素点实施卷积操作。如图所示:
粉红色的方格每次在X/Y前进一个像素方格,就会产生一个新的输出像素,图中深蓝色的代
表要输出的像素方格,走完全部的像素方格,就得到了所有输出像素。
图中,粉红色的矩阵表示卷积操作数矩阵,黑色表示源图像– 每个方格代表一个像素点。
二:卷积在数字图像处理中应用
一副数字图像可以看作一个二维空间的离散函数可以表示为f(x, y), 假设有对于二维卷积操
作函数C(u, v) ,则会产生输出图像g(x, y) = f(x, y) *C(u,v), 利用卷积可以实现对图像模糊处理,边缘检测,产生轧花效果的图像。
一个简单的数字图像卷积处理流程可以如下:
1. 读取源图像像素
2. 应用卷积操作数矩阵产生目标图像
3. 对目标图像进行归一化处理
4. 处理边界像素
三使用模板处理图像相关概念:
模板:矩阵方块,其数学含义是一种卷积运算。
卷积运算:可看作是加权求和的过程,使用到的图像区域中的每个像素分别于卷积核(权矩阵)的每个元素对应相
乘,所有乘积之和作为区域中心像素的新值。
卷积核:卷积时使用到的权用一个矩阵表示,该矩阵与使用的图像区域大小相同,其行、列都是奇数,
是一个权矩阵。
卷积示例:
3 * 3 的像素区域R与卷积核G的卷积运算:
R5(中心像素)=R1G1 + R2G2 + R3G3 + R4G4 + R5G5 + R6G6 + R7G7 + R8G8 + R9G9

四使用模板处理图像的问题:
边界问题:当处理图像边界像素时,卷积核与图像使用区域不能匹配,卷积核的中心与边界像素点对应,
卷积运算将出现问题。
处理办法:
A. 忽略边界像素,即处理后的图像将丢掉这些像素。
B. 保留原边界像素,即copy边界像素到处理后的图像。
六其他
-----------------------------------------------------------------------------------------------------------
以下用$符号表示从负无穷大到正无穷大的积分。
一维卷积:
y(t)=g(k)*x(k)=$g(k)x(t-k)
先把函数x(k)相对于原点反折,然后向右移动距离t,然后两个函数相乘再积分,就得到了在t处的输出。对每个t值重复上述过程,就得到了输出曲线。
二维卷积:
h(x,y)=f(u,v)*g(u,v)=$$f(u,v)g(x-u,y-v)
先将g(u,v)绕其原点旋转180度,然后平移其原点,u轴上像上平移x, v轴上像上平移y。然后两个函数相乘积分,得到一个点处的输出。
在图像中卷积是什么意思呢,就是图像就是图像f(x),模板是g(x),然后将模版g(x)在模版中移动,每到一个位置,就把f(x)与g(x)的定义域相交的元素进行乘积并且求和,得出新的图像一点,就是被卷积后的图像.模版又称为卷积核.卷积核做一个矩阵的形状。由于大多数模板都是对称的,所以模板不旋转。
-----------------------------------------------------------------------------------------------------------