对一道面试题的总结与扩展思考（关于一笔画问题的数学分析）

 

摘要

前几天参加了一个公司的面试，其中被问到了一个题。面试官在纸上画了一个图形（具体图形见下文），问我能不能一笔画出这个图形，要求每条边必须只走一次，并且画的过程中笔不能离开纸。当时我没有试着去画 ，而是凭着自己图论方面的知识在几秒钟之内告诉面试官不可能做到，然后简单说了一下理由。面试结束后我翻阅了图论相关的资料，发现当时自己虽然给出了正确答案，但理由并不完全正确。昨天我花了几个小时仔细研究了一下相关的理论，总结了一下这类问题的类型和解法，写成此文，分享给大家。

问题的提出

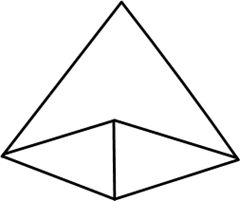
当时面试官给我出的问题是这样的：对于下面这个图形，让我一笔画出，要求每条边必须只走一次，并且画的过程中笔不能离开纸。

面试时我给出的回答是不可能做到，面试结束后我也从数学上证明了这个这个回答。当然有兴趣的朋友可以试着画画看。

这个问题其实就是我们小时候会玩到的一笔画游戏。这类问题看似简单直观，但是仔细研究下来却蕴含了很多东西，而且涉及了图论中一个非常重要的研究课题——欧拉迹。而且这类问题可以扩展出很多东西，例如任意给一个图可不可以完成一笔画且最后回到起始点？再如到底什么样的图可以一笔画出来？什么样的图一笔画不出来？如果一个图可以一笔画出来，那么应该如何画？有没有对一切可一笔画图形的通用解法？

下面我们将这个问题抽象成一般问题，然后从图论角度寻找上述疑问的答案。

图论中的一些概念

因为在下文论述过程中需要用到一些图论的基本概念，为了照顾在这方面不熟悉的朋友，我先将要用到的定义和概念列出来，如果您对图论的基本内容已经了然于胸，可以跳过这一节。另外如不做特殊说明，下文所有的“图”都默认指“无向图”，本文的讨论不涉及“有向图”。

简单图——一个简单图可表示为G=(V, E)，其中V是顶点集合，其中每个元素是图的一个顶点；E是边集合，其中每一个的元素是一个顶点对(a, b)，其中a和b均属于V，这个顶点对表示顶点a和b间有一条边相连。

多重图——简单图不允许同一组顶点对在E中出现两次，即一对顶点间最多只有一条边。如果在简单图的基础上允许任一组顶点对间有任意条边，则简单图变为多重图。

一般图——如果在多重图的基础上允许自关联边，即允许(a, a)这样的顶点对出现在E中，则这种图叫一般图。（我们后续所有讨论的对象都是一般图，如不做特殊说明，下文所有的“图”均指一般图）

顶点的度——一个顶点的度是这个顶点所连接的边的条数。

连通图——如果一个图任意两个顶点之间都存在由边组成的通路，则这种图叫连通图。（我们后续所有讨论的对象都是连通图，如不做特殊说明，下文所有的“图”均指无向一般连通图）

途径——在一个图G中，{x1, x2}, {x2, x3}, …, {xm-1, xm}叫做G的一个途径，如果x1和xm为同一顶点，则说这个途径是闭的，否则说这个途径是开的。

迹——如果一个途径中没有重复的边，则这个途径叫做“迹”。

欧拉迹——如果图G的一个迹包含了G所有的边，则这个迹叫做“欧拉迹”。

一笔画问题的抽象

有了上面的定义，我们就可以用数学语言描述一笔画问题了：

所谓一笔画问题，就是给定一个无向一般连通图，这个图存在欧拉迹的充分必要条件是什么？如果存在欧拉迹，如何求欧拉迹？

这个问题很庞大，我们化整为零，分几步去讨论。另外，为了避免枯燥无味，我将不会从绝对严格的数理层面去做推理和证明，而是用一些直观的启发式方法，尽量让每位朋友都能读懂。

问题一：图G存在欧拉迹的必要条件是什么？

首先，我们来推导G存在欧拉迹的必要条件。虽然满足必要条件不能充分证明G一定存在欧拉迹，但是不满足必要条件就一定不存在欧拉迹。所以搞清这个问题，可以用来帮助我们判断出显然不能一笔画出的图。

欧拉迹分为开欧拉迹和闭欧拉迹，我们先讨论开欧拉迹的情况。

现已知图G存在开欧拉迹（等价于存在一笔画画法，并且这种画法在完成时不会回到起始顶点），那么可以推导出什么？

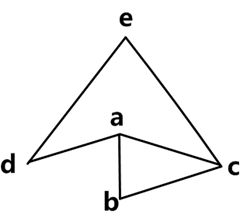
现在我们这样想：设{x1, x2}, {x2, x3}, …, {xm-1, xm}是G的一条开欧拉迹，那么{x1, x2, …, xm}是这条欧拉迹所经过的顶点的序列。需要注意，这里除了x1和xm一定不是同一顶点，其它很多顶点可能是相同的。因为欧拉迹只要求每个边出现且仅出现一次，但不限制同一顶点出现几次。例如下图：

其中{a, b}, {b, c}, {c, a}, {a, d}, {d, e}, {e, c}是一个开欧拉迹，顶点序列为{a, b, c, a,d, e, c}。

现在我们这么考虑这个问题，对于某一顶点x，I(x)表示欧拉迹中进入x的次数，即走整个欧拉迹过程中从x以外的顶点进入x顶点的次数，O(x)，表示离开x的次数，即当前在x顶点，然后离开x到其它顶点的次数。

我们顺着开欧拉迹走，对于所有顶点此时I(x)和O(x)均为0，当前笔触在x1处。

当从x1走到x2，O(x1)变为1，而I(x2)变为1。我们可以想象，除起始顶点和终止顶点外，其它顶点当走完这个欧拉迹时，I(x)一定等于O(x)，因为对于这些顶点，一次进入必然对应着一次离开。而起始顶点的不同在于，它多一次离开（第一步），所以I(x1)+1=O(x1)，同理，终止顶点多一次进入（最后一步），I(xm)=O(xm)+1。

我们还体会到这样一个事实：对于任意顶点，每一个进入和每一个离开都消耗此顶点的一个度。因为欧拉迹不允许重复边，所以每一次进入和离开一定是走以前没有走过的边，因此顶点x的度为I(x)+O(x)。这样可以得出结论：如果G存在一个开欧拉迹，那么起始顶点和终止顶点的度数为奇数，而其它顶点的度数为偶数。

再来考虑G存在闭欧拉迹的情况。根据上述思路，如果欧拉迹时闭的，则起始顶点和终止顶点为一个顶点，而这个顶点刚好多一个进入（最后），多一个离开（开始），这么一加，这个顶点的度也一定为偶数，其它顶点的度的推理与开欧拉迹相同。所以可以得出结论：如果G存在一个闭欧拉迹，那么G所有顶点的度均为偶数。

综上可以得出，一个图G存在欧拉迹的必要条件是所有顶点的度数均为偶数或恰好有两个顶点度数为奇数。从逻辑上说，如果一个命题成立，则其逆否命题也成立，我们可以得到推论：如果一个图G不是所有顶点都具有偶数度，也不是恰好有两个顶点为奇数度，则G一定不存在欧拉迹。

现在我们再来看看最初的那个面试题：那个图有四个顶点的度为3，所以根据上述分析，那个图一定不存在欧拉迹，即不可能一笔画出。

问题二：图G存在欧拉迹的充分条件是什么？

上图我们只证明了条件的必要性，这只能告诉我们如何判断一个图不存在欧拉迹，那么如果一个图所有顶点都是偶数度或恰好有两个顶点是奇数度，那么是否可以确定这个图存在欧拉迹呢？也就是说，问题一中的条件是否是充分的？

不卖关子，我很高兴的告诉大家，那个条件确实是充分的。也就是说，一个无向一般连通图G存在欧拉迹的充分必要条件是G中所有顶点均具有偶数度或恰好有两个顶点具有奇数度。但是这个定理的数理证明十分复杂，我实在没有兴趣在这里证明，因为我相信大家一定没有兴趣看一堆公式。因此，我放弃对充分性进行数理证明。这个证明过程可以在机械工业出版社的《组合数学》（Richard A. Brualdi著）一书的第302-303页找到，有兴趣的朋友请参看。

问题三：如果图G存在欧拉迹，如何求解？

知道了判断欧拉迹存在性的充要条件，下面一个问题自然就是如果G存在欧拉迹，如何找出？

这个算法相当简单：

1、设顶点集合W，边集合F，均初始化为空集。

2、选择一个奇数度点（开欧拉迹）或任意顶点（闭欧拉迹）赋值给x，并将x放入W。

3、如果所有边都已进入F则终止，否则进入4。

4、选择x连接的一条不存在于F中的边(x, y)，将(x, y)放入F，将y放入W（如果y不存在于W的话），然后让x=y。

5、回到3。

算法十分直观，就不多做解释，关于算法的正确性证明，有兴趣的朋友请参考上文提到《组合数学》一书中的第301页。

总结

下面总结一下一笔画问题相关的几个定理，记住这些，一笔画问题应该就难不倒你了。

1、一个无向一般连通图G可以一笔画出的充分必要条件是G中所有顶点均具有偶数度或恰好有两个顶点具有奇数度。

2、一个无向一般连通图G可以一笔画出且终止点不是起始点的充分必要条件是G中恰好有两个顶点具有奇数度。

3、一个无向一般连通图G可以一步画出且最后回到初始点的充分必要条件是G中所有顶点均具有偶数度。

4、如果一个无向一般连通图G不是所有顶点都具有偶数度，也不是恰好有两个顶点为奇数度，则G一定不存在欧拉迹。

扩展阅读

其实对一笔画问题的最早研究可以追溯到欧拉（Leonhard Paul Euler）在1736年发表的一篇关于哥德堡七桥问题的论文。那篇论文中欧拉解决了著名的哥德堡七桥问题，并且开创了一个全新的数学分支——图论与拓扑学。有兴趣的朋友可以寻找相关材料阅读。