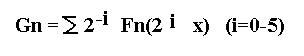用GPU实现Cellular Texture

转载请注明：来自 http://blog.csdn.net/skyman_2001

一、介绍

Steven Worley 在 Siggraph96 上发表的论文《 A Cellular Texture Basis Function 》提出了一种用于实现 cellular texture 的基函数。它们是基于分散“特征点 (feature point) ”到 R³ 空间，并建立基于局部点的分布的一个标量函数。这个函数的优点是不需要预计算或表存储。

二、第 n 最近点基函数

在 R³ 空间随机分布特征点。对任一位置 x ，定义 F₁(x) 为 x 到其最近特征点的距离。当 x 变化时， F₁ 平滑变化（因为 x 是平滑变化的）。但在特定端点， x 可能会与 2 个特征点的距离相等。但这是没关系的。 x 连续变化时， F₁ 值仍然连续，尽管 F₁ 的导数在计算距离从一特征点转到相邻特征点时会变化不连续。

F₂(x) 表示 x 与第 2 近的特征点的距离。同样，可定义 F_n(x) 为 x 到第 n 近的特征点的距离。 F 函数有如下有趣的特征：
      1. F_n 总是连续的；

2. F_n 是非减函数： 0<=F₁(x)<=F₂(x)<=F₃(x)… ，通常 F_n(x)<=F_n+1(x);

3. F_n 的梯度为从第 n 最近特征点到 x 的单位方向向量。
三、计算 F_n

为计算函数 Fn ，我们必须定义特征点如何在空间中分布。点的密度和分布将改变基函数的特性。我们想要点的同向性分布，以避免明显的格子状的形式。

最简单的分布是泊松分布。它指定空间中点的平均密度。每个点的位置独立于其他点。某一区域的点的竖立＝点的密度×该区域的体积（可能或多或少不一样）。每个区域的点的任何数目的确切概率可用离散泊松分布函数来计算。

一种方法是：将空间分为统一的立方体的格子。在整数坐标位置处分割。空间中的每个立方体可唯一的由其整数坐标表示，并且通过简单的 floor 操作，我们就可以确定。比如，点 (1.2,3.33,2.3) 位于由 (1,3,2) 索引的立方体内。

空间中的每个立方体可能包含 0 、 1 或多个特征点。我们可以实时地确定，因为泊松分布的随机分布函数描述了一立方体中每个可能的特征点数目的确切概率。对每个立方体的特征点的平均密度λ， m 个点在同一立方体的概率为 ( λ ^-m e ^λ m!)^-1 ，这样我们就可以列出 m=0,1,2,3… 的概率，并索引一随机数到该表中来确定在该立方体中有多少特征点。
    我们用随机数生成器产生的第 1 个值作为不同特征点数概率表的索引来找该立方体中的特征点数。

接下来，我们计算 m 特征点的位置（这是随机的，但对每个立方体是固定不变的）。我们用已经初始化了的随机数生成器来计算每个特征点的 XYZ 位置。这些坐标相对于立方体的底，且每个坐标分量都在 0~1 之间。

当我们产生这些点，我们计算它与初始函数计算位置 x 的距离，并保持一个目前第 n 近距离的排序表。这样就找到最近特征点和当前立方体空间中的点的值 F_n 。但是，相邻立方体的特征点中很有可能包含比我们发现的点更近的特征点，因此我们必须也在边界立方体中迭代。

四、 Cellular Texture 的应用

1. 最简单的情形—— F₁(x) ：
       在每个特征点周围放射状增加。效果就是在每个特征点周围放置斑点。这可以用来模拟圆点花样的布料等效果；

2. F₂(x) 和 F₃(x) ：

两者相组合可以产生更有趣的形式。如
                     F₂(x) – F₁(x)
    这种组合在 F₁=F₂ 时其值为 0 ，这发生在 Voronoi 边界。这可以用来模拟脉络状的窗饰等效果；
3. C₁F₁+C₂F₂+C₃F₃+C₄F₄ ：
       这是 F₁~F₄ 的线性组合。改变系数 C₁,C₂,C₃,C₄ 的值可以产生丰富多彩的迷人效果。超过 4 个 F 函数的组合，其产生的效果的差别就不明显了。所以这种组合一般控制在 4 个 F 函数之内；

4. 不规则碎片形（ fractal ）：
    其公式为
           
       使用 Gn 作为颜色的索引。
       其中， F1(x) 的 fractal 版本是最有用的：

             
                 

五、 GPU 实现

       本例子是用 Pixel Shader 实现 2D 的 Cellular Texture 。基本思路是 ， 由 CPU 计算随机数数组 ， 然后传给 GPU ， GPU 根据这些随机数对各个 cell 的中心点（也就是“特征点”）进行扰动，如下图所示，然后计算 F_n 。

                    

HLSL 源代码如下：

/////////////////////////////////////////////////////////

// File: cellulareffect.txt

//

// Author: Skyman (http://blog.csdn.net/skyman_2001)

//

// System: WinXP + Pentium D 2.66GHz + GeForce 7300 

//

// Desc: Cellular texture shader in an effect file.

//         

/////////////////////////////////////////////////////////

//

// Macros

//

#define Width 256

#define CellSize 32

 

//

// Globals

//

extern float NoiseArray[162];

 

//

// PS

struct vertout

{

   float2 HPos : VPOS;

};

 

struct fragout

{

   float4 col    : COLOR0;

};

 

fragout PSMain(vertout In)

{

   fragout Out;

  

   float a,b,f1,f2,f3;

   float2 CellCenter;

   float dist,shortest1,shortest2,shortest3;

   float dist2,s2;

   shortest1=shortest2=shortest3=10000;

   s2=10000;

   float n=0;

   for(a=0;a<=Width;a+=CellSize)

   {

      for(b=0;b<=Width;b+=CellSize)

      {

        CellCenter.x=a+NoiseArray[n];

        CellCenter.y=b+NoiseArray[n+1];

        n+=2;

       

        dist=distance(CellCenter,In.HPos);

        dist2=distance(CellCenter,In.HPos*2);

             

        if(dist<shortest1)

        {

           shortest3=shortest2=shortest1;

           shortest1=dist;

        }

        else if(dist<shortest2)

        {

           shortest3=shortest2;

           shortest2=dist;

        }

        else if(dist<shortest3)

           shortest3=dist;

          

        if(dist2<s2)

           s2=dist2;

      }

   }

   f1=clamp(shortest1,0,Width)/CellSize; // F1

   f2=clamp(shortest2,0,Width)/CellSize; // F2

   f3=clamp(shortest3,0,Width)/CellSize; // F3

   s2=clamp(s2,0,Width)/(Width*2);

   float f123=f3-0.25*f2-0.5*f1; // C1F1+C2F2+C3F3

   float f1frac=f1+0.5*s2; // F1 fractal (i=1)

   float f12=f2-f1; // F2-F1

   float mulf=f1*f2; // F1*F2

   float InvMulf=1-f1*f2; // 1-F1*F2

   float mulf2=f1*f2*f3; // F1*F2*F3

   Out.col=float4(f1,f1,f1,1.0);               

   return Out;  

}                       

 

//

// Effect

//

 

technique Cellular

{

    pass P0

    {      

       pixelShader = compile ps_3_0 PSMain();

    }

}

六、运行效果

1. F₁ ：                                                               2. F2：         

      

3. F3 ：                                                              4. F3-0.25*F2-0.5*F1 ：

      

5. F2-F1 ：                                                        6. F1*F2 ：

      

7. 1-F1 ：                                                          8. 1-(F2-F1) ：
      

9. 1-F1*F2 ：                                                   10. F1*F2*F3 ：

  

11.F2+F1-F3：                12.(F2-F1)/F1：
  

13.0.5×F1/(F2-F1)：              14.1-(F2-F1)/F1：

  

七、结束语

       Cellular Texture 是一项很有用的技术，可以用于过程纹理的创建（ 2D 和 3D ）。看到了吧， Cellular Texture 能产生许多有趣的图案。有兴趣的同志可以自己挖掘，产生比这更加丰富多彩的纹理效果。 Try it now!
       我的 MSN 是： [email protected] ， QQ ： 175910174 ，欢迎交流！