深入理解KMP算法

介绍

KMP算法是字符串匹配算法领域的一个经典算法, 由Knuth、Morris、Pratt三人提出,匹配复杂度是线性的,但是非常晦涩,初看不容易看明白,特别是next函数的计算.本文详细讲述KMP算法的具体原理和实现,并给出C++实现.

 

本文用到的标记

目标串: T[0,1,2….(n-1)] 长度为n

模式串: P[0,1,2….(m-1)] 长度为m

匹配失败时模式串序号返回的位置:next[0,1,2…m] 长度为m

 

内容

1.       朴素匹配算法

在讲述KMP之前,首先要理解朴素匹配是如何工作的,先看一个例子:

目标串:”abaababba”

模式串:”abab”

第一次匹配
序号	0	1	2	3	4	5	6	7	8
目标串	a	b	a	a	b	a	b	b	a
模式串	a	b	a	b

从这里看出,匹配到目标指针等于3时匹配失败.

朴素的算法是这样处理的:

当匹配失败时，目标指针回退到上一次开始比较的位置的下一位置，模式串指针直接回退到起点：如本例中，目标指针回退到1，模式串指针回到0，好，继续比较：

序号	0	1	2	3	4	5	6	7	8
目标串	a	b	a	a	b	a	b	b	a
模式串		a	b	a	b

 

就这样直到这里匹配成功

序号	0	1	2	3	4	5	6	7	8
目标串	a	b	a	a	b	a	b	b	a
模式串				a	b	a	b

 

2.       朴素算法的改进点

从上面朴素算法看,算法的确可以进行改进,为什么呢?我们看

第二次匹配
序号	0	1	2	3	4	5	6	7	8
目标串	a	b	a	a	b	a	b	b	A
模式串		a	b	a	b

 

这次匹配必须吗？

在上一次的匹配中,是在模式串的第3位才匹配失败的,那么我们知道

T[0,1,2] == P[0,1,2]  -----(1)

下一次匹配时,比较T[1]和P[0],根据式(1),我们知道

T[0] == P[0],所以我们只需要知道P[0]是否等于P[1]就可以确定T[1]是否等于P[0]

这里我们已经知道P[0] == ‘a’,P[1] == ‘b’,P[0] 是不等于P[1]的,所以T[1]不用和P[0]比较

好了,继续看第三次朴素匹配需不需要做:

第三次匹配
序号	0	1	2	3	4	5	6	7	8
目标串	a	b	a	a	b	a	b	B	a
模式串			a	b	a	b

从第一次匹配结果,即式(1),我们知道T[2] == P[3]

这里只需要比较P[0]是否等于P[2],从这里看出是相等的,所以第三次匹配是必要的,这次的匹配从T[3]和P[1]开始,注意到目标串的序号并不会回退

 

所以KMP的动机是：不要让目标指针回退，减少重复比较。

3.       一般性推导

前面有了感性认识后,我们来进行一般性推导

 (1)KMP要解决问题

在第s+1趟匹配中,假如匹配过程在模式串的前j个都匹配成功,即

T[s,(s+1),….(s+j)] == P[0,1,…j] --- (2)

而在P[j+1]时失配,那么该回到模式串的第几个位置开始匹配呢?

 

 

(2)推导

         假设在第j+1时匹配失败，那么有：

 

 

 

 

T和P的关系在上图中清楚看出来了,根据前面的朴素算法的思想,我们会进行这样的试探:

第s+2次匹配(试探)
序号	s	s+1	s+2	s+3	…….	s+j-1	s+j	s+j+1	…
目标串	T[s]	T[s+1]	T[s+2]	T[s+3]	….	T[s+j-1]	T[s+j]	T[s+j+1]
模式串移动前	P[0]	P[1]	P[2]	P[3]	….	P[j-1]	P[j]	P[j+1]
模式串 移动后		P[0]	P[1]	P[2]	….	P[j-2]	P[j-1]

如果有P[0,1,2…j-1] != P[1,2,…j],那么我们知道这个必然是失配的

那么再移一位又怎样？这样我们自然而然去做右移试探:

第s+3次匹配(试探)
序号	s	s+1	s+2	s+3	…….	s+j-1	s+j	s+j+1	…
目标串	T[s]	T[s+1]	T[s+2]	T[s+3]	….	T[s+j-1]	T[s+j]	T[s+j+1]
模式串移动前	P[0]	P[1]	P[2]	P[3]	….	P[j-1]	P[j]	P[j+1]
模式串 移动后			P[0]	P[1]	….	P[j-3]	P[j-2]

这里比较P[0,1,…j-2]和P[2,3…j]

 

整个流程：

 

 

 

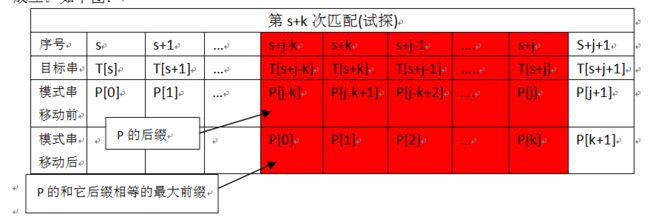
到这里或许你已经看出来了,我们只需要找到一个位置k,使:

P[0,1,2…k] == P[j-k,j-k+1,…..j]

成立。如下图：

 

 

本质：找到一个最大的位置K，使在前一次匹配成功的子模式串的前缀等于它的后缀

故next[j] = k (0<= k < j ),找不到k就表示为-1

 

4.       手工计算

这里举一个例子,来讲next的计算

 

模式串“abababc”

子串长度	子串	Next	说明
1	a	-1	找不到k
2	ab	-1	找不到k
3	aba	0	P[0] = P[2] k==0
4	abab	1	P[0,1] = P[1,2]
5	ababa	2	P[0,1,2] = P[2,3,4]
6	ababab	3	P[0,1,2,3] = P[2,3,4,5]
7	abababc	-1	找不到k

 

5.       程序实现计算next

直接套公式计算是可行,但复杂度较高

用递推的方法做则比较好.

设next(j) = k,则有

P[0,1,2…k] = P[j-k,j-k+1,…j]   ---  (3)

我们来计算next(j+1) = k’

先套定义：P[0,1,2….k’] = P[j-k’,j-k’+1,….j+1]   ---(4)

情况1：

从(3)式看出，如果P[k+1] == P[j+1]，则必有k’ = k+1,即next(j+1) = next(j)+1;

情况2：

如果P[k+1] != P[j+1],那么只能后退找最长前缀了，可以用反证法证明不能前进找。

从式(2)看出，必须找出一个最大h，使：

P[0,1,2…h ] = P[k-h,k-h+1,…k] (即h = next(k))

         这时如果P[h+1] == P[j+1],那么h就是所求，否则按上面步骤一直求直到h = -1(找不到)

         下面给出C++实现代码：

 

void ComputeNext(char *_str,const int _length,int* _next)

{

       _next[0] = -1;

       int k = -1;

 

       //递推求next[j]

       for(int j = 1; j < _length; ++j)

       {

              //P[k+1]和P[j]不等时，一直后退，这里的j、也即文中求的j+1

              while(k >= 0 && _str[k+1] != _str[j])

              {

                     k = _next[k];

              }

              //相等时next = k + 1

              if(_str[k+1] == _str[j])

                     ++k;

              _next[j] = k;

       }

}

 

7.程序实现KMP

//Kmp算法

int FindKmp(char *chSrc,char *pTemplate,int sizeTemplate,int *next)

{

       int pointerToSrc = 0;

       int ponterToTemp = 0;

       size_t lengthSrc = strlen(chSrc);

       while( (ponterToTemp < (int)sizeTemplate) && (pointerToSrc < (int)lengthSrc) )

       {

              //匹配，两指针前进

              if(chSrc[pointerToSrc] == pTemplate[ponterToTemp])

              {

                     ++pointerToSrc;

                     ++ponterToTemp;

              }

              else

              {

                     //不等于-1时模式指针回退

                     if(next[ponterToTemp] != -1)

                            ponterToTemp = next[ponterToTemp];

                     else

                     {

                            //前面已比较的子串已经没有匹配的可能，源指针前进，模式指针归

                            ponterToTemp = 0;

                            ++pointerToSrc;

                     }

              }

       }

       if(ponterToTemp >= (int)sizeTemplate)

              return pointerToSrc - ponterToTemp +1;

       return -1;

}

 

一个KMP的寻找子串的函数如下:

//interface

int FindChildChar(char *chSrc,char *chCmp)

{

       int nLenCmp = strlen(chCmp);

       int *next = new int [nLenCmp];

       if(nLenCmp <= 0)

              return -1;

       computeNext(chCmp,nLenCmp,next);

       int ret  = FindKmp(chSrc,chCmp,nLenCmp,next);

       delete []next;

       return ret;

}

 

参考：

         《算法导论》

         《数据结构-基于C++面向对象》