POJ 3013 Big Christmas Tree(Dijkstra)

POJ 3013 Big Christmas Tree(Dijkstra)

http://poj.org/problem?id=3013

题意:

         给你一个无向图,该图的每个点有一个权重,且每条边有一个单位重量开销.现在要你找出该图的一个以1号节点为根的生成树,且要求该树所有边的开销和最小. 这里每条边的开销 == 该边的单位重量开销 * 该边的子孙节点的权重和(即该边的所有子孙的重量和值).

分析:

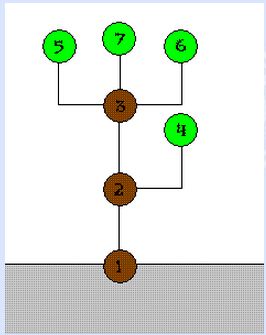
        对于任意一棵生成树,它的开销 == 边的开销之和.或者我们可以换另一种思路来思考这题.对于下面这个生成树:

        它的总开销是多少呢? 我们按边计算可行,现在我们按点计算.对于节点5 因为 节点1要通过边(1,2) ,边(2,3) 边(3,5)来连接5,所以节点5对于整棵树的开销=  5节点的权重*(边(1,2)的单位价格,边(2,3)的单位价格,边(3,5)的单位价格 ) .

        所以其实节点5对于树开销的共享就等于 5节点的重* 1节点到5节点的(最短)路长.其他节点对于整个树开销的贡献也是类似的.

        我们如果要想树的开销最小,只要使得构成生成树的从1节点到其他节点的路径都是最短路径即可.(如果存在孤立点,则No Answer).

AC代码:

#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
#include<queue>
using namespace std;
const int maxn= 50000+10;
int n,m;
int weight[maxn];

struct Edge
{
    int from,to;
    long long dist;
    Edge(int from,int to,long long dist):from(from),to(to),dist(dist){}
};

struct HeapNode
{
    long long d;
    int u;
    HeapNode(long long d,int u):d(d),u(u){}
    bool operator < (const HeapNode &rhs) const
    {
        return d > rhs.d;
    }
};

struct Dijkstra
{
    int n,m;
    vector<Edge> edges;
    vector<int> G[maxn];
    long long d[maxn];
    bool done[maxn];

    void init(int n)
    {
        this->n = n;
        for(int i=0;i<n;i++) G[i].clear();
        edges.clear();
    }

    void AddEdge(int from,int to,long long dist)
    {
        edges.push_back(Edge(from,to,dist));
        m= edges.size();
        G[from].push_back(m-1);
    }

    void dijkstra()
    {
        priority_queue<HeapNode> Q;
        for(int i=0;i<n;i++) d[i]=1e16;
        d[0]=0;
        memset(done,0,sizeof(done));
        Q.push(HeapNode(d[0],0));

        while(!Q.empty())
        {
            HeapNode x= Q.top(); Q.pop();
            int u=x.u;
            if(done[u]) continue;
            done[u]=true;

            for(int i=0;i<G[u].size();i++)
            {
                Edge &e=edges[G[u][i]];
                if(d[e.to] > d[u]+e.dist)
                {
                    d[e.to] = d[u]+e.dist;
                    Q.push(HeapNode(d[e.to],e.to));
                }
            }
        }
    }
}DJ;

int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d",&n,&m);
        DJ.init(n);
        for(int i=0;i<n;i++)
            scanf("%d",&weight[i]);
        for(int i=0;i<m;i++)
        {
            int u,v,d;
            scanf("%d%d%d",&u,&v,&d);
            u--,v--;
            DJ.AddEdge(u,v,d);
            DJ.AddEdge(v,u,d);
        }
        DJ.dijkstra();

        long long min_val=0;
        bool ok=true;
        for(int i=0;i<n;i++)
        {
            if(DJ.d[i]== 1e16)
            {
                ok=false;
                break;
            }
            min_val += DJ.d[i]*weight[i];
        }
        if(ok)  printf("%I64d\n",min_val);
        else    printf("No Answer\n");
    }
    return 0;
}